Рассмотренные методы линейного программирования успешно применяются для решения задач большой размерности при ограничениях, записанных как в виде равенств, так и в виде неравенств. Способ решения задач нелинейного программирования с помощью процедуры, использующей линеаризацию только ограничений, оставляя целевую функцию нелинейной на всех этапах минимизации, используется в методе обобщенного приведенного градиента. Структура данного метода предполагает реализацию (по отношению к нелинейным функциям) линейно-аппроксимирующих процедур; определение новых переменных, ортогональных к некоторым ограничениям; приведение градиента целевой функции к преобразованному таким способом базису. В оптимизационной схеме могут использоваться ограничения в виде неравенств.
Методом приведенного градиента решаются задачи минимизации функции
j(х), где хÎEn, (2.4.1)
при ограничениях в виде равенств:
hi (x) = 0, i = 1,..., m (2.4.2)
и ограничениях в виде неравенств:
Lj£gj (x) £Uj, j = 1,..., k. (2.4.3)
Ограничения в виде неравенств (2.4.3) удается включить в оптимизационную схему путем вычитания из левых частей ограничений неотрицательных переменных, что превращает ограничения-неравенства в ограничения-равенства вида:
hi (x) = gi (x) - vi2 = 0 (2.4.4)
где - ¥£vi£¥
Переменные vi добавляются к n переменным исходной задачи.
Различают две системы переменных: m базисных (зависимых) переменных xi и (n - m) небазисных (независимых) переменных хК. При этом зависимые переменные определяются через независимые переменные. Следовательно, функция j(х) есть функция лишь (n - m) независимых переменных. Уравнения задающие ограничения не могут быть разрешены относительно зависимых переменных.
Задача оптимизации функции j(х) методом приведенного градиента решается следующим образом.
Пусть требуется минимизировать функцию j(х1, х2) при ограничении hi(х1, х2) = 0, (i = 1,..., m). При бесконечных малых приращения х1 и х2 имеем:
dj (х1, х2) = 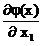 dx1 +
dx1 + 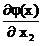 dx2. (2.4.5)
dx2. (2.4.5)
Кроме того,
dh(х1, х2) = 
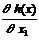 dx1 +
dx1 + 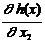 dx2 = 0. (2.4.6)
dx2 = 0. (2.4.6)
Выражения (2.4.5) и (2.4.6) линейны относительно dx1 и dx2. Поэтому из выражения (2.4.5) либо dx1, либо dx2 можно исключить. Единственнодопустимым перемещением является перемещение вдоль ограничения:dh(х1, х2) = 0.
Решим уравнение dh(х1, х2) =0 относительно dx2:
dx2 = - 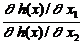 dx1.(2.4.7)
dx1.(2.4.7)
Полученное решение подставим в выражение (2.4.5)
dj (х1, х2) =(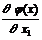 -
- 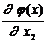 ´
´ 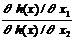 ) dx1.(2.4.8)
) dx1.(2.4.8)
Отсюда получим выражение для приведенного градиента:
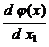 =
= 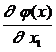 -
- 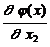 ´
´ 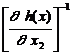 ´
´ 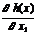 (2.4.9)
(2.4.9)
Обозначим компоненты градиента целевой функции через ÑТХ1j = 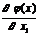 и ÑТХ2 j =
и ÑТХ2 j = 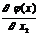 . Тогда выражение (2.4.9) записывается в форме:
. Тогда выражение (2.4.9) записывается в форме:
Ñj = 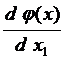 = ÑТХ1j - ÑТХ2 j´
= ÑТХ1j - ÑТХ2 j´ 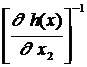 ´
´ 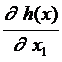 . (2.4.10)
. (2.4.10)
Выражение (2.4.10) в общем случае имеет вид:
Ñj = 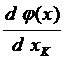 = ÑТХК j - ÑТХMj´
= ÑТХК j - ÑТХMj´ 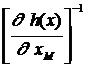 ´
´ 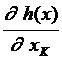 , (2.4.11)
, (2.4.11)
где
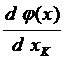 =
= 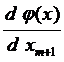 ...
... 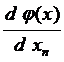 – [1 ´ (n - m)] – мерная матрица
– [1 ´ (n - m)] – мерная матрица
(матрица приведенного градиента),
ÑТХMj = 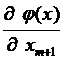 ...
... 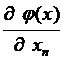 – [1 ´ (n - m)] –мерная матрица,
– [1 ´ (n - m)] –мерная матрица,
ÑТХКj = 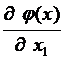 ...
... 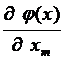 – (1 ´ m) –мерная матрица,
– (1 ´ m) –мерная матрица,
h = 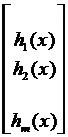 – (m ´ 1) –мерная матрица,
– (m ´ 1) –мерная матрица,
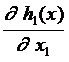 ...
... 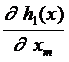
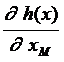 = – m ´m –мерная квадратная матрица («базисная» матрица),
= – m ´m –мерная квадратная матрица («базисная» матрица),
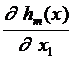 ...
... 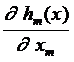
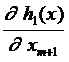 ...
... 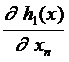
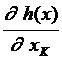 = [m ´ (n - m)] –мерная матрица.
= [m ´ (n - m)] –мерная матрица.
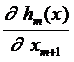 ...
... 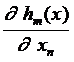
Следует отметить, что число составляющих вектора приведенного градиента Ñj равняется числу независимых переменных.
Алгоритм обобщенного приведенного градиента начинает работать с начальной точки 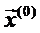 . Значения составляющих приведенного градиента z(K)=
. Значения составляющих приведенного градиента z(K)= 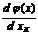 служат ориентиром при отыскании оптимального вектора
служат ориентиром при отыскании оптимального вектора 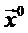 . Направления оптимизационного поиска Dj(K) (j=m+1,..., n), соответствующие независимым переменным, через значения составляющих приведенного градиента определяются следующим образом:
. Направления оптимизационного поиска Dj(K) (j=m+1,..., n), соответствующие независимым переменным, через значения составляющих приведенного градиента определяются следующим образом:
если хj(K) = Uj и zj(K) > 0,
Dj(K) = 0 (2.4.12)
если хj(K) = Lj и zj(K) < 0,
Dj(K) = - zj(K), если Lj<хj(K) <Uj (2.4.13)
Поиск состоит в отыскании точки, в которой приведенный градиент целевой функции Ñj обращается в нуль.



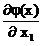 dx1 +
dx1 + 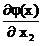 dx2. (2.4.5)
dx2. (2.4.5)
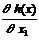 dx1 +
dx1 + 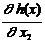 dx2 = 0. (2.4.6)
dx2 = 0. (2.4.6)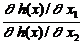 dx1.(2.4.7)
dx1.(2.4.7)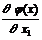 -
- 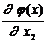 ´
´ 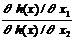 ) dx1.(2.4.8)
) dx1.(2.4.8)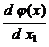 =
= 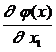 -
- 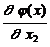 ´
´ 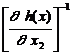 ´
´ 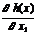 (2.4.9)
(2.4.9)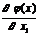 и ÑТХ2 j =
и ÑТХ2 j = 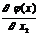 . Тогда выражение (2.4.9) записывается в форме:
. Тогда выражение (2.4.9) записывается в форме: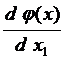 = ÑТХ1j - ÑТХ2 j´
= ÑТХ1j - ÑТХ2 j´ 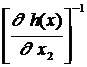 ´
´ 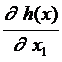 . (2.4.10)
. (2.4.10)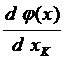 = ÑТХК j - ÑТХMj´
= ÑТХК j - ÑТХMj´ 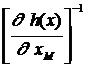 ´
´ 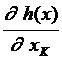 , (2.4.11)
, (2.4.11)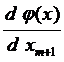 ...
... 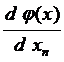 – [1 ´ (n - m)] – мерная матрица
– [1 ´ (n - m)] – мерная матрица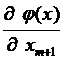 ...
... 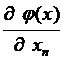 – [1 ´ (n - m)] –мерная матрица,
– [1 ´ (n - m)] –мерная матрица,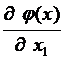 ...
... 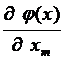 – (1 ´ m) –мерная матрица,
– (1 ´ m) –мерная матрица,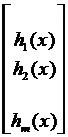 – (m ´ 1) –мерная матрица,
– (m ´ 1) –мерная матрица,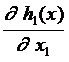 ...
... 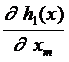
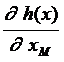 = – m ´m –мерная квадратная матрица («базисная» матрица),
= – m ´m –мерная квадратная матрица («базисная» матрица),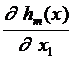 ...
... 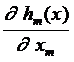
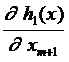 ...
... 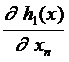
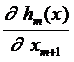 ...
... 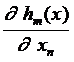
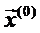 . Значения составляющих приведенного градиента z(K)=
. Значения составляющих приведенного градиента z(K)= 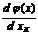 служат ориентиром при отыскании оптимального вектора
служат ориентиром при отыскании оптимального вектора 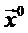 . Направления оптимизационного поиска Dj(K) (j=m+1,..., n), соответствующие независимым переменным, через значения составляющих приведенного градиента определяются следующим образом:
. Направления оптимизационного поиска Dj(K) (j=m+1,..., n), соответствующие независимым переменным, через значения составляющих приведенного градиента определяются следующим образом:


