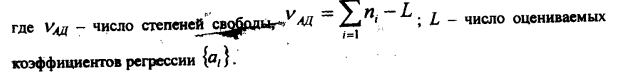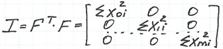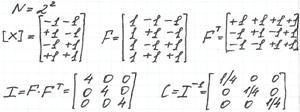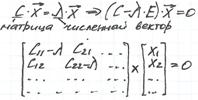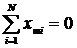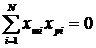6. Дисперсионный анализ опытных данных 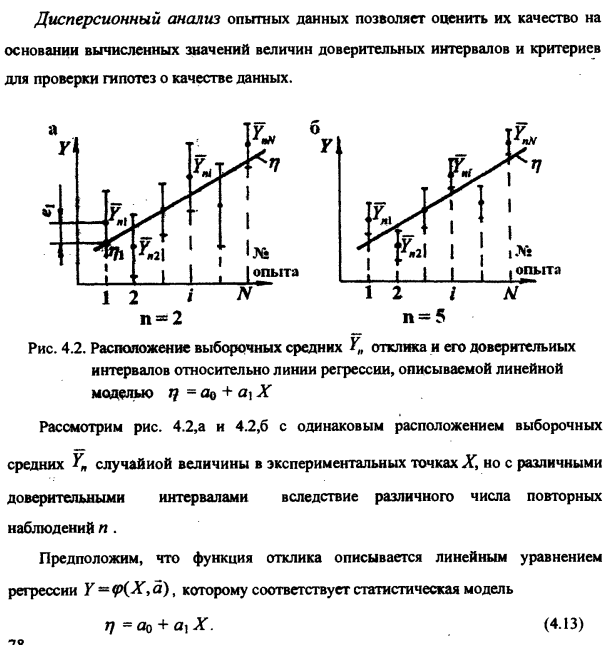

7. Основные понятия и определения планирования эксперимента
Планирование эксперимента – процедура выбора количества экспериментов и условий их проведения, необходимых для решения поставленной задачи с требуемой точностью.
Факторами называются величины, которые экспериментатор изменяет по своему усмотрению. Факторы – вектора.

I=FT∙F – информационная матрица плана [x]. C=I-1 – ковариационная матрица плана [x]/
План эксперимента называется ортогональным, если информационная матрица диагональная
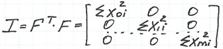
Ортогональные планы используются, когда точный вид модели неизвестен и исследователь использует данные для отбора переменных, которые существенно влияют на выходную величину.
План называется центральным, если его центр расположен в начале координат.
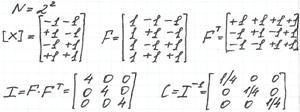
Матрица I – диагональная => план ортогональный.

Композитностью плана называется свойство плана, позволяющее разделить эксперимент на несколько этапов и постепенно переходить от простых моделей к более сложным, используя предыдущие наблюдения.
Насыщенность плана – связь между количеством факторов М и опытов N, если N<M, то нельзя найти ед. значения коэффициентов модели [ae].
Критерий оптимальности плана.
1-я группа – следит за точностью экспериментов модели. [ae] – оценивает точность коэффициентов модели. D, A, E – оптимальность.
2-я группа – оценивает точность предсказания по модели η. G, Q – оптимальность.
3-я группа – связана со стратегией эксперимента
Коэффициенты модели случайной величины имеют доверительный интервал.
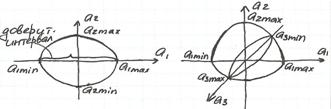
D – оптимальные планы – называются планы, которые соответствуют min определителю по ковариационной матрице.
С=I-1=(FT∙F)-1
min|c|
Определитель ковариационной матрицы пропорционален объему эллипсоида рассеивания коэф. модели.
А – оптимальные планы – это планы, которым соответствует минимальный след ковариационной матрицы.

(след): SpurC=С11+С22+С33+СLL
А – оптимальные планы обеспечивают минимум средней дисперсии коэффициентов модели.
Е – оптимальный план – соответствует собственному значению ковариационной матрицы.
λ – собственное значение матрицы С. Система уравнений С∙x, в этой системе матрицу можно заменить числом, расположенным по диагонали – это собственное значение матрицы.
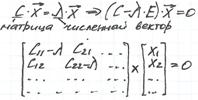
Е – оптимальные планы не позволяют дисперсиям отдельных коэффициентов моделей иметь недопустимо большие размеры.
G – оптимальные планы – минимизируют максимально возможную дисперсию предсказания от модели: min (maxD(η)). Эти планы гарантируют, что в области эксперимента нет точек, которые имеют низкую точность вычисления по модели.
Q – оптимальные планы – минимизируют среднюю дисперсию предсказания. minDcp(η), Dcp – средняя дисперсия.
Построить планы, удовлетворяющие одновременно нескольким критериям оптимальности можно только для простых моделей, поэтому используют планы, построенные на компромиссном решении, близкие к оптимальным планам по разным критериям. Такие планы называются робастные планы.
е(D), е(A), е(E), е(Q) и т.д. – коэффициенты. Чем ближе произв. план к оптимальному оценивают коэффициенты е.
План полного факторного эксперимента
Планирование эксперимента – процедура выбора количества экспериментов и условий их проведения, необходимых для решения поставленной задачи с требуемой точностью.
Факторами называются величины, которые экспериментатор изменяет по своему усмотрению. Факторы – вектора.
Полным факторным экспериментом называется эксперимент, при котором реализуются все возможные сочетания уровней варьирования.
Свойства полного факторного плана эксперимента.
1. Симметричность относительно центра эксперимента: Алгебраическая сумма элементов вектора столбца каждого фактора равна нулю.
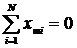
2. Ортогональность матрицы планирования: Сумма произведений элементов любых двух векторных столбцов равна нулю.
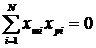
3. Условие нормировки: Сумма квадратов элементов столбца каждого фактора равна количеству опытов.

4. Точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления
9. Классификация планов эксперимента
Планирование эксперимента – процедура выбора количества экспериментов и условий их проведения, необходимых для решения поставленной задачи с требуемой точностью.
Факторами называются величины, которые экспериментатор изменяет по своему усмотрению. Факторы – вектора.

I=FT∙F – информационная матрица плана [x]. C=I-1 – ковариационная матрица плана [x]/
План эксперимента называется ортогональным, если информационная матрица диагональная
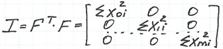
Ортогональные планы используются, когда точный вид модели неизвестен и исследователь использует данные для отбора переменных, которые существенно влияют на выходную величину.
План называется центральным, если его центр расположен в начале координат.
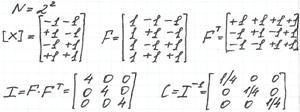
Матрица I – диагональная => план ортогональный.

Композитностью плана называется свойство плана, позволяющее разделить эксперимент на несколько этапов и постепенно переходить от простых моделей к более сложным, используя предыдущие наблюдения.
Насыщенность плана – связь между количеством факторов М и опытов N, если N<M, то нельзя найти ед. значения коэффициентов модели [ae].
Критерий оптимальности плана.
1-я группа – следит за точностью экспериментов модели. [ae] – оценивает точность коэффициентов модели. D, A, E – оптимальность.
2-я группа – оценивает точность предсказания по модели η. G, Q – оптимальность.
3-я группа – связана со стратегией эксперимента
Коэффициенты модели случайной величины имеют доверительный интервал.

D – оптимальные планы – называются планы, которые соответствуют min определителю по ковариационной матрице.
С=I-1=(FT∙F)-1
min|c|
Определитель ковариационной матрицы пропорционален объему эллипсоида рассеивания коэф. модели.
А – оптимальные планы – это планы, которым соответствует минимальный след ковариационной матрицы.

(след): SpurC=С11+С22+С33+СLL
А – оптимальные планы обеспечивают минимум средней дисперсии коэффициентов модели.
Е – оптимальный план – соответствует собственному значению ковариационной матрицы.
λ – собственное значение матрицы С. Система уравнений С∙x, в этой системе матрицу можно заменить числом, расположенным по диагонали – это собственное значение матрицы.
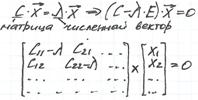
Е – оптимальные планы не позволяют дисперсиям отдельных коэффициентов моделей иметь недопустимо большие размеры.
G – оптимальные планы – минимизируют максимально возможную дисперсию предсказания от модели: min (maxD(η)). Эти планы гарантируют, что в области эксперимента нет точек, которые имеют низкую точность вычисления по модели.
Q – оптимальные планы – минимизируют среднюю дисперсию предсказания. minDcp(η), Dcp – средняя дисперсия.
Построить планы, удовлетворяющие одновременно нескольким критериям оптимальности можно только для простых моделей, поэтому используют планы, построенные на компромиссном решении, близкие к оптимальным планам по разным критериям. Такие планы называются робастные планы.
е(D), е(A), е(E), е(Q) и т.д. – коэффициенты. Чем ближе произв. план к оптимальному оценивают коэффициенты е.
10. Критерии оптимальности планов эксперимента.





11. Построение линейных и квазилинейных уравнений регрессии на базе планирования эксперимента