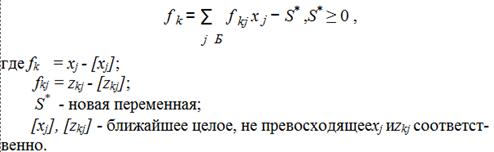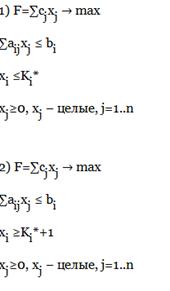Последовательный симплексный метод относится к методам поиска экстремума целевой функции, применение которого требует проведения минимально возможного числа опытов при определении направления движения.
Симплексом называется простейшая выпуклая геометрическая фигура. Под n–мерным симплексом понимают фигуру, образованную множеством (n+1) точек. Эти точки называются вершинами симплекса. В двухмерном пространстве симплексом является треугольник, в трехмерном пространстве - тетраэдр.
Симплекс называется регулярным, если расстояние между всеми точками, образующими симплекс, одинаковы. Из произвольного симплекса всегда можно получить регулярный путем преобразования системы координат. В симплексном методе оптимизации будем использовать только регулярные симплексы.
Начальный симплекс может быть построен двумя способами: с вершиной в начале координат и с центром в начале координат.
Таблица 2.2.1.Координаты вершин симплекса с вершиной в начале координат
| Номер вершины
i
| Координаты вершин симплекса
|
| Х1
| Х2
| Х3
| …
| Хn
|
|
…
n+1
|
p
g
g
…
g
|
g
p
g
…
g
|
g
g
p
…
g
| …
…
…
…
…
…
|
g
g
g
…
p
|
Симплекс целесообразно использовать в нормированном виде, т.е. с длиной ребер равной единице. При единичной длине ребра симплекса значения p и g равны:
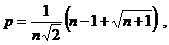
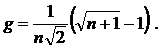 (2.2.1)
(2.2.1)
Координаты вершин симплекса с центром в начале координат приведены в матрице табл. 2.2.2, где обозначены:
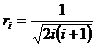 ,
, 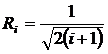 . (2.2.2)
. (2.2.2)
Изменение каждого управляющего параметра на единицу приводит приблизительно к одинаковому изменению целевой функции.
Таблица 2.2.2. Координаты вершин симплекса с центром в начале координат
| Номер вершиныi
| Координаты вершин симплекса
|
| Х1
| Х2
| Х3
| …
| Хn
|
|
…
n+1
| -r1
R1
…
| -r2
-r2
R2
…
| -r3
-r3
-r3
R3
…
| …
…
…
…
…
…
| -rn
-rn
-rn
-rn
…
Rn
|
Экспериментальное определение оптимума целевой функции осуществляется с помощью следующей процедуры:
1. Вычисляются координаты начального симплекса.
2. Отбрасывается точка плана с наихудшим значением целевой функции и строится новый симплекс. Новый симплекс образуется оставшимися вершинами исходного симплекса и новой вершиной, получаемой путем зеркального отображения отброшенной вершины относительно противоположной грани исходного симплекса.
Координаты новой точки в векторной форме определяются по следующей формуле:
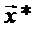 =
= 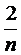
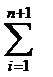
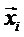 - (
- (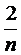 + 1)
+ 1) 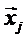 , (2.2.3)
, (2.2.3)
где j– номер вершины исходного симплекса с наихудшим значением целевой функции.
Прогнозируемое значение целевой функции в новой точке равно:
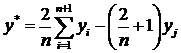 . (2.2.4)
. (2.2.4)
3. В новой точке 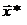 проводится эксперимент, и получают соответствующее значение целевой величины y*.
проводится эксперимент, и получают соответствующее значение целевой величины y*.
4. Симплекс последовательно перемещается. На каждом шаге происходит отбрасывание вершины симплекса с наихудшим значением целевой функции и реализуется опыт в новой вершине.
5. Оптимум считается достигнутым, если одна и та же точка входит в последовательные симплексы n раз и выполняется условие:
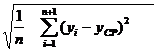 £f, (2.2.5)
£f, (2.2.5)
где f– принятое допустимое значение, yСР– среднее значение целевой функции в вершинах симплекса.
Геометрическая интерпретация симплексного метода показана на рис. 2.2.1. Основными преимуществами последовательного симплексного метода являются слабая чувствительность к форме минимизируемой поверхности и повышение эффективности метода с увеличением числа факторов. Однако метод не дает информации о влиянии каждого фактора на целевую функцию.
7. Методы решения задач с нецелочисленным планом
Существует ряд задач оптимального планирования, в которых переменные могут принимать лишь целочисленные значения. Такие задачи связаны с определением количества единиц неделимой продукции, числа станков при загрузке оборудования, численности работников в структурных подразделениях предприятия и т.д. Достаточно часто возникают задачи с так называемыми булевыми переменными, решениями которых являются суждения типа «да-нет». Если функция и ограничения в таких задачах линейны, то мы говорим о задаче линейного целочисленного программирования.
Задача линейного целочисленного программирования формулируется следующим образом: найти такое решение (план)
Х = (x1, x2,..., xn),

Метод Гомори
Сущность метода заключается в построении ограничений, отсекающих нецелочисленные решения задачи линейного программирования, но не отсекающих ни одного целочисленного плана.
1.Решаем задачу симплексным методом без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования. Если обнаруживается неразрешимость задачи, то и неразрешима задача целочисленного программирования.
2.Если среди компонент оптимального решения есть нецелые, то к ограничениям задачи добавляем новое ограничение, обладающее следующими свойствами:
- оно должно быть линейным;
- должно отсекать найденный оптимальный нецелочисленный план;
- не должно отсекать ни одного целочисленного плана.
Для построения ограничения выбираем компоненту оптимального плана с наибольшей дробной частью и по соответствующей этой компоненте k-й строке симплексной таблицы записываем ограничение Гомори.
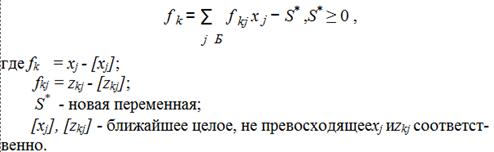

4. Решаем при помощи обычных симплексных преобразований полученную задачу. Если решение этой задачи приводит к целочисленному оптимальному плану, то искомая задача решена. Если мы получили нецелочисленное решение, то снова добавляем одно дополнительное ограничение, и процесс вычислений повторяется. Проделав конечное число итераций, либо получаем оптимальный план задачи целочисленного программирования, либо устанавливаем ее неразрешимость.
Замечания:
1.Если дополнительная переменная S* вошла в базис, то после пересчетакакого-либопоследующего плана соответствующие ей строку и столбец можно удалить (тем самым сокращается размерность задачи).
2.Если для дробного xj обнаружится целочисленность всех коэффициентов соответствующего уравнения (строки), то задача не имеет целочисленного решения.
Метод ветвей и границ
Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи.
Метод ветвей и границ основан на предположении, что новый оптимальный нецелочисленный план дает значение функции, большее, чем всякий последующий план перехода.
Пусть переменная xi в плане дробное число. Тогда в оптимальном план ее значение будет, по крайней мере: либо меньше или равно ближайшему меньшему целому числу Ki*; либо больше или равно ближайшему большему целому числу Ki*.
Определяя эти числа симплексным методом решения двух ЗЛП:
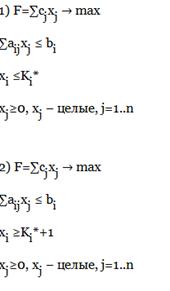
Возможны четыре случая при решении этой пары задач:
1) Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции и дают решение исходной задачи.
2) Одна из задач неразрешима, а другая имеет нецелочисленный оптимальный план. Тогда рассматривается вторая задача и в ее оптимальном плане выбирается одна из компонент, значение которой равно дробному числу и строятся две новые задача, аналогично предыдущим.
3) Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значение целевой функции от планов и сравниваем их между собой. Если на целочисленном оптимальном план значение целевой функции больше или равно ее значению в плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и дает искомое решение.
4)Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда рассматриваем ту из задач, для которой значение целевой функции является наибольшим. Строятся новые две задачи.
Алгоритм метода ветвей и границ
1. Находится решение задачи линейного программирования без учета целочисленности.
2. Составляется дополнительные ограничения на дробную компоненту плана.
3. Находится решение двух задач с ограничениями на компоненту.
4. Строятся в случае необходимости дополнительные ограничения, согласно возможным четырем случаям. Определяется оптимальный целочисленный план, либо устанавливается неразрешимость задачи.



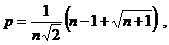
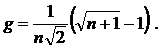 (2.2.1)
(2.2.1)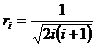 ,
, 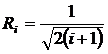 . (2.2.2)
. (2.2.2)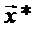 =
= 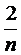
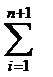
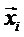 - (
- (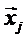 , (2.2.3)
, (2.2.3)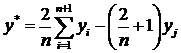 . (2.2.4)
. (2.2.4)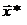 проводится эксперимент, и получают соответствующее значение целевой величины y*.
проводится эксперимент, и получают соответствующее значение целевой величины y*.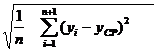 £f, (2.2.5)
£f, (2.2.5)