Ознакомьтесь с теорией в конспекте и в учебниках 1. Трофимова Т.И. Курс физики. Гл.8. §43, 44, 46. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл.10, §10.1, 10.2, 10.3, 10.6. Выберите «Термодинамика и молекулярная физика» и «Кинетическая модель идеального газа». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите основные сведения в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
ЦЕЛЬ РАБОТЫ:
· Знакомство с компьютерной моделью идеального газа.
· Экспериментальное подтверждение основных формул молекулярно-кинетической теории, по которым определяются скорости газовых молекул.
· Экспериментальное изучение зависимостей среднего числа столкновений и средней длины свободного пробега молекул от температуры.
КРАТКАЯ ТЕОРИЯ:
ИДЕАЛЬНЫМ ГАЗОМ называется физическая модель, в которой газ рассматривается как совокупность хаотически движущихся молекул, взаимодействующих между собой лишь при непосредственном ударе, носящем упругий характер.
Скорости, характеризующие состояние идеального газа:
1. средняя: 
 ;
;  (1)
(1)
2..наиболее вероятная: vв =  =
=  ; (2)
; (2)
3. средняя квадратичная:  . (3)
. (3)
Давление газа - макроскопическое проявление теплового движения и столкновений молекул газа со стенками сосуда. В результате каждого соударения стенке сосуда передаётся определённый импульс.
ОСНОВНОЕ УРАВНЕНИЕ молекулярно-кинетической теории для давления: р =  . (4)
. (4)
ДЛИНА СВОБОДНОГО ПРОБЕГА - расстояние li, которое молекула пролетает от одного столкновения до следующего.
СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ:
 =
=  . (5)
. (5)
СРЕДНЕЕ ЧИСЛО СОУДАРЕНИЙ МОЛЕКУЛЫ В ЕДЕНИЦУ ВРЕМЕНИ:
 (6)
(6)
МЕТОДИКА ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ.

Нажмите кнопку «СТАРТ» во внутреннем окне экрана и проследите за хаотическим движением выделенной молекулы в замкнутом объёме слева во внутреннем окне экрана, вектор скорости которой изменяется при каждом упругом соударении с другими молекулами (их около 100) и со стенками сосуда. Данная молекулярная система является «механической» моделью идеального газа, находящегося при достаточно низком давлении. В правой части внутреннего окна происходит непрерывная регистрация ломаной линии – траектории движения выделенной молекулы - состоящей из отдельных длин свободного пробега молекулы.









 В процессе исследований можно в любой момент времени остановить движение всех молекул нажатием кнопки;, расположенной в правом верхнем углу внешнего окна опыта, и получить «мгновенную фотографию» всех молекул газа и траектории движения выделенной частицы. Продолжить наблюдение движения молекул в непрерывном режиме можно нажатием кнопки 8 или в «пошаговом» режиме последовательными нажатиями кнопки4. Обе кнопки расположены рядом.
В процессе исследований можно в любой момент времени остановить движение всех молекул нажатием кнопки;, расположенной в правом верхнем углу внешнего окна опыта, и получить «мгновенную фотографию» всех молекул газа и траектории движения выделенной частицы. Продолжить наблюдение движения молекул в непрерывном режиме можно нажатием кнопки 8 или в «пошаговом» режиме последовательными нажатиями кнопки4. Обе кнопки расположены рядом.
ЭКСПЕРИМЕНТ 1. Исследование зависимости скоростей газовых молекул от температуры
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА:
1.На мониторе щёлкните мышью кнопку «;» в верхнем ряду кнопок.
2. В нижнем внутреннем окне щёлкните мышью кнопку «ОЧИСТИТЬ» и установите с помощью маркера мыши на термометре температуру 100К.
3. Запишите в табл.1 начальное значение скорости (v 1) выделенной молекулы, указанное в нижнем прямоугольнике окна опыта.
4. Отдельными отрывистыми щелчками нажимайте мышью кнопку 4до момента соударения выделенной молекулы с любой другой движущейся молекулой и изменения скорости выделенной молекулы.
5. Запишите в табл.1 второе значение скорости.
6. Продолжите действия по п.4, 5 ещё 18 раз и заполните табл.1.
7. Увеличивая последовательно температуру на 50К, проведите аналогичные измерения скоростей для температур 150К, 200К, 250К, 300К, 350К, 400К, 450К, 500К и заполните табл.2-9.
8. По формулам  (7) и
(7) и  (8) для каждого значения температуры рассчитайте среднюю арифметическую и среднюю квадратичную скорости газовых молекул и запишите эти величины в табл. 10.
(8) для каждого значения температуры рассчитайте среднюю арифметическую и среднюю квадратичную скорости газовых молекул и запишите эти величины в табл. 10.
9. Постройте графики  и
и  , по ним определите значение массы молекулы m0:
, по ним определите значение массы молекулы m0:
 (9)
(9)  (10)
(10)
10. Определите химическую формулу газа, масса молекулы которого наиболее близка к измеренной массе молекулы.
11. Оцените погрешность проведённых измерений массы молекулы.
ТАБЛИЦЫ 1-9. Результаты измерений скорости молекулы при заданной температуре
Т=100…….500К
| №
опыта
|
|
|
|
|
|
|
|
|
|
|
| vi,м/с
|
|
|
|
|
|
|
|
|
|
|
| №
опыта
|
|
|
|
|
|
|
|
|
|
|
| vi, м/с
|
|
|
|
|
|
|
|
|
|
|
ТАБЛИЦА 10. Результаты расчёта скоростей молекул
ЭКСПЕРИМЕНТ 2. Исследование зависимости среднего импульса, передаваемого молекулами при соударении стенкам сосуда, от температуры
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА:
1.На мониторе щёлкните мышью кнопку;в верхнем ряду кнопок.
2. В нижнем ряду кнопок щёлкните мышью кнопку «ОЧИСТИТЬ» и установите с помощью маркера мыши на термометре температуру 100К.
3. В момент начала отсчёта времени на секундомере щёлкните мышью на мониторе в верхнем ряду кнопку 8 и через 1 мин. остановите движение молекул нажатием кнопки;.
4. На «моментальной фотографии» траектории движения выделенной частицы подсчитайте N – число ударов этой молекулы о стенки сосуда за одну минуту. Повторите это измерение ещё 2 раза и запишите результаты измерений в табл.11.
5. Увеличивая последовательно температуру на 50К, проведите аналогичные измерения N для температур в интервале 100- 500К и запишите все результаты измерений в табл.11.
6. По формуле  рассчитайте среднее значение импульса, передаваемого молекулами при соударении стенкам сосуда для каждого значения температуры. Значения m0 и
рассчитайте среднее значение импульса, передаваемого молекулами при соударении стенкам сосуда для каждого значения температуры. Значения m0 и  возьмите из данных опыта 1.
возьмите из данных опыта 1.
7. Постройте по данным таблицы 11 график  = f(T) и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
= f(T) и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
ТАБЛИЦА 11. Результаты измерений числа соударений молекулы о стенки сосуда за 1 мин.
| Т,К
|
|
|
|
|
|
|
|
|
|
| N1
|
|
|
|
|
|
|
|
|
|
| N2
|
|
|
|
|
|
|
|
|
|
| N3
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
ЭКСПЕРИМЕНТ 3. Исследование зависимости средней частоты взаимных столкновений молекул от температуры
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА:
1.На мониторе щёлкните мышью кнопку;в верхнем ряду кнопок.
2. В нижнем ряду кнопок щёлкните мышью кнопку «ОЧИСТИТЬ» и установите с помощью маркера мыши на термометре температуру 100К.
3. В момент начала отсчёта времени на секундомере щёлкните мышью на мониторе в верхнем ряду кнопку 8 и через 30с остановите движение молекул нажатием кнопки;.
4. На «моментальной фотографии» траектории движения выделенной частицы подсчитайте Z – число её взаимных соударений с другими молекулами.
Повторите это измерение ещё 2 раза и запишите результаты измерений в табл.12.
5. Увеличивая последовательно температуру на 50К, проведите аналогичные измерения Z для температур в интервале 100- 500К и запишите все результаты измерений в табл.12.
6. По данным таблицы 12 постройте график зависимости  и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
ТАБЛИЦА 12. Результаты измерений числа взаимных столкновений молекул
| Т,К
|
|
|
|
|
|
|
|
|
|
| Z1
|
|
|
|
|
|
|
|
|
|
| Z2
|
|
|
|
|
|
|
|
|
|
| Z3
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
ЭКСПЕРИМЕНТ 4. Исследование зависимости средней длины свободного пробега молекул от температуры
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА:
1.На мониторе щёлкните мышью кнопку;в верхнем ряду кнопок.
2. В нижнем ряду кнопок щёлкните мышью кнопку «ОЧИСТИТЬ» и установите с помощью маркера мыши на термометре температуру 100К.
3. В момент начала отсчёта времени на секундомере щёлкните мышью на мониторе в верхнем ряду кнопку 8 и через 30с остановите движение молекул нажатием кнопки;.
4. С помощью миллиметровой линейки измерьте на экране монитора все отрезки li ломаной линии – траектории движения выделенной молекулы - от одного столкновения до последующего. При этом имейте в виду, что изменения направления движения молекулы при её ударах о стенки сосуда не должны учитываться при измерении длины свободного пробега.
5. Повторите это измерение ещё 2 раза и запишите результаты измерений в табл.13.
5. Увеличивая последовательно температуру на 50К, проведите аналогичные измерения li для температур в интервале 100- 500К и запишите все результаты измерений в табл.13.
6. По данным таблицы 13 постройте график зависимости  и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
Вопросы и задания для самоконтроля
1. Перечислите основные положения молекулярно- кинетической теории идеального газа.
2. Чем обусловлено давление газа с точки зрения молекулярно-кинетической теории?
3. Зависит ли давление газа: а) от плотности газа; б) от температуры; в) от массы молекул?
4. Как изменяются при изотермическом расширении идеального газа: а) средняя кинетическая энергия молекул; б) средняя длина свободного пробега молекул?
5. Как изменяется средняя длина свободного пробега молекул газа: а) при изобарном нагревании; б) при изотермическом увеличении давления?
6. Что называется эффективным диаметром молекулы?
7. Выведите уравнение, связывающее давление идеального газа со средней кинетической энергией его молекул.
8. Сравните изменения числа ударов молекул о стенку сосуда в единицу времени при уменьшении объёма идеального газа в изотермическом и адиабатическом процессах.
9. Как изменяется эффективный диаметр молекулы при увеличении температуры?
10. Как сказывается ограниченное число молекул, участвующих в тепловом движении в компьютерной модели опыта, на его результатах?
ЛАБОРАТОРНАЯ РАБОТА № 7
ПОЛИТРОПИЧЕСКИЙ ПРОЦЕСС
Ознакомьтесь с теорией в конспекте и в учебниках 1. Трофимова Т.И. Курс физики. Гл.9, §55. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл.9, §9.6. Выберите «Термодинамика и молекулярная физика» и «Работа газа». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите основные сведения в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
ЦЕЛЬ РАБОТЫ:
· Ознакомление с основами анализа и моделирования термодинамических процессов в идеальных газах.
· Определение молярной теплоёмкости в политропических процессах идеального газа.
· Определение показателя адиабаты и работы газа в политропическом процессе.
КРАТКАЯ ТЕОРИЯ:
ПОЛИТРОПНЫМ называется процесс, в котором молярная теплоёмкость С остаётся постоянной. Уравнение политропического процесса имеет вид:
рV n = const, (1)
где n =  . (2)
. (2)
МОЛЯРНОЙ ТЕПЛОЁМКОСТЬЮ называется физическая величина С, численно равная теплоте  , которую нужно сообщить одному молю вещества для изменения его температуры на 1К в рассматриваемом термодинамическом процессе:
, которую нужно сообщить одному молю вещества для изменения его температуры на 1К в рассматриваемом термодинамическом процессе:
С =  , (3) (M - молярная масса, m - масса газа).
, (3) (M - молярная масса, m - масса газа).
Выражение (3) теперь можно записать в форме
 . (4)
. (4)
или в интегральной форме  .
.
Таким образом, если количество тепла, полученное в некотором термодинамическом процессе 1®2 при m = const, прямо пропорционально разности температур 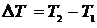 , то теплоёмкость газа постоянна и процесс является политропическим.
, то теплоёмкость газа постоянна и процесс является политропическим.
 .
.
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ для любого равновесного процесса изменения состояния идеального газа имеет вид
 . (5)
. (5)
Тогда из уравнения (5) имеем: C = Cv +  . (6)
. (6)
Связь между объёмом газа и его температурой в политропном процессе можно найти из выражения (1) и уравнения Клапейрона – Менделеева
 :
:
 .
.
Дифференцируя последнее выражение, получим:
 ,
,
 .
.
Тогда уравнение (6) примет вид:
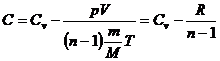 .
.
Учитывая, что  , где
, где  показатель адиабаты, получим:
показатель адиабаты, получим:
 .
.
или  . (7)
. (7)
Таким образом, если термодинамический процесс идеального газа действительно является политропным, т.е. молярная теплоёмкость в ходе процесса не изменяется, то её величина рассчитывается по формуле (7).
В настоящей работе используется модель одноатомного газа (i =3), поэтому в политропных процессах при n = -1 согласно выражению (7) молярная теплоёмкость С должна быть равна 16,6 Дж/моль×К, а при n = -2, C = 15,2 Дж/моль×К.
Частными случаями политропного процесса являются:
изотермический: n = 1, C = ± ¥;
изобарический: n = 0, C = Cp;
изохорический: n = ±¥, С = Сv;
4) адиабатический: n = g, где g =  , С = 0.
, С = 0.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

В прямоугольном окошке «Функция» нажмите маркером мыши кнопку «Прямая».
Подведите маркер мыши к выделенной левой точке графика р = f(V) на экране монитора, нажмите левую кнопку мыши, и, удерживая её в нажатом состоянии, переместите начало графика в точку с координатами (Р1,V1,Т1), взятыми из таблицы 1 для вашей бригады.
Аналогичным образом переместите выделенную крайнюю правую точку графика в точку с координатами (Р20, V20).
На мониторе щёлкните мышью кнопку;в верхнем ряду кнопок, а в
нижней части экрана кнопку «СТАРТ».


 Нажмите два раза кнопку 4 в верхнем ряду кнопок и запишите в первый столбец таблицы 2 значения
Нажмите два раза кнопку 4 в верхнем ряду кнопок и запишите в первый столбец таблицы 2 значения  Q и Т.
Q и Т.
Последовательно повторяя действия п.5 20 раз, заполните таблицу 2.
В прямоугольном окошке «Функция» нажмите маркером мыши кнопку «Парабола», проделайте измерения п.п. 2-6 и запишите результаты опытов в табл.3.
В прямоугольном окошке «Функция» нажмите маркером мыши кнопку «Экспонента», проделайте измерения п.п. 2-6 и запишите результаты опытов в табл.4.
ТАБЛИЦА 1. Начальные и конечные параметры для трёх термодинамических процессов
| Бригада
|
|
|
|
|
|
|
|
|
| Р1, кПа
|
|
|
|
|
|
|
|
|
| Р20, кПа
|
|
|
|
|
|
|
|
|
| V1, дм3
|
|
|
|
|
|
|
|
|
| V20, дм3
|
|
|
|
|
|
|
|
|
| Т1, К
|
|
|
|
|
|
|
|
|
ТАБЛИЦЫ 2,3,4. Результаты измерений температуры и количества выделения тепла в ходе термодинамического процесса расширения газа
Табл.2, функция «прямая»
Табл.3, функция «парабола»
Табл.4, функция «экспонента»
| № опыта (i)
|
|
|
|
|
|
|
|
|
|
|
| Ti
|
|
|
|
|
|
|
|
|
|
|
| Ti-T1
|
|
|
|
|
|
|
|
|
|
|
 Q Q
|
|
|
|
|
|
|
|
|
|
|
| № опыта (i)
|
|
|
|
|
|
|
|
|
|
|
| Ti
|
|
|
|
|
|
|
|
|
|
|
| Ti-T1
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА
1.Вычислите и запишите во вторую строку таблиц 2, 3, 4 разности температур Ti-T1.
3. На миллиметровой бумаге или на листе в клетку формата А4 постройте по экспериментальным точкам графики в виде линейной зависимости  от разности температур Ti-T1 для трёх исследуемых процессов. (Каждый график на отдельном листе!).
от разности температур Ti-T1 для трёх исследуемых процессов. (Каждый график на отдельном листе!).
4. По тангенсу угла наклона прямой линии графика к оси разности температур, используя формулу  , определите молярную теплоёмкость политропического процесса и сравните её с теоретическим значением, рассчитанным по формуле (7).
, определите молярную теплоёмкость политропического процесса и сравните её с теоретическим значением, рассчитанным по формуле (7).
5. Рссчитайте работу газа в этих процессах по формуле



и сравните эти значения со значениями, указанными в нижнем окне монитора при p20 и V20.
Проанализируйте полученные результаты, сделайте оценку погрешности измерений.
Вопросы и задания для самоконтроля
1. Сформулируйте закон Больцмана о равнораспределении энергии по степеням свободы молекул.
2. Почему колебательная степень свободы молекулы обладает вдвое большей энергией, чем поступательная и вращательная?
3. В чём состоит качественная неравноценность между работой и теплообменом как формами передачи энергии?
4. Что такое внутренняя энергия идеального газа?
5. В результате каких процессов может изменяться внутренняя энергия идеального газа?
6. Что называется молярной теплоёмкостью газа?
7. Почему Cv больше, чем CP?
8. Покажите применение первого начала термодинамики к изопроцессам в идеальных газах.
9. Чему равна работа изобарного расширения моля идеального газа при нагревании на 1К?
10. Чему равна работа изохорного расширения моля газа при нагревании на 1К?
11. Нагревается или охлаждается идеальный газ, если он расширяется при постоянном давлении?
12. Температура газа в сосуде постоянна. Запишите на основе первого начала термодинамики соотношение между сообщённым количеством теплоты и совершённой работой.
13. Газ переходит из одного и того же состояния u в одно и тоже состояние v в результате следующих процессов: 1) изотермического; 2) изобарного; 3) изохорного; 4) адиабатного. Рассмотрев эти процессы графически, показать: 1) в каком процессе работа расширения максимальна? 2) в каком случае газу сообщается большее количество тепла?
14. Какой процесс называется политропным?
15. Показатель политропы n >1. Нагревается или охлаждается идеальный газ при сжатии?
16. Определите, больше или меньше нуля молярная теплоёмкость газа в термодинамическом процессе  , если а) газ одноатомный; 2) газ двухатомный.
, если а) газ одноатомный; 2) газ двухатомный.






 ;
;  (1)
(1) =
=  ; (2)
; (2) . (3)
. (3) . (4)
. (4) =
=  . (5)
. (5) (6)
(6)


 (7) и
(7) и  (8) для каждого значения температуры рассчитайте среднюю арифметическую и среднюю квадратичную скорости газовых молекул и запишите эти величины в табл. 10.
(8) для каждого значения температуры рассчитайте среднюю арифметическую и среднюю квадратичную скорости газовых молекул и запишите эти величины в табл. 10. и
и  , по ним определите значение массы молекулы m0:
, по ним определите значение массы молекулы m0: (9)
(9)  (10)
(10)


 рассчитайте среднее значение импульса, передаваемого молекулами при соударении стенкам сосуда для каждого значения температуры. Значения m0 и
рассчитайте среднее значение импульса, передаваемого молекулами при соударении стенкам сосуда для каждого значения температуры. Значения m0 и  = f(T) и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
= f(T) и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
 и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
 и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа.
и проведите анализ соответствия качественного вида этого графика с выводами молекулярно- кинетической теории и с законами идеального газа. . (2)
. (2) , которую нужно сообщить одному молю вещества для изменения его температуры на 1К в рассматриваемом термодинамическом процессе:
, которую нужно сообщить одному молю вещества для изменения его температуры на 1К в рассматриваемом термодинамическом процессе: , (3) (M - молярная масса, m - масса газа).
, (3) (M - молярная масса, m - масса газа). . (4)
. (4) .
.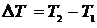 , то теплоёмкость газа постоянна и процесс является политропическим.
, то теплоёмкость газа постоянна и процесс является политропическим. .
. . (5)
. (5) . (6)
. (6) :
: .
. ,
, .
.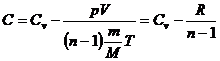 .
. , где
, где  показатель адиабаты, получим:
показатель адиабаты, получим: .
. . (7)
. (7) , С = 0.
, С = 0.

 Q и Т.
Q и Т. Q
Q


 от разности температур Ti-T1 для трёх исследуемых процессов. (Каждый график на отдельном листе!).
от разности температур Ti-T1 для трёх исследуемых процессов. (Каждый график на отдельном листе!). , определите молярную теплоёмкость политропического процесса и сравните её с теоретическим значением, рассчитанным по формуле (7).
, определите молярную теплоёмкость политропического процесса и сравните её с теоретическим значением, рассчитанным по формуле (7).
 , если а) газ одноатомный; 2) газ двухатомный.
, если а) газ одноатомный; 2) газ двухатомный.


