1). Постановка и особенности задачи.
2). Критерий Пирсона.
3). Понятие о критериях Колмогорова.
Постановка и особенности задачи.
Актуальной для практики задачей является аппроксимация (выравнивание) эмпирических распределений теоретическими, свойства которых известны. Другой важной задачей является сопоставление двух эмпирических распределений, полученных при различных условиях испытаний. Следовательно, принятие решений о законах распределения связано с двумя типами основных гипотез:
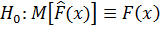
или 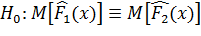
где 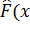 и F(x) – эмпирическое и теоретическое распределение соответсвенно.
и F(x) – эмпирическое и теоретическое распределение соответсвенно.
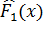 и
и 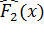 – эмпирические распределения, полученные при различных условиях испытаний.
– эмпирические распределения, полученные при различных условиях испытаний.
М – оператор математического ожидания.
В целом проверка этих гипотез проводится в полном соответствии с ранее рассмотренной схемой. Однако процедуре проверки присущи некоторые особенности.
Первая из них касается выбора класса распределений, относительно которых формируются гипотезы. Этот выбор осуществляется на основе анализа структуры объекта испытаний, характера опытных данных и свойств отдельных теоретических распределений. Из числа непрерывных распределений важную роль играют нормальное распределение, гамма-распределение, бета-распределение и другие.
Нормальное распределение отражает процессы, протекающие под воздействием большого числа факторов, среди которых нет явно доминирующих. Случайная величина при этом изменяется на бесконечном интервале, т.е. 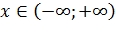 .
.
Гамма распределение является основным для неотрицательных случайных величин, когда 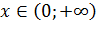 , характеризующих, например, промежутки времени между определенными событиями (в частности, отказами), когда поток этих событий является простейшим. Его частным случаем является экспоненциальное распределение.
, характеризующих, например, промежутки времени между определенными событиями (в частности, отказами), когда поток этих событий является простейшим. Его частным случаем является экспоненциальное распределение.
Бета-распределение основное для случайных величин, изменяющихся на интервале, когда 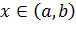 . Его частный случай – равномерное распределение.
. Его частный случай – равномерное распределение.
Следует помнить, что одной и той же основной гипотезе может удовлетворять несколько теоретических распределений. Принятие Н0 означает лишь то, что выбранное распределение не противоречит опытным данным. Продолжение испытаний может привести к опровержению сделанного заключения, причем для этого достаточно небольшого числа противоречащих Н0 результатов, в то время как для её подтверждения необходим большой объем испытаний. Тем самым реализуется принцип асимметрии решений.
Таким образом, выбор теоретических распределений не является формализованной процедурой и во многом определяется опытом исследователя.
Вторая особенность заключается в том, что критическая область всегда является правосторонней в силу специфики используемых критериев, сущность которой заключается в следующем.
Для того, чтобы принять или опровергнуть гипотезу Н0 , используют некоторую величину U, характеризующую расхождение между эмпирическим и теоретическим распределениями. Величина U может быть выбрана различными способами. Например, в качестве U можно взять модуль разности 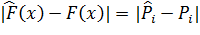 , где
, где
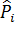 -эмпирическая вероятность на интервале (частоте),
-эмпирическая вероятность на интервале (частоте),
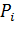 -теоретическая вероятность на том же интервале:
-теоретическая вероятность на том же интервале:
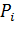 =
= 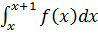
Лучше взять сумму квадратов этих разностей с некоторыми «весами», т.е. положить:
U = 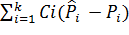 2
2
Где k – число интервалов или разрезов.
Коэффициенты 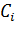 («веса» разрезов) вводятся потому что в общем случае отклонения, относящиеся к различным разрезам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение
(«веса» разрезов) вводятся потому что в общем случае отклонения, относящиеся к различным разрезам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение 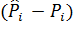 , может быть мало значительным, если сама вероятность
, может быть мало значительным, если сама вероятность 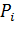 велика, и очень заметным, если мала.
велика, и очень заметным, если мала.
Допустим, что величина U выбрана тем или иным способом. Очевидно, что это есть случайная величина. Закон её распределения зависит от закона распределения Х и числа опытов n. Допустим, что это закон (для U) нам известен. В результате серии опытов получено, что выбранная нами мера расхождения приняла некоторое значение u. Спрашивается, можно ли объяснить это случайными причинами или же это расхождение слишком велико и указывает на наличие существенной разности между 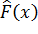 и
и 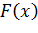 и, следовательно, на непригодность гипотезы Н0? Для ответа на это вопрос предположим, что Н0 верна, и вычислим в этом предположении вероятность того, что за счет случайных величин (n мало) мера U будет не меньше, чем наблюдаемое на опыте значение u, т.е.
и, следовательно, на непригодность гипотезы Н0? Для ответа на это вопрос предположим, что Н0 верна, и вычислим в этом предположении вероятность того, что за счет случайных величин (n мало) мера U будет не меньше, чем наблюдаемое на опыте значение u, т.е. 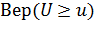 .
.
Если эта вероятность весьма мала, то гипотезу Н0 следует отклонить как мало правдоподобную. Если же эта вероятность значительна, то следует признать, что Н0 согласуется с опытом.
Очевидно, что 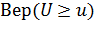 ≈ Вер(Ө>Ө2), что соответствует правосторонней критической области.
≈ Вер(Ө>Ө2), что соответствует правосторонней критической области.
При этом, поскольку проверка гипотез о законах распределения проводится всегда при сравнительно больших n, то уровень значимости критерия полагают равным
α =0,1; 0,2; 0,3; 0,4.
Критерий Пирсона
Применительно к гипотезе первого типа, т.е. к гипотезе
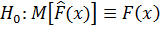
используются критерии Пирсона, Колмогорова и Мизеса-Крамера-Смирнова (критерий ω2).
Рассмотрим статистику критерия Пирсона или 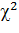 -критерия. Пусть произведено n независимых опытов, в каждом из которых случайная величина X принята определённое значение. Результаты опытов свезены в k разрядов и оформлены в виде статического ряда:
-критерия. Пусть произведено n независимых опытов, в каждом из которых случайная величина X принята определённое значение. Результаты опытов свезены в k разрядов и оформлены в виде статического ряда:
| Ji
| x1;x2
| x2;x3
| …………
| xi;xi+1
| …………
| xk;xk+1
|
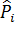
| 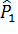
| 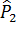
| …………
| 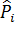
| …………
| 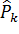
|

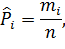
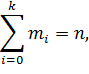
где Ji - i -тый интервал (разряд),
k -общее число интервалов,
mi - число значений в i -том разряде(число измерений величины X, попавших в i -й разряд).
Величина R=Хmax-Хmin называется размахом выборки.
Зная F(x), можно найти теоретические вероятности попадания величины X в каждый из разрядов:
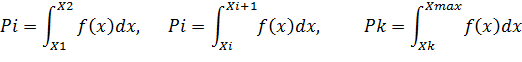
Пусть
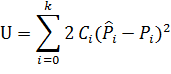
Если 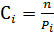 , то
, то
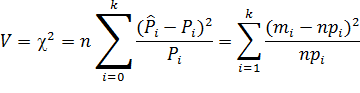
Это и есть статистика Пирсона.
Величина V имеет 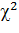 -распределение.
-распределение.
Распределением 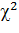 с ν степеней свободы называется распределение суммы квадратов ν независимых случайных величин, каждая из которых подчиняется нормальному закону с МОЖ=0 и
с ν степеней свободы называется распределение суммы квадратов ν независимых случайных величин, каждая из которых подчиняется нормальному закону с МОЖ=0 и 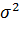 =1. Плотность его имеет вид:
=1. Плотность его имеет вид:
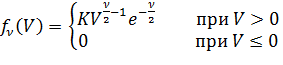
К= 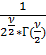 ;
;
Г(x)= 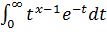 (гамма-функция или интеграл Эйлера 2-го рода).
(гамма-функция или интеграл Эйлера 2-го рода).
Критическое значение 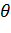 2=
2= 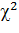 кр табулировано и находится по уровню значимости α и числу степеней свободы ν= k-l-1, где l -количество связей, определённые числом оценок параметров, вычисленных по данным выборки. Так для нормального распределения l =2, если оба параметра mx и
кр табулировано и находится по уровню значимости α и числу степеней свободы ν= k-l-1, где l -количество связей, определённые числом оценок параметров, вычисленных по данным выборки. Так для нормального распределения l =2, если оба параметра mx и 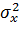 рассчитываются по результатам испытаний. В данной задаче число независимых случайных величин равно числу частот
рассчитываются по результатам испытаний. В данной задаче число независимых случайных величин равно числу частот 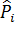 , то есть числу разрядов. Число независимых условий (связей), накладываемых на частоты
, то есть числу разрядов. Число независимых условий (связей), накладываемых на частоты 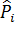 , равно 1, если мы требуем что бы
, равно 1, если мы требуем что бы 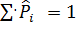 (это требование накладывается всегда). Число «связей» возрастает до двух, если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретические и статистическое средние, т.е.
(это требование накладывается всегда). Число «связей» возрастает до двух, если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретические и статистическое средние, т.е. 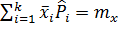 .
.
Наконец это число будет равно трём, если мы потребуем ещё совпадений теоретической и статистической дисперсии.
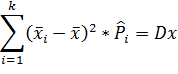
где 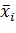 статистически среднее на i -том интервале.
статистически среднее на i -том интервале.
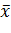 -общее статистическое среднее.
-общее статистическое среднее.
Гипотеза Н0 отклоняется если 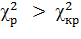
Критерий Пирсона используется при n ≥100 (хотя бы n ≥50)
Рекомендуемое число разрядов:
Длина интервала d=1,02 R/k
Для определения границ интервалов вычисляют:

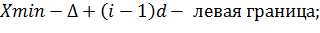

В интервал включаются и те наблюдения, которые приходятся на левую границу т.е. mi 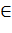 (di)
(di)
Понятие о критериях Колмогорова и Смирнова.
Кроме критерия Пирсона для оценки степени согласованности эмпирического и теоретического распределений на практике используется ряд других критериев, в частности, критерий Колмогорова. Статистика этого критерия имеет вид:
L 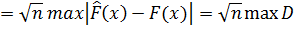
Как видно, в качестве меры расхождения принято наибольшее отклонение эмпирического распределения от теоретического, предсказываемого гипотезой. При неограниченном возрастании числа независимых испытаний n закон распределения статистически L имеет вид:
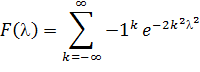
Функция распределения 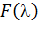 затабулирована (см.сборник таблиц Л.Н. Большева и Н.В. Смирнова- табл.6.1.Функция распределения Колмогорова). Задавшись уровнем значимости критерия a и памятуя о том, что критическая область является правосторонней, определяем по таблице критическое значение квантили:
затабулирована (см.сборник таблиц Л.Н. Большева и Н.В. Смирнова- табл.6.1.Функция распределения Колмогорова). Задавшись уровнем значимости критерия a и памятуя о том, что критическая область является правосторонней, определяем по таблице критическое значение квантили:
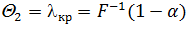
Если 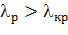 , то гипотеза Н0 отклоняется. Обычно
, то гипотеза Н0 отклоняется. Обычно 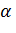 = 0,2….0,3. Критерий Колмогорова отличается простотой вычислений, но необходимо помнить о том, что он применим только для оценки непрерывных распределений при n >40…50 и только, когда теоретическое распределение не содержит неизвестных параметров. Такие случаи сравнительно редко встречаются на практике. Обычно из теоретических соображений известен только общий вид функции F(x), а входящие в неё параметры определяются по выборочным данным. При использовании критерия Пирсона это обстоятельство учитывается соответствующим уменьшении числа степеней свободы распределения
= 0,2….0,3. Критерий Колмогорова отличается простотой вычислений, но необходимо помнить о том, что он применим только для оценки непрерывных распределений при n >40…50 и только, когда теоретическое распределение не содержит неизвестных параметров. Такие случаи сравнительно редко встречаются на практике. Обычно из теоретических соображений известен только общий вид функции F(x), а входящие в неё параметры определяются по выборочным данным. При использовании критерия Пирсона это обстоятельство учитывается соответствующим уменьшении числа степеней свободы распределения 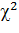 . Критерий Колмогорова такого согласования не предусматривает. Поэтому если его всё же применять в подобных случаях, то необходимо учитывать, что он будет давать заведомо завышенные значения
. Критерий Колмогорова такого согласования не предусматривает. Поэтому если его всё же применять в подобных случаях, то необходимо учитывать, что он будет давать заведомо завышенные значения 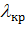 , в силу чего можно принять как правдоподобную гипотезу, в действительности плохо согласующуюся с опытными данными. Достоинством критерия Колмогорова является то, что при его использовании не требуется предварительного разбиения выборочных данных на интервалы.
, в силу чего можно принять как правдоподобную гипотезу, в действительности плохо согласующуюся с опытными данными. Достоинством критерия Колмогорова является то, что при его использовании не требуется предварительного разбиения выборочных данных на интервалы.
Наконец, критерий Колмогорова можно использовать и для проверки гипотез второго типа  , если объёмы выборок n1 и n2, соответствующие эмпирическим распределениям
, если объёмы выборок n1 и n2, соответствующие эмпирическим распределениям 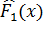 и
и 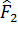 , достаточно велики. Статистика
, достаточно велики. Статистика 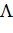 в этом случае имеет вид:
в этом случае имеет вид:
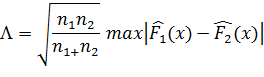
Для определения критической точки 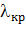 следует, как и прежде, воспользоваться табл.6.1 вышеуказанного сборника. Если же объёмы выборок невелики (n1 <20 и n2 <20), то для проверки однородности двух выборок используется критерий Смирнова и таблица 6.5а того же сборника.
следует, как и прежде, воспользоваться табл.6.1 вышеуказанного сборника. Если же объёмы выборок невелики (n1 <20 и n2 <20), то для проверки однородности двух выборок используется критерий Смирнова и таблица 6.5а того же сборника.



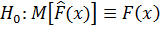
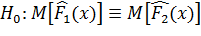
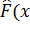 и F(x) – эмпирическое и теоретическое распределение соответсвенно.
и F(x) – эмпирическое и теоретическое распределение соответсвенно.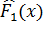 и
и 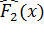 – эмпирические распределения, полученные при различных условиях испытаний.
– эмпирические распределения, полученные при различных условиях испытаний.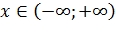 .
.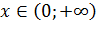 , характеризующих, например, промежутки времени между определенными событиями (в частности, отказами), когда поток этих событий является простейшим. Его частным случаем является экспоненциальное распределение.
, характеризующих, например, промежутки времени между определенными событиями (в частности, отказами), когда поток этих событий является простейшим. Его частным случаем является экспоненциальное распределение.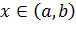 . Его частный случай – равномерное распределение.
. Его частный случай – равномерное распределение.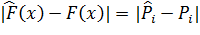 , где
, где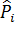 -эмпирическая вероятность на интервале (частоте),
-эмпирическая вероятность на интервале (частоте),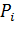 -теоретическая вероятность на том же интервале:
-теоретическая вероятность на том же интервале: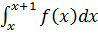
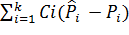 2
2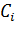 («веса» разрезов) вводятся потому что в общем случае отклонения, относящиеся к различным разрезам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение
(«веса» разрезов) вводятся потому что в общем случае отклонения, относящиеся к различным разрезам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение 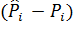 , может быть мало значительным, если сама вероятность
, может быть мало значительным, если сама вероятность 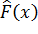 и
и 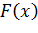 и, следовательно, на непригодность гипотезы Н0? Для ответа на это вопрос предположим, что Н0 верна, и вычислим в этом предположении вероятность того, что за счет случайных величин (n мало) мера U будет не меньше, чем наблюдаемое на опыте значение u, т.е.
и, следовательно, на непригодность гипотезы Н0? Для ответа на это вопрос предположим, что Н0 верна, и вычислим в этом предположении вероятность того, что за счет случайных величин (n мало) мера U будет не меньше, чем наблюдаемое на опыте значение u, т.е. 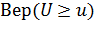 .
.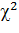 -критерия. Пусть произведено n независимых опытов, в каждом из которых случайная величина X принята определённое значение. Результаты опытов свезены в k разрядов и оформлены в виде статического ряда:
-критерия. Пусть произведено n независимых опытов, в каждом из которых случайная величина X принята определённое значение. Результаты опытов свезены в k разрядов и оформлены в виде статического ряда: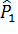
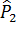
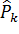

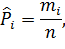
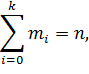
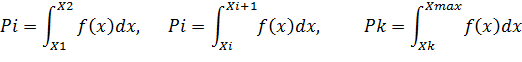
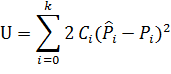
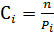 , то
, то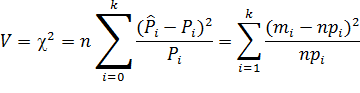
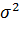 =1. Плотность его имеет вид:
=1. Плотность его имеет вид: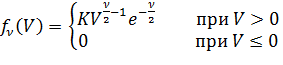
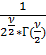 ;
;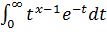 (гамма-функция или интеграл Эйлера 2-го рода).
(гамма-функция или интеграл Эйлера 2-го рода).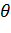 2=
2= 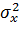 рассчитываются по результатам испытаний. В данной задаче число независимых случайных величин равно числу частот
рассчитываются по результатам испытаний. В данной задаче число независимых случайных величин равно числу частот 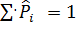 (это требование накладывается всегда). Число «связей» возрастает до двух, если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретические и статистическое средние, т.е.
(это требование накладывается всегда). Число «связей» возрастает до двух, если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретические и статистическое средние, т.е. 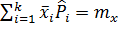 .
.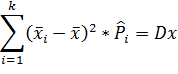
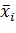 статистически среднее на i -том интервале.
статистически среднее на i -том интервале.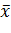 -общее статистическое среднее.
-общее статистическое среднее.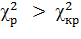

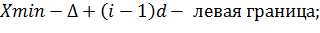

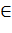 (di)
(di)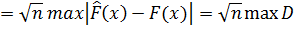
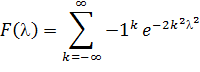
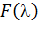 затабулирована (см.сборник таблиц Л.Н. Большева и Н.В. Смирнова- табл.6.1.Функция распределения Колмогорова). Задавшись уровнем значимости критерия a и памятуя о том, что критическая область является правосторонней, определяем по таблице критическое значение квантили:
затабулирована (см.сборник таблиц Л.Н. Большева и Н.В. Смирнова- табл.6.1.Функция распределения Колмогорова). Задавшись уровнем значимости критерия a и памятуя о том, что критическая область является правосторонней, определяем по таблице критическое значение квантили: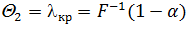
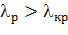 , то гипотеза Н0 отклоняется. Обычно
, то гипотеза Н0 отклоняется. Обычно 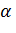 = 0,2….0,3. Критерий Колмогорова отличается простотой вычислений, но необходимо помнить о том, что он применим только для оценки непрерывных распределений при n >40…50 и только, когда теоретическое распределение не содержит неизвестных параметров. Такие случаи сравнительно редко встречаются на практике. Обычно из теоретических соображений известен только общий вид функции F(x), а входящие в неё параметры определяются по выборочным данным. При использовании критерия Пирсона это обстоятельство учитывается соответствующим уменьшении числа степеней свободы распределения
= 0,2….0,3. Критерий Колмогорова отличается простотой вычислений, но необходимо помнить о том, что он применим только для оценки непрерывных распределений при n >40…50 и только, когда теоретическое распределение не содержит неизвестных параметров. Такие случаи сравнительно редко встречаются на практике. Обычно из теоретических соображений известен только общий вид функции F(x), а входящие в неё параметры определяются по выборочным данным. При использовании критерия Пирсона это обстоятельство учитывается соответствующим уменьшении числа степеней свободы распределения 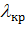 , в силу чего можно принять как правдоподобную гипотезу, в действительности плохо согласующуюся с опытными данными. Достоинством критерия Колмогорова является то, что при его использовании не требуется предварительного разбиения выборочных данных на интервалы.
, в силу чего можно принять как правдоподобную гипотезу, в действительности плохо согласующуюся с опытными данными. Достоинством критерия Колмогорова является то, что при его использовании не требуется предварительного разбиения выборочных данных на интервалы. , если объёмы выборок n1 и n2, соответствующие эмпирическим распределениям
, если объёмы выборок n1 и n2, соответствующие эмпирическим распределениям 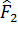 , достаточно велики. Статистика
, достаточно велики. Статистика 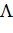 в этом случае имеет вид:
в этом случае имеет вид: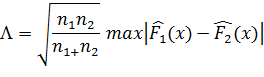
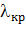 следует, как и прежде, воспользоваться табл.6.1 вышеуказанного сборника. Если же объёмы выборок невелики (n1 <20 и n2 <20), то для проверки однородности двух выборок используется критерий Смирнова и таблица 6.5а того же сборника.
следует, как и прежде, воспользоваться табл.6.1 вышеуказанного сборника. Если же объёмы выборок невелики (n1 <20 и n2 <20), то для проверки однородности двух выборок используется критерий Смирнова и таблица 6.5а того же сборника.


