Лекция 4. Статические гипотезы.
1). Основные определения и понятия.
2). Основные статистики.
3). Понятия о критической области.
4). Общая схема проверки статических гипотез.
Основные определения и понятия
В практике испытаний весьма распространенной является теория статических гипотез. Как и рассмотренные ранее принципы принятия статистических решений, эта теория призвана обеспечить анализ и оценку результатов испытаний с последующей формулировкой определенных выводов и решений.
Статической гипотезой называется любое предположительное суждение о вероятностных характеристиках одной или нескольких случайных величин.
Различают два вида статистических гипотез: о законах определения и о числовых характеристиках случайных величин (моментах, характеристиках положения).
Примеры статистических гипотез:
-случайная величина Х подчиняется нормальному закону распределения;
-математическое ожидание случайной величины Х равна а.
Гипотезы подлежат проверкt на основе результатов испытаний. Сущность проверки заключается в том, чтобы установить, согласуются ли опытные данные с выдвинутой гипотезой.
Дело в том, что на практике всегда будет иметь место расхождение между гипотезой и результатом выборочных наблюдений (число опытов всегда ограничено). Причинами такого расхождения могут быть либо случайные погрешности, обусловленные механизмом случайного отбора, либо систематически действующий фактор или факторы. Ответ на вопрос, какая из этих двух причин проявилась в ходе испытаний объекта, как раз и призвана дать теория проверки статистических гипотез. В зависимости от того, какой ответ будет получен, применяется то или иное статистическое решение, которое решающим образом предопределяет последующие за этим инженерные решения (например, доработать объект).
Гипотезы проверяются по определенным правилам. Эти правила называются статистическими критериями.
Критерии формируются на основе так называемых статистик.
Z- статистика
Двусторонняя КО
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
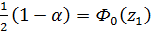 ;
;
 ;
;
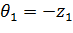 ;
;  .
.
 :
: 



 Но принимается
Но принимается
Односторонняя КО
 ;
;
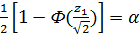 ;
;
 ;
;
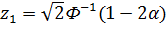 ;
;
 ;
;

 ;
;
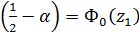 ;
;
 ;
;
 ;
;
 .
.
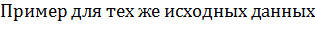 :
:
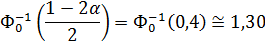

 Но отклоняется
Но отклоняется
Вывод: Односторонний критерий является более жестким.

OKO:  ;
;
ДКО:  ,
,  .
.
T- статистика

В силу четности f(x) табулируется не F(t), а функция 
Пример: 

Для ДКО:  ;
;  ;
;
Для ЛКО: 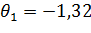 ;
;
Для ПКО:  ;
;
Т.к. 
Для сравнения:
 - интеграл ошибок (erf(z)) или функция Лапласа
- интеграл ошибок (erf(z)) или функция Лапласа
Ф(-z) = -Ф(z)
Ф 

F(z) = 
При альтернативе  критическая область будет двусторонней:
критическая область будет двусторонней:

Значение критических точек  определяется из уравнений:
определяется из уравнений:
 ;
;
 ;
;
 .
.

где  есть функции Лапласа
есть функции Лапласа
 ;
;

 .
.
При альтернативе  критическая область будет правосторонней и точка
критическая область будет правосторонней и точка  определится из уравнения:
определится из уравнения:
 ,
,
 .
.
Соответственно для  имеем левостороннюю область и
имеем левостороннюю область и

Пример 












| 
|
 Но принята Но принята
|  Но отклоняется Но отклоняется
|
Вывод: Односторонний критерий является более жестким, чем двусторонний.
Если дисперсия  известна, то используют статистику
известна, то используют статистику
 ,
,
где 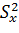 - статистическая дисперсия:
- статистическая дисперсия:


Известно:  , где v = n-1
, где v = n-1


Функция квавантилей для t –распределения рассчитана (затабулирована) на основе зависимости:
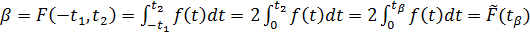 ,
,
где 
Поэтому:
 и
и

Пример



 v = 24
v = 24


 Но принимается
Но принимается
| 
 Но отклоняется
Но отклоняется
|
Сравнение средних двух совокупностей
Пусть имеются две выборки объемом  соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних
соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних  и
и  . Требуется проверить гипотезу
. Требуется проверить гипотезу  . Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
. Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
Первый вариант: дисперсии выборок  известны и равны друг другу, а так же
известны и равны друг другу, а так же  Рассмотрим разность
Рассмотрим разность 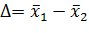 . Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза
. Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза 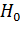 верна:
верна:
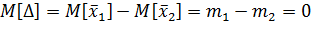

Выберем в качестве статистики величину
 ; D [
; D [ 
Если 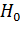 верна, то M [
верна, то M [ 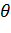 ], и D [
], и D [ 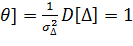 , т.е.
, т.е. 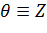 и поэтому дальнейшая проверка ведется по общей схеме.
и поэтому дальнейшая проверка ведется по общей схеме.
Второй вариант: выборки малы ( ),
),  неизвестны, то можно полагать (есть основания)
неизвестны, то можно полагать (есть основания)  .
.
Тогда определяют общую (двух выборок) статистическую дисперсию

где  – статистические дисперсии выборок.
– статистические дисперсии выборок.
На роль статистики принимают величину

которая подчиняется t - распределению с числом степеней свободы v=  .
.
Дальнейшая проверка ведется по общей схеме.
Третий вариант:  неизвестны и нет оснований полагать их равными, т.е.
неизвестны и нет оснований полагать их равными, т.е.  . Имеем проблему Беренса-Фишера.
. Имеем проблему Беренса-Фишера.
Пример
Вывод: Чем выше уровень доверительной вероятности, тем шире доверительный интервал!
Аналогичным образом можно определить доверительный интервал для дисперсии, если 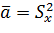 . Для этого достаточно воспользоваться V-статистикой, имеющей
. Для этого достаточно воспользоваться V-статистикой, имеющей 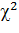 -распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
-распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
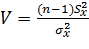 ,
,
откуда 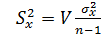
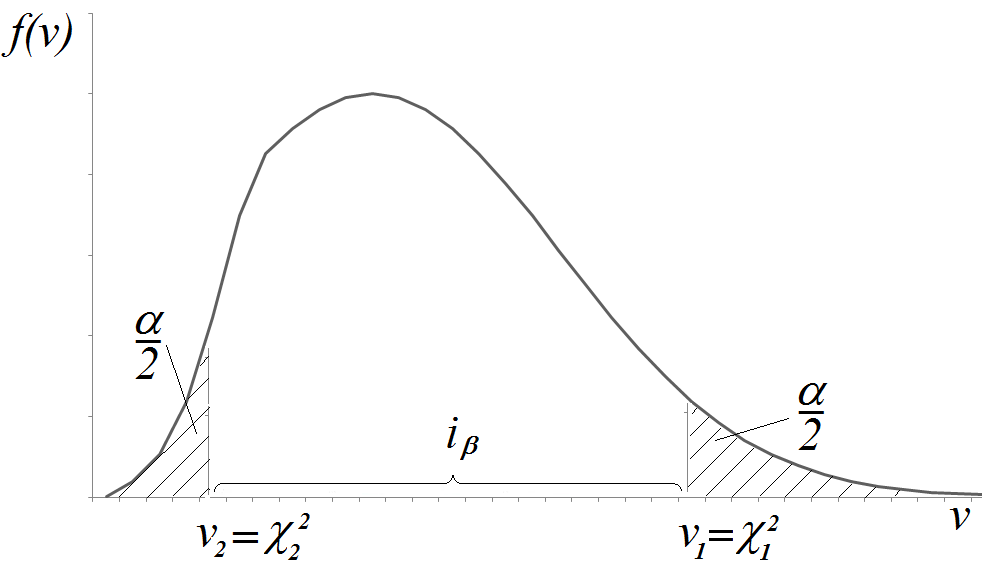
Как видно из рисунка, закон распределения статистики V в отличие от закона распределения статистики T не является симметричным. Поэтому возникает вопрос: как выбрать интервал 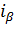 , в который величина V =
, в который величина V = 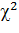 попадает с вероятностью
попадает с вероятностью 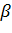 ?
?
Условимся выбирать интервал 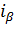 так, чтобы вероятности выхода величины V за пределы интервала вправо и влево (заштрихованные площади на рисунке) были одинаковы и равны
так, чтобы вероятности выхода величины V за пределы интервала вправо и влево (заштрихованные площади на рисунке) были одинаковы и равны
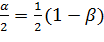 .
.
Чтобы построить интервал 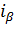 с таким свойством надо воспользоваться таблицей, в которой приведены числа
с таким свойством надо воспользоваться таблицей, в которой приведены числа 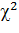 такие, что
такие, что
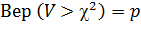 .
.
Зафиксировав ν = n-1, находят по таблице два значения 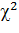 :
:
Одно 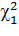 , отвечающие вероятности
, отвечающие вероятности 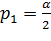 , и другое
, и другое 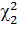 , отвечающее вероятности
, отвечающее вероятности 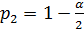 . Очевидно, что интервал
. Очевидно, что интервал 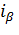 имеет
имеет 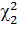 своим левым, а
своим левым, а 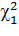 - правым концом.
- правым концом.
Теперь по интервалу 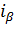 найдем искомый интервал
найдем искомый интервал 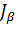 для неизвестной дисперсии
для неизвестной дисперсии 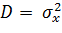 с границами
с границами 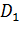 и
и 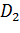 , который накрывает точку D с вероятностью
, который накрывает точку D с вероятностью 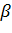 :
:
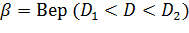
Для этого убедимся в равносильности неравенств:
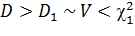
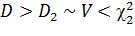 ,
,
Откуда:
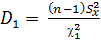 и
и 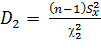
Пример:
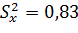
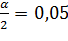
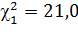
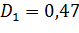
n =13 ν = 12 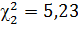
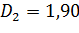
Если интегрировать слева направо:
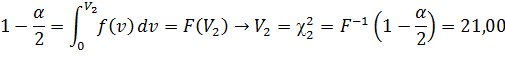
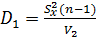
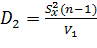
Лекция 10. Исходные понятия теории статистического анализа
1). Предмет и общая задача статистического анализа.
2). Формы взаимосвязи между переменными в задачах СА. Сущность понятия стохастической зависимости.
3). Частные задачи, виды и основные этапы статистического анализа.
Предмет и общая задача статистического анализа.
Определение вероятностных характеристик случайных величин и процессов по опытным данным и формирование на этой основе соответствующих выводов- предмет теории статистических решений.
Установление причинно-следственных механизмов взаимосвязи между случайными величинами, определяющими состояние и развитие испытываемого объекта или изучаемого явления- предмет статистического анализа (СА).
Задачи СА подразделяются на общую и частные. Рассмотрим суть общей задачи. Ее формулировка предполагает рассмотрение объекта испытаний совместно с характеризующими его переменными величинами. Последние подразделяются на входные и выходные (результирующие). Входные переменные представляют собой характеристики воздействующих на объекты факторов. Поэтому для краткости они именуются просто факторами и обозначаются через Х. Различают управляемые и латентные факторы. Первые представляют собой контролируемые исследователем характеристики, уровни которых он может задавать (фиксировать) с требуемой точностью. Латентные это скрытые, не поддающиеся учету и измерению факторы, в том числе ошибки измерения управляемых факторов. В математических моделях их для краткости именуют остатками и обозначают через Е.
Выходные переменные представляют собой результат преобразования объектом входных переменных, в следствии чего они называются откликами. Отклики принято обозначать через Y.
В общем случае факторы Х и отклики Y суть многокомпонентные случайные векторы, образующие систему (Х, У):
 (10.1)
(10.1)
Система (10.1) полностью характеризует объект с точки зрения типовых задач статистического анализа.
По результатам испытаний объекта формируется выборка объемом n, представляющая собой совокупность n опытных значений системы (10.1):
 (10.2)
(10.2)
Общая задача СА заключается в том, чтобы на основе опытных данных, представленных выборкой (10.2), сформировать некий оператор A(X,E), связывающий вектор Y с вектором Х и позволяющий наилучшим, в определенном смысле, образом прогнозировать отклик объекта на заданные воздействия (факторы), т.е. получить:
Y=A(X, E) (10.3)
Выражение (10.3) следует рассматривать не как строгое математическое соотношение, а как чисто формальную запись (знаковое представление) тезиса о наличии связи между откликом и факторами. Вопрос о том, в какой форме может проявиться эта связь, рассмотрим ниже. В случае ее конкретизации выражение (10.3) превращается в математическую модель объекта. Поэтому общая задача СА есть не что иное, как задача идентификации объекта по результатам испытаний.
Формы взаимосвязи между переменными в задачах СА. Сущность понятия стохастической зависимости.
В общем случае связь между откликами и факторами может проявиться в одной из форм, представленных в табл. 10.1.
Из табл. 10.1 видно, что результат (отклик) всегда случаен. Но причины этой случайности различны для различных форм зависимости.
Таблица 10.1.
Формы связи между откликом и факторами
| Отклик
| Факторы
| Зависимость
| Форма записи
| Предмет теории…
|
| Y
| x
| Функциональная
| Y=ϕ(x)+E
| Статистических решений
|
| Y
| X
| функциональная
| Y=ϕ(Х)
| Статистических решений
|
| Y
| x
| Стохастическая
| Y=  (x) (x)
| Регрессионного анализа
|
| y
| X
| Полная стохастическая
| Y=  (Х) (Х)
| Корреляционного анализа
|
Обозначения принятые в табл. 10.1:
х - неслучайный вектор факторов,
Х - случайный вектор факторов,
ϕ(x) - неслучайная функция неслучайных аргументов,
 (x) - условное обозначение стохастической зависимости между Х и Y,
(x) - условное обозначение стохастической зависимости между Х и Y,
 (Х) - условное обозначение полной стохастической зависимости между Х и Y.
(Х) - условное обозначение полной стохастической зависимости между Х и Y.
В случаях функциональной зависимости такими причинами являются либо латентные факторы, либо случайный характер факторов. Оценка результатов испытаний в этих случаях базируется на положениях теории статистических решений и выливается в конечном итоге либо в одно из решений на множестве D, либо в принятие (отклонение) статистической гипотезы, либо в точечную или интервальную оценку исследуемого параметра объекта. В любом из этих случаев нет надобности строить математическую модель объекта, т.к. вид функции ϕ известен заранее. Если же это не так (задачи прогностики), то вид функции ϕ постулируется, а входящие в нее параметры определяются на основе опытных данных методом наименьших квадратов (МНК).
Что же касается случаев стохастической зависимости, то они предполагают построение моделей типа ϕ(x) в качестве самостоятельной задачи оценки результатов испытаний. В связи с этим остановимся подробнее на понятии стохастической зависимости.
Понятие зависимость между компонентами системы случайных величин (X, Y) удобно установить по аналогии с понятием зависимости между событиями А и В, если под событием А понимать выполнение неравенства Х<x, а под событием В- выполнение неравенства Y<y. Тогда величины X и Y независимы, если вероятность совместного наступления этих двух событий для любых x и y равна произведению вероятностей проявления каждого из них, т.е.
P(AB)=P((Х<x)(Y<y))= P(Х<x)P(Y<y)=P(A)P(B)
Заменив вероятности функциями распределения, получим определение независимости в виде равенства:
F(x,y)=F(x)F(y) (10.4)
Если функцию распределения F(x,y) невозможно представить в виде (10.4), то величины X и Y зависимы.
Для непрерывных случайных величин условие (10.4) можно выразить через дифференциальную функцию распределения:
f(x,y)=f(x)f(y) (10.5)
Условия зависимости между X и Y выражается через плотности условных распределений f(y/x) или f(x/y), под которыми подразумевают плотность одной случайной величины при конкретном значении другой, т.е. f(y/x) представляет функцию плотности распределения величины Y, полученную при условии, что случайная величина Х приняла значение х.
Для зависимых случайных величин справедливо соотношение:
f(x,y) =  , (10.6)
, (10.6)
где  и
и  (10.7)
(10.7)
Зависимости (10.7) определяют плотности так называемых маргинальных (предельных) распределений. Используя их можно найти плотности условных распределений:
 (10.8)
(10.8)
Корреляционным анализом называется совокупность методов статистической обработки результатов испытаний, зависящих от различных одновременно действующих факторов, с целью анализа и оценки существенности влияния данных факторов на отклик.
В отличие от дисперсионного анализа, при проведении которого любые факторы рассматриваются как качественные, в корреляционном анализе могут рассматриваться как качественные, так и количественные факторы, хотя предпочтение отдается последним.
Сущность корреляционного анализа заключается в установлении стохастической зависимости между откликом и факторами и в определении существенности влияния факторов на отклик, степени тесноты стохастической связи между ними. Смысл понятия «корреляционная зависимость» удобнее рассматривать для случая одномерных фактора и отклика, образующих систему случайных величин (X,Y).
Прежде всего, необходимо отметить, что корреляционная зависимость является разновидностью стохастической зависимости и уже по этой причине не является жесткой, функциональной. При изучении такой зависимости между компонентами системы (X,Y) возможны 2 различных подхода к формированию исходных предположений. Первый заключается в том, что определяемые значения переменной X задаются, т.е. не являются случайными. Тогда каждому фиксированному значению х соответствуют некоторые генеральные распределения Y/х с математическим ожиданием M[Y/x] и дисперсией D[Y/x], а наблюдаемые на опыте значения у рассматриваются как выборочные значения из этой генеральной совокупности. Зависимость M[Y/x] = φу(х) называется, как уже отмечалось, регрессией Y на Х.
Второй подход к формированию исходных предположений состоит в том, что реализации случайной переменной Х, т.е. значения х, не задаются, а генерируются датчиком нормально распределенных чисел. А так как одно из основных допущений корреляционного анализа, как и дисперсионного, заключается в предположении о том, что участвующие в анализе переменные распределены нормально, это следует признать, что в этом случае реализации Х и Y, наблюдаемые на опыте, будут представлять собою выборку из двумерного нормального распределения. При таком варианте исходных предположений компоненты системы (X,Y) становятся как бы полностью «равноправными». Вследствие чего необходимо вести речь о регрессии Y на Х, но и о регрессии Х на Y, т.е. о зависимости:
M [Х/у] = φх(у)
Поэтому приходим к выводу, что корреляционная зависимость, как разновидность стохастической, может быть представлена двумя уравнениями регрессии - φу(х) и φх(у).
Зависимости φу(х) и φх(у) могут быть как линейными, так и не линейными. Соответственно различают линейный и нелинейный корреляционный анализ. Обычно предполагается линейный характер этих регрессий. В этом предположении заключается второе из основных допущений корреляционного анализа (первое предполагает нормальность распределения компонент Х и Y). Оно гласит: регрессия имеет линейный или близкий к линейному характер.
Поэтому обычно полагают:
φу(х) = β0 + βх (12.1)
φх(у) = γ0 + γy
Такая связь или корреляция называется парной. Если с увеличением одной из компонент условное среднее другой также возрастает, то корреляция называется положительной, в противном случае – отрицательной.
Для определения коэффициентов в уравнениях (12.1) используются диаграммы или корреляционные поля. Каждая точка такого поля имеет координаты xi, yi , соответствующие значениям переменных в i -том опыте. Обработка опытных данных ведется методом наименьших квадратов. В итоге получают оценку b0 для β0, b для β и т.д.
Эта процедура называется параметризацией уравнений (12.1).
Определение характера зависимостей φу(х) и φх(у), т.е. установление формы стохастической связи между компонентами Х и Y, является одной из основных задач корреляционного анализа. Вторая основная задача заключается в определении существенности этой связи, т.е. существенности взаимовлияния компонент Х и Y. С решением этих задач связанны основные процедуры корреляционного анализа, рассмотренные в следующем параграфе.
В заключение отметим основные виды корреляционного анализа. Они различаются:
-по количеству факторов – однофакторный, многофакторный (множественный);
-по количеству откликов – одномерный, многомерный (векторный);
-по форме стохастической связи – линейный, нелинейный.
Однофакторный корреляционный анализ.
Основные этапы и соответствующие им процедуры корреляционного анализа рассмотрим на примере однофакторного одномерного анализа, позволяющего изучить взаимовлияние двух случайных компонент – фактора Х и отклика Y.
Первым этапом корреляционного анализа является установление наличия стохастической связи между компонентами Х и Y. Для этого используются рассмотренные ранее процедуры дисперсионного анализа. Если по итогам дисперсионного анализа делается вывод о наличии стохастической связи, то переходят ко второму этапу.
Вторым этапом является установление формы стохастической связи, т.е. решение вопроса о том, линейна она или нелинейна. Решение данной задачи может проводиться качественными и количественными методами.
Качественные методы опираются на анализ поля корреляции, а количественные – на методы построения кривой, наилучшим образом аппроксимирующей результаты наблюдений. В случае использования количественных методов выдвигается гипотеза о типе кривой, а затем осуществляется её параметризация, например, с помощью метода наименьших квадратов. В полном объеме эта процедура рассматривается на заключительных этапах регрессионного анализа.
Третьим, заключительным этапом корреляционного анализа является определение существенности стохастической связи между фактором и откликом.
Если стохастическая связь между переменными является линейной, то мерой этой связи служит парный коэффициент корреляции, определяемый выражением:
rхy =Кху/ϬхϬу =М[(X-mх)(Y-mу)] /ϬхϬу (12.2)
Если исследуемые переменные связаны функциональной зависимостью, то rхy=±1, а в случае их независимости rхy=0.
На практике используется оценка парного коэффициента корреляции, определяемая по опытным данным:
 (12.3)
(12.3)
Значимость этой оценки проверяется на основе гипотез:
H0: rхy = 0
H1: rхy ≠ 0
В случае большой выборки оценка  распределена по нормальному закону с параметрами:
распределена по нормальному закону с параметрами:
M [  ] = 0
] = 0
D [  ] = (1- rхy2)2 /n
] = (1- rхy2)2 /n
Поэтому основная гипотеза может быть проверена с использованием Z – статистики, при формировании которой следует использовать оценку дисперсии D [  ], т.е.
], т.е. 
Если выборка не является большой, то используется статистика
 , (12.4)
, (12.4)
которая подчиняется t – распределению с числом степеней свободы υ = n-2.
В случае отклонения основной гипотезы выборочный коэффициент корреляции признается значимым с выбранным уровнем значимости. Он характеризует степень приближения стохастической зависимости между переменными к линейной. Для количественной оценки нелинейности используется так называемый коэффициент детерминации ɳху, который определяется как rхy2. Этот коэффициент позволяет ответить на вопрос о том, каково качество описания зависимости с помощью уравнения регрессии. Очевидно, чем теснее наблюдения примыкают к линии регрессии, тем лучше она описывает соответствующую зависимость переменных и с большей надежностью может быть применена для оценивания значений отклика по заданным значениям фактора.
Можно показать, что rхy2 равен отношению межуровневой дисперсии к общей дисперсии отклика, откуда следует, что коэффициент детерминации характеризует долю так называемой объясненной регрессией дисперсии в общей величине дисперсии. Чем теснее наблюдения примыкают к линии регрессии, тем эта доля выше. Например, если rхy =0,9, то ɳху = rхy2 = 0,81. Это значит, что 81% общей дисперсии (общей для среднего значения отклика) определяется уравнением регрессии, т.е. корреляционная связь между откликом и фактором вполне удовлетворительно может быть представлена линейным уравнением, т.к. доля нелинейности сравнительно невелика.
Проверкой значимости оценки rхy завершаются основные процедуры корреляционного анализа.
Чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора определяется знаками этого столбца.
Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной ПФЭ 23
Эксперимент, в котором реализуется определенная часть всех возможных сочетаний уровней факторов, называется дробным факторным экспериментом (ДФЭ), а соответствующая матрица спектра – дробной репликой. Если реализуется половина всех возможных сочетаний уровней, то матрица называется полурепликой, если четвертая часть – четвертьрепликой и т.д. В общем случае можно рассматривать реплики большей дробности.
Для обозначения дробных реплик, в которых Р линейных эффектов приравненых к эффектам взаимодействия, используется обозначения 2к-р. Например, полуреплика от плана ПФЭ 23 обозначается 23-1, а четвертьреплика ПФЭ 25 – 25-2.
Выбор полуреплик. Генерирующие соотношения и определяющие контрасты.
При построении полуреплики 23-1 существуют всего две возможности: приравнять x3 к “ +x1x2 ” или к “ -x1x2 ”, как показано в таблице:
Полуреплики 23-1
| Номер опыта
| I) x3=+x1x2
| Номер опыта
| II) x3=-x1x2
|
|
| X1
| X2
| X3
| X1X2X3
| X1
| X2
| X3
| X1X2X3
|
|
|
| +
| +
| +
| +
|
| +
| +
| -
| -
|
|
| -
| -
| +
| +
|
| -
| -
| -
| -
|
|
| +
| -
| -
| +
|
| +
| -
| +
| -
|
|
| -
| +
| -
| +
|
| -
| +
| +
| -
|
| | | | | | | | | | | |
Обе полуреплики равнозначны. Обратим внимание, что для произведения трех столбцов матрицы I выполняется соотношение +1= x1x2x3, а для матрицы II имеем -1= x1x2x3
Символическое обозначение произведения столбцов, равного +1 или -1, называется определяющим контрастом.
Определяющий контраст используется для определения системы смешивания оценок. Для того, чтобы определить какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту. Так, для матрицы I система смешивания будет иметь вид
Для x1  x1=x12x2x3 = x2x3, b1 → β1 + β23
x1=x12x2x3 = x2x3, b1 → β1 + β23
Для x2  x2=x1x22 x3 = x1x3, b2 → β2 + β13
x2=x1x22 x3 = x1x3, b2 → β2 + β13
Для x3  x3=x1x2x32 = x1x2, b3 → β3 + β12
x3=x1x2x32 = x1x2, b3 → β3 + β12
В случае использования матрицы II получим:
b1 → β1 - β23 b2 → β2 - β13 b3 → β3 – β12
Соотношение, показывающее, с каким из эффектов смешан данный эффект, называется генерирующим соотношением.
24-1
23
X4
X1 x2 x3 x1x2 x1x3 x2x3 x1x2 x3 x1x2 x3 x1x2 x4
1 - - - + + + - - +
2 + - - - - + + - +
3 - + - - + - + - +
4 + + - + - - - - +
5 - - + + - - + + +
6 + - + + - + - + +
7 - + + - - + - + +
8 + + + + + + + + +
+1= x1x2x4
+1= x1x3x4
+1= x2x3x4
+1= x1x2x3x4
-1= x1x2x4
-1= x1x3x4
-1= x2x3x4
-1= x1x2x3x4
В данном случае возможны варианты:
1) x4=x1x2
2) x4=x1x3
3) x4=x2x3
4) x4=x1x2x3
5) x4= -x1x2
6) x4= -x1x3
7) x4= -x2x3
8) x4= -x1x2x3
Остановимся на 1 и 4 вариа



 ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
;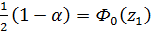 ;
; ;
;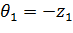 ;
;  .
. :
: 



 Но принимается
Но принимается ;
;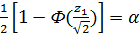 ;
; ;
;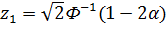 ;
; ;
;
 ;
;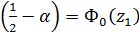 ;
; ;
; ;
; .
.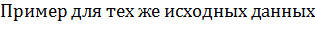 :
: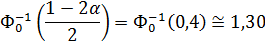

 Но отклоняется
Но отклоняется
 ;
; ,
,  .
.



 ;
;  ;
;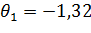 ;
; ;
;
 - интеграл ошибок (erf(z)) или функция Лапласа
- интеграл ошибок (erf(z)) или функция Лапласа


 критическая область будет двусторонней:
критическая область будет двусторонней:
 определяется из уравнений:
определяется из уравнений: ;
; ;
; .
.
 есть функции Лапласа
есть функции Лапласа ;
;
 .
. критическая область будет правосторонней и точка
критическая область будет правосторонней и точка  определится из уравнения:
определится из уравнения: ,
, .
. имеем левостороннюю область и
имеем левостороннюю область и












 известна, то используют статистику
известна, то используют статистику ,
,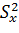 - статистическая дисперсия:
- статистическая дисперсия:

 , где v = n-1
, где v = n-1

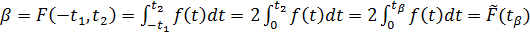 ,
,
 и
и


 Но принимается
Но принимается
 Но отклоняется
Но отклоняется
 соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних
соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних  и
и  . Требуется проверить гипотезу
. Требуется проверить гипотезу  . Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
. Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты. известны и равны друг другу, а так же
известны и равны друг другу, а так же  Рассмотрим разность
Рассмотрим разность 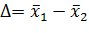 . Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза
. Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза 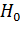 верна:
верна: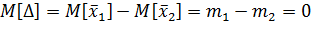

 ; D [
; D [ 
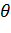 ], и D [
], и D [ 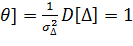 , т.е.
, т.е. 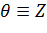 и поэтому дальнейшая проверка ведется по общей схеме.
и поэтому дальнейшая проверка ведется по общей схеме. ),
),  неизвестны, то можно полагать (есть основания)
неизвестны, то можно полагать (есть основания)  .
.
 – статистические дисперсии выборок.
– статистические дисперсии выборок.
 .
. . Имеем проблему Беренса-Фишера.
. Имеем проблему Беренса-Фишера.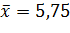 ;
;
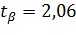
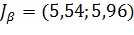
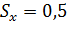 ;
;
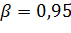
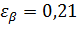
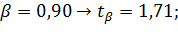
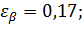
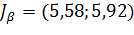
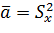 . Для этого достаточно воспользоваться V-статистикой, имеющей
. Для этого достаточно воспользоваться V-статистикой, имеющей 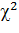 -распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
-распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид: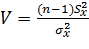 ,
,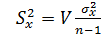

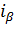 , в который величина V =
, в который величина V = 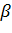 ?
?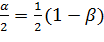 .
.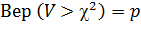 .
.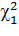 , отвечающие вероятности
, отвечающие вероятности 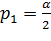 , и другое
, и другое 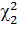 , отвечающее вероятности
, отвечающее вероятности 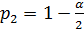 . Очевидно, что интервал
. Очевидно, что интервал 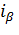 имеет
имеет 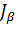 для неизвестной дисперсии
для неизвестной дисперсии 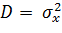 с границами
с границами 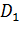 и
и 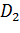 , который накрывает точку D с вероятностью
, который накрывает точку D с вероятностью 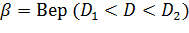
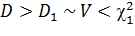
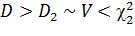 ,
,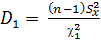 и
и 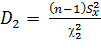
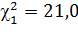
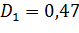
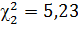
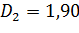
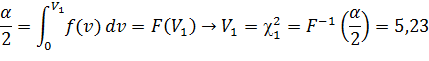
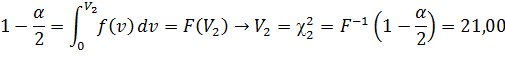
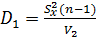
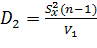
 (10.1)
(10.1) (10.2)
(10.2) (x)
(x)
 (x) - условное обозначение стохастической зависимости между Х и Y,
(x) - условное обозначение стохастической зависимости между Х и Y, , (10.6)
, (10.6) и
и  (10.7)
(10.7) (10.8)
(10.8) (12.3)
(12.3) распределена по нормальному закону с параметрами:
распределена по нормальному закону с параметрами:
 , (12.4)
, (12.4) x1=x12x2x3 = x2x3, b1 → β1 + β23
x1=x12x2x3 = x2x3, b1 → β1 + β23


