ДИФРАКЦИОННОЙ РЕШЕТКИ
Цель работы: определение периода, числа штрихов на один миллиметр, угловой дисперсии и разрешающей способности дифракционной решетки.
Теоретические положения
Дифракционная решетка – оптический прибор, представляющий собой совокупность большого числа параллельных, равноотстоящих друг от друга узких щелей (штрихов) одинаковой формы, нанесенных на какую-либо поверхность. Основное свойство дифракционной решетки – способность раскладывать падающий на нее свет в спектр по длинам волн. Различают отражательные и прозрачные дифракционные решетки. У отражательных штрихи наносятся на зеркальную (как правило, металлическую) поверхность, наблюдение спектра ведется в отраженном свете.
 У прозрачных решеток штрихи наносятся на поверхность прозрачной (как правило, стеклянной) пластины либо вырезаются в виде узких щелей в непрозрачном экране и наблюдение ведется в проходящем свете.
У прозрачных решеток штрихи наносятся на поверхность прозрачной (как правило, стеклянной) пластины либо вырезаются в виде узких щелей в непрозрачном экране и наблюдение ведется в проходящем свете.
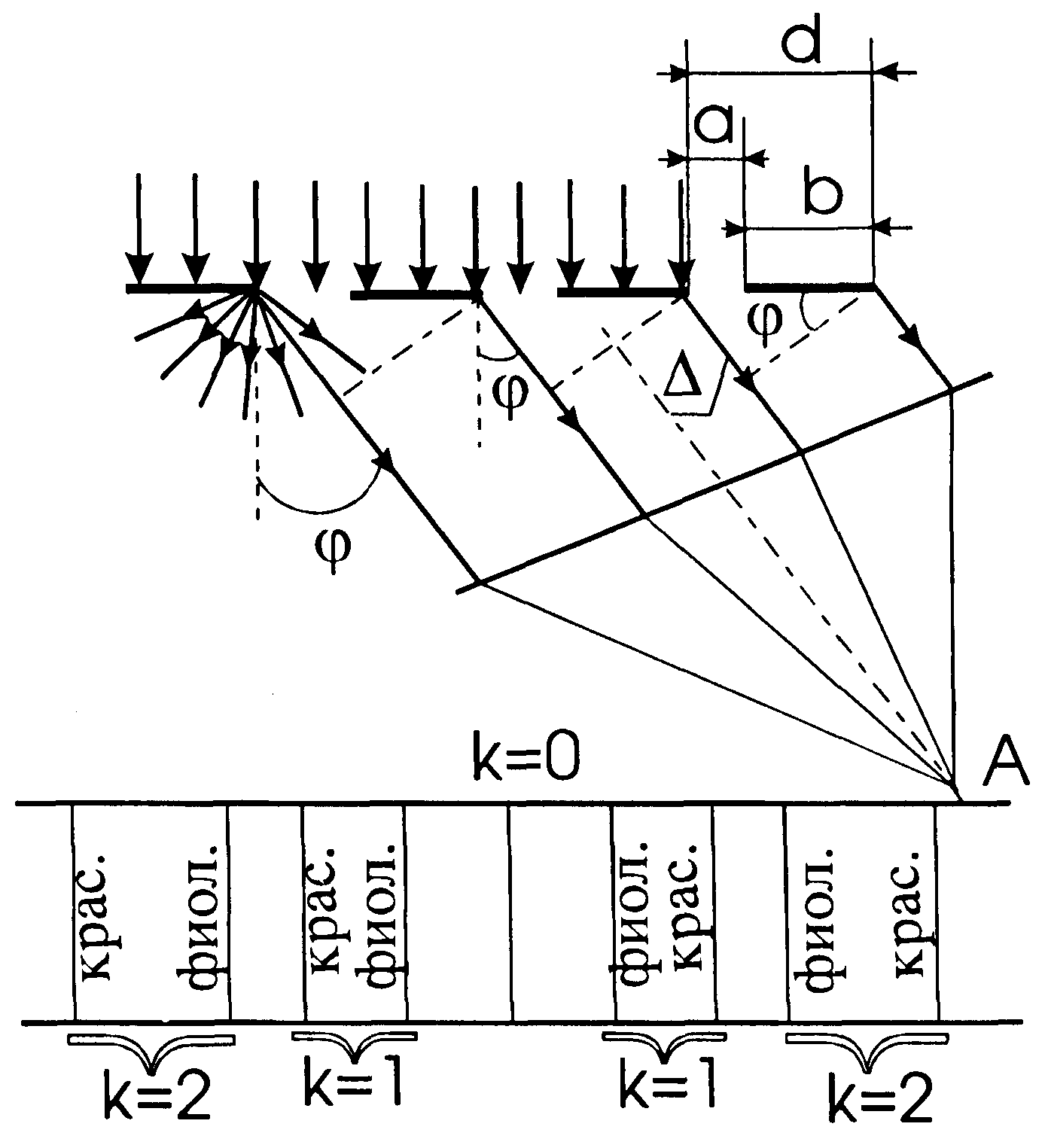
Рассмотрим действие прозрачной дифракционной решетки. Пусть на решетку нормально к ее поверхности падет параллельный пучок белого света (рис. 3.28.1). На щелях (штрихах) решетки, соизмеримых с длиной волны света, происходит явление дифракции, определенное как отклонение волн от прямолинейного распространения при взаимодействии их с препятствием. В результате за решеткой лучи пойдут под разными углами во все стороны от каждой точки щели. Эти лучи можно сгруппировать в пучки параллельных между собой лучей. Установим за решеткой положительную линзу. Каждый пучок параллельных лучей соберется в задней фокальной плоскости линзы в одной точке (точка А для лучей, дифрагировавших под углом
φ к нормали решетки). Параллельные лучи других углов дифракции линза собирает в других точках фокальной плоскости. В этих точках произойдет интерференция световых волн, исходящих от разных щелей решетки. Если в разности хода между соответствующими лучами укладывается целое число длин волн монохроматического света, то в точке встречи лучей возникает максимум интенсивности света для данной длины волны, то есть Δ =
k λ,
k = 0, ±1, ±2,....
Из рис. 3.28.1 видно, что разность хода Δ между двумя параллельными лучами, выходящими из соответствующих точек соседних щелей, равна
Δ = (а + b). sin φ = d · sin φ, (3.28.1)
где а – ширина щели; b – ширина непрозрачного промежутка между щелями.
Величина d = а + b называется периодом, или постоянной дифракционной решетки. Следовательно, условие возникновения главных интерференционных максимумов решетки имеет вид
d sinφ = Δ = k λ. (3.28.2)
В фокальной плоскости линзы для лучей, не испытавших дифракции, наблюдается центральный белый максимум нулевого порядка (φ = 0, k = 0), вправо и влево от которого симметрично располагаются цветные максимумы (спектральные линии) первого, второго и последующих порядков интерференции (см. рис. 3.28.1). Интенсивность максимумов сильно уменьшается с ростом их порядка, то есть с увеличением угла дифракции.
Уравнение (3.28.2) позволяет рассчитать период дифракционной решетки d, если измерен угол дифракции φ, соответствующий спектральной линии, для которой известны ее длина волны и порядок спектра.
Зная период решетки, легко рассчитать число штрихов, нанесенных на один миллиметр ширины решетки:
 , (3.28.3)
, (3.28.3)
где l – ширина решетки.
Одной из основных характеристик дифракционной решетки является ее угловая дисперсия. Угловой дисперсией решетки D называется величина, определяемая приращением угла дифракции при изменении длины волны на единицу, то есть
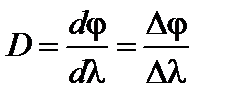 . (3.28.4)
. (3.28.4)
Дисперсия определяет угловое расстояние dφ между направлениями двух спектральных линий, отличающихся по длине волны на 1 нм (d λ = 1нм), и характеризует степень растянутости спектра вблизи данной длины волны. Формула для расчета угловой дисперсии решетки может быть получена при дифференцировании уравнения, определяющего положение главных максимумов d sin φ = k λ, откуда
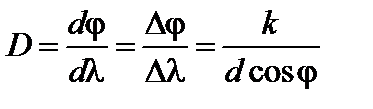 . (3.28.5)
. (3.28.5)
Из этого выражения следует, что угловая дисперсия решетки тем больше, чем больше порядок спектра. Этим объясняется расширение спектра одного порядка у решеток с ростом порядка.
Для решеток с разными периодами ширина спектра больше у решетки с меньшим периодом. Обычно в пределах одного порядка cos φ меняется незначительно (особенно для решеток с небольшим числом штрихов на миллиметр), поэтому дисперсия в пределах одного порядка почти не меняется. Спектр, полученный при постоянной дисперсии, растянут равномерно во всей области длин волн, что выгодно отличает спектр решетки от спектра, даваемого призмой.
В спектроскопии принято считать, что оптический прибор разрешил две линии спектра, если изображения этих линий в спектре, полученном с помощью данного прибора, видны раздельно. Если изображения двух линий сливаются в одну, то говорят, что прибор их не разрешил. Одни и те же линии спектра могут быть разрешены одним прибором и не разрешены другим. Это связано с шириной максимумов интенсивности этих линий.
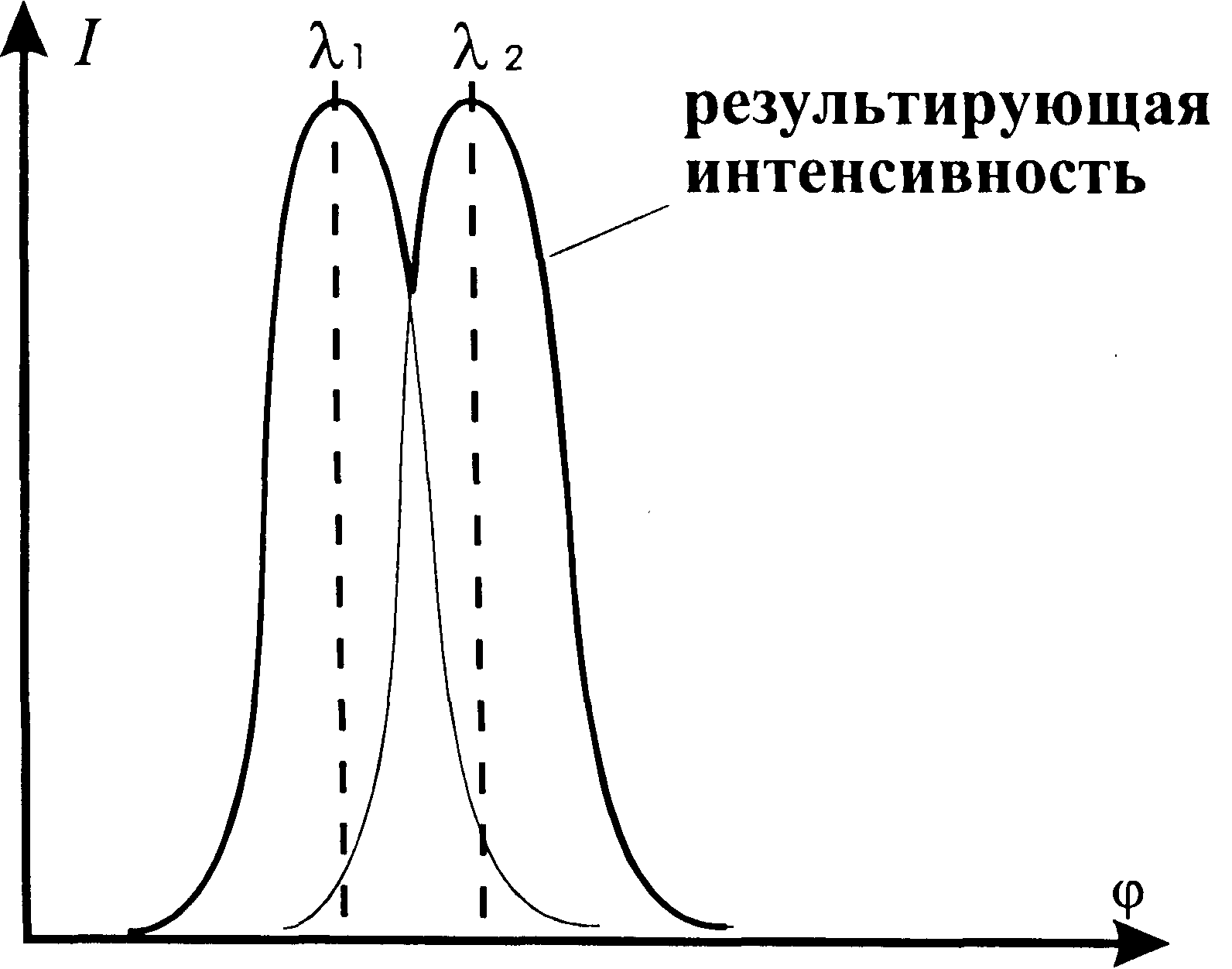
По предложению Рэлея, подтвержденному и проверенному опытом, принято считать разрешение полным, когда максимум интенсивности одной из линий совпадает с минимумом другой (рис. 3.28.2). Если максимумы располагаются ближе, чем показанные на рис. 3.28.2, изображения линий λ1 и λ2, сливаются в одну – линии не разрешаются. Когда максимумы разнесены дальше, линии уверенно разрешены.
Разрешающей способностью (или разрешающей силой) принято называть способность решетки дать увидеть раздельно на экране в области длин волн λ две длины волны, отличных друг от друга на Δλ. Разрешающая способность является величиной безразмерной. Чем она больше, тем более близкие по длине волны линии способен разрешить прибор. По критерию Релея разрешающая способность дифракционной решетки определяется порядком спектра и полным числом штрихов решетки
N:
R = kN. (3.28.6)





 У прозрачных решеток штрихи наносятся на поверхность прозрачной (как правило, стеклянной) пластины либо вырезаются в виде узких щелей в непрозрачном экране и наблюдение ведется в проходящем свете.
У прозрачных решеток штрихи наносятся на поверхность прозрачной (как правило, стеклянной) пластины либо вырезаются в виде узких щелей в непрозрачном экране и наблюдение ведется в проходящем свете. , (3.28.3)
, (3.28.3)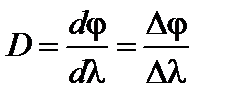 . (3.28.4)
. (3.28.4)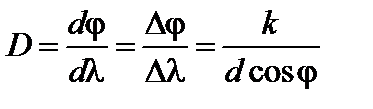 . (3.28.5)
. (3.28.5) Разрешающей способностью (или разрешающей силой) принято называть способность решетки дать увидеть раздельно на экране в области длин волн λ две длины волны, отличных друг от друга на Δλ. Разрешающая способность является величиной безразмерной. Чем она больше, тем более близкие по длине волны линии способен разрешить прибор. По критерию Релея разрешающая способность дифракционной решетки определяется порядком спектра и полным числом штрихов решетки N:
Разрешающей способностью (или разрешающей силой) принято называть способность решетки дать увидеть раздельно на экране в области длин волн λ две длины волны, отличных друг от друга на Δλ. Разрешающая способность является величиной безразмерной. Чем она больше, тем более близкие по длине волны линии способен разрешить прибор. По критерию Релея разрешающая способность дифракционной решетки определяется порядком спектра и полным числом штрихов решетки N:


