ПРИ ПОМОЩИ ДИФРАКЦИОННОЙ РЕШЕТКИ
Цель работы: изучение дифракции в сходящихся и параллельных лучах и определение длины волны света с помощью дифракционной решетки.
Теоретические положения
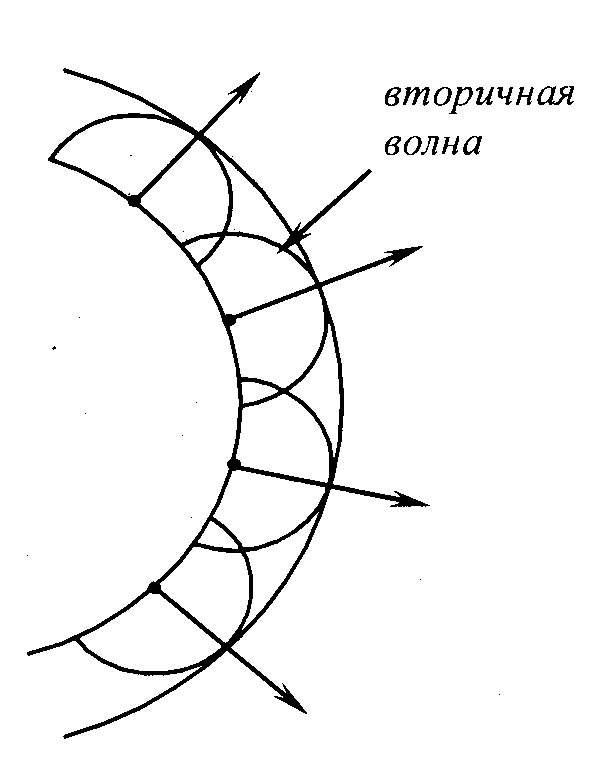 Рис. 3.5.1.
Рис. 3.5.1.
|
Дифракция света заключается в отклонении световых лучей от прямолинейного пути в случае прохождения их через малые отверстия или мимо малого непрозрачного экрана.
Дифракция обычно наблюдается, если размеры отверстия или препятствия одного порядка с длиной волны.
При расчетах дифракционных явлений пользуются особым приемом, который предложил Френель, называемый принципом Гюйгенса – Френеля и являющийся развитием принципа Гюйгенса.
Принцип Гюйгенса формулируется так: каждая точка волновой поверхности световых волн является источником вторичных волн. Огибающая поверхность вторичных волн будет новым положением волновой поверхности.
Принцип Гюйгенса решает задачу о распространении волнового фронта, но не решает задачу об интенсивности волн, которые идут в различных направлениях от источника.
Принцип Гюйгенса-Френеля рассматривает интенсивность результирующей волны как результат интерференции вторичных волн, являющихся когерентными, поскольку зарождаются на одном и том же фронте волны.
Рис. 3.5.2.
Интерференция вторичных волн, по Френелю, происходит следующим образом: пусть из точки S распространяется сферическая волна радиуса R. Выберем на этой поверхности элементарные площадки d S одинакового размера. Все они являются когерентными источниками и нормаль к каждой из них образует различные углы a с лучом, идущим в точку B перед фронтом волны.

Рис. 3.5.3.
Для упрощения расчета интенсивности света в точке B Френель предложил метод, получивший название метода зон Френеля.
Разобьем весь фронт волны на зоны, расстояние от которых до точки B отличается на  . Опишем их из точки B, как из центра, окружностями с радиусами
. Опишем их из точки B, как из центра, окружностями с радиусами
 .
.
 Рис. 3.5.4.
Рис. 3.5.4.
|
Площади зон можно считать одинаковыми, а значения амплитуд световой волны, приходящей в точку B от каждой последующей зоны, постепенно убывают. Ясно, что от двух соседних зон волны приходят в точку B в противофазе.
Метод зон Френеля позволяет объяснить различные случаи дифракции. Рассмотрим некоторые из них, а именно:
дифракцию Френеля или дифракцию в сходящихся лучах, когда на отверстие или препятствие падает сферический фронт волны, и
дифракцию Фраунгофера, или дифракцию в параллельных лучах – на отверстие падает плоский фронт волны.
Примером первого вида дифракции (дифракции Френеля) может быть дифракция на круглом отверстии.
Если в отверстии умещается четное число зон Френеля, то волны приходящие в точку B от соседних зон гасят друг друга, и в точке B будет наблюдаться минимум освещенности. Если в отверстии умещается нечетное число зон, то одна из зон останется нескомпенсированной и в точке B наблюдается максимум интенсивности света. При смещении на экране в различных направлениях от точки B отверстие будет вырезать то четное, то нечетное число зон Френеля. Благодаря этому на экране мы увидим дифракционную картину от круглого отверстия в виде светлых и темных колец.
Примером второго вида дифракции (дифракции Фраунгофера) является дифракция параллельных лучей на одной щели. Щелью называют длинное и узкое отверстие в непрозрачном экране со строго параллельными краями, ширина которого значительно меньше длины.
 Рис. 3.5.5.
Рис. 3.5.5.
|
Свет падает параллельным пучком перпендикулярно щели, так что колебания всех точек щели совершаются в одинаковой фазе. Лучи, дифрагирующие под углом j, будут собраны линзой в точке B экрана и интерферируют.
При j = 0 все волны придут в точку О в одинаковой фазе и усилят друг друга; на экране появится светлая полоса – центральный максимум.
Чтобы определить результат интерференции в точке B при j ¹ 0, разобьем открытый участок волновой поверхности (ширину щели) на ряд зон Френеля. В данном случае они представляют собой узкие полоски, параллельные краям щели. Проведем через точку А плоскость АD, перпендикулярную пучку дифрагирующих лучей. Оптические пути лучей от АD до точки B одинаковы, поэтому разность хода СD крайних лучей равна:
D = а sin j. (3.5.1)
Зоны Френеля делят D на соответствующее число участков. Каждой точке в нечетной зоне Френеля соответствует точка в четной зоне, колебания которой приходят в точку B в противофазе. Следовательно, в точке B, для которой в ширине щели укладывается четное число зон Френеля, волны гасят друг друга и на экране в этом месте будет темная полоса.
Т.о., условием минимума для одной щели будет:
 ,
,  , (3.5.2)
, (3.5.2)
В тех направлениях, для которых на ширине щели умещается нечетное число зон, будет наблюдаться наибольшая интенсивность света. Т.е., дифракционные максимумы наблюдаются в направлениях, определяемых условием:
 ,
, 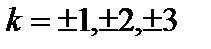 ,… (3.5.3)
,… (3.5.3)
k – порядок дифракционного максимума.
Распределение интенсивности света при дифракции на одной щели показано на рис. 3.5.5.
Итак, при освещении щели монохроматическим светом дифракционная картина представляет собой систему максимумов, симметричных относительно середины центрального максимума с быстрым убыванием интенсивности.
В случае освещения щели белым светом центральный максимум будет общим для всех длин волны, поэтому центр дифракционной картины – белая полоса.
Максимумы остальных порядков для разных длин волн уже не совпадают. Благодаря этому максимумы настолько расплывчаты, что сколько-нибудь отчетливого разделения длин волн (спектрального разложения) при помощи одной щели получить нельзя.
Рассмотрим более сложную дифракцию от двух щелей. В точке О по-прежнему будет светлая полоса (лучи от всех щелей приходят в одинаковой фазе).
В точке B на дифракционную картину от одной щели будет накладываться интерференция лучей, идущих от соответственных точек двух щелей. Минимумы будут на прежних местах, ибо те направления, по которым ни одна щель не посылает света, не получает его и при двух щелях.
Рис. 3.5.6.
Кроме этих минимумов возникают дополнительные минимумы в тех направлениях, в которых свет, посылаемый каждой из щелей, взаимно уничтожается. Из рис. 3.5.6 видно, что разность хода лучей D, идущих от соответствующих точек щелей, равна
 . (3.5.4)
. (3.5.4)
Дополнительные минимумы поэтому определяются условием:
 ;
;  (3.5.5)
(3.5.5)
Наоборот, в направлениях, где
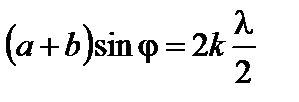 , (3.5.6)
, (3.5.6)
наблюдаются максимумы.
Из рис. 3.5.6 видно, что между двумя главными максимумами располагается один дополнительный минимум.
Итак, рассмотрение дифракции на двух щелях показывает, что в этом случае максимумы становятся более узкими и интенсивными.
Увеличение числа щелей делает это явление еще более отчетливым; интенсивность главных максимумов растет, а интенсивность побочных – падает.
Систему большого числа параллельных щелей называют
дифракционной решеткой.
Рис. 3.5.7.
Простейшая дифракционная решетка – это стеклянная пластинка, на которой с помощью делительной машины нанесены параллельные штрихи, непрозрачные для света.
Дифракционная картина от монохроматического света, прошедшего дифракционную решетку, наблюдается в фокальной плоскости линзы и представляет собой ряд светлых узких полос убывающей интенсивности, расположенных по обе стороны от центрального максимума k = 0 и разделенных широкими темными промежутками.
В случае если решетка освещена белым светом, лучи с различной длиной волны собираются в разных местах экрана. Поэтому центральный максимум имеет вид белой полосы, а остальные представляют собой окрашенные полоски, называемые дифракционными максимумами.
 Рис. 3.5.8.
Рис. 3.5.8.
|
В пределах каждого спектра окраска меняется от фиолетовой до красной. По мере увеличения порядка спектра последний становится шире, но интенсивность его уменьшается.
Соотношение, определяющее положения главных максимумов
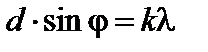 , (3.5.7)
, (3.5.7)
где d – постоянная решетки,  – порядок максимума (спектра), называется формулой дифракционной решетки.
– порядок максимума (спектра), называется формулой дифракционной решетки.
Эта формула позволяет определить длину световой волны по известному периоду решетки d, порядку спектра и экспериментальному углу j. Следовательно, с помощью дифракционной решетки можно разлагать свет на составные части и определять состав исследуемого излучения (определять длину волны и интенсивность всех его компонентов). Применяемые для этого приборы называются дифракционными спектрографами.
Описание оборудования
Приборы и принадлежности: осветитель, дифракционная решетка, экран с миллиметровым масштабом, измерительная линейка.
Рис. 3.5.9.
Для определения длины волны света с помощью дифракционной решетки на специальной рейке укрепляется решетка P и щель; штрихи решетки и щель располагаются параллельно. Щель освещается источником S. Перпендикулярно к оси рейки укрепляется миллиметровая линейка AB с подвижным указателем. Щель рассматривается через решетку глазом. На линейку проектируется изображение главных максимумов. На рис. 8 L – расстояние от дифракционной решетки до экрана, х – расстояние между серединами полос одного и того же цвета для спектров первого и второго порядка.
Порядок работы
1. Включить осветитель в сеть.
2. Установить экран на заданном расстоянии L от дифракционной решетки.
3. Замерить расстояние x между полосами заданного цвета в спектре первого порядка x 1 и второго порядка x 2. Проделать аналогичные измерения и вычисления для другого заданного цвета.
Обработка результатов
Для определения длины волны l по формуле (3.5.7)
необходимо учесть, что поскольку L >> х, то  и тогда
и тогда
 и
и  , (3.5.8)
, (3.5.8)
где k – порядок спектра, а постоянная решетки d = 0,01 мм. Вычислить среднее значение длины волны каждого цвета из двух значений, полученных из спектров первого и второго порядков. Сравнить полученные результаты с табличными значениями.
| k
| x 1
| x 2
| L
| λ1
| λ2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Ср. зн.
|
|
|
|
|
|
Контрольные вопросы
1. Что такое дифракция света?
2. В чем состоит метод Гюйгенса – Френеля и что такое зоны Френеля?
3. Как происходит дифракция в сходящихся лучах?
4. Как происходит дифракция в параллельных лучах (на одной щели)?
5. Почему нулевой максимум имеет наибольшую яркость? Почему он белый (при освещении белым светом)?
6. Как происходит дифракция в параллельных лучах на двух щелях?
7. Что такое дифракционная решетка и постоянная дифракционной решетки?
8. Какова причина возникновения дисперсии (спектра) света при использовании дифракционной решетки?
9. Выведите рабочую формулу.
Литература
1. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. – М.: КНОРУС, 2009, 576 с.
2. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.- 15-е изд., стереотип. – М.: Издательский центр «Академия», 2007. – 560 с.
3. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. – М: Высш. Шк., 1989. – 608 с.
ЛАБОРАТОРНАЯ РАБОТА № 3.6
ИЗУЧЕНИЕ ПОЛЯРИЗАЦИИ СВЕТА
Цель работы: экспериментальная проверка закона Малюса.
Теоретические положения
Поляризация света
Как известно, свет представляет собой электромагнитные волны. Векторы напряженности электрического и магнитного поля ( и
и  ) в каждый момент времени взаимно перпендикулярны и лежат в плоскости, перпендикулярной к направлению распространения волны (рис. 3.6.1).
) в каждый момент времени взаимно перпендикулярны и лежат в плоскости, перпендикулярной к направлению распространения волны (рис. 3.6.1).
Рис. 3.6.1.
Обычные источники света являются совокупностью огромного числа быстро высвечивающихся, за время около 10-7 – 10-8 секунд, элементарных источников (атомов и молекул), каждый из которых испускает волны с определенной ориентацией векторов  и
и  . Но элементарные источники испускают свет совершенно независимо друг от друга с разными фазами и с разной ориентацией векторов
. Но элементарные источники испускают свет совершенно независимо друг от друга с разными фазами и с разной ориентацией векторов  и
и  .
.
Световая волна с различной ориентацией 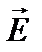 , а, следовательно, и
, а, следовательно, и  , называется естественным светом.
, называется естественным светом.
Векторы  и
и  в каждой точке волны пропорциональны по величине друг другу, поэтому состояние световой волны можно характеризовать значением одного из этих векторов, а именно
в каждой точке волны пропорциональны по величине друг другу, поэтому состояние световой волны можно характеризовать значением одного из этих векторов, а именно  .
.
Последнее целесообразно, поскольку именно вектор 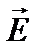 определяет фотоэлектрическое, фотографическое, зрительное и т. д. действия света.
определяет фотоэлектрическое, фотографическое, зрительное и т. д. действия света.
 Рис. 3.6.2.
Рис. 3.6.2.
|
В естественном луче колебания вектора  беспорядочно меняют направления, оставаясь в плоскости, перпендикулярной лучу (рис. 3.6.2 а).
беспорядочно меняют направления, оставаясь в плоскости, перпендикулярной лучу (рис. 3.6.2 а).
Если какое – либо направление колебаний  является преимущественным, то свет называется частично-поляризованным (рис. 3.6.2 б).
является преимущественным, то свет называется частично-поляризованным (рис. 3.6.2 б).
Если колебания вектора  могут совершаться лишь в одном определенном направлении в пространстве, то свет называется плоскополяризованным (рис. 3.6.2 в).
могут совершаться лишь в одном определенном направлении в пространстве, то свет называется плоскополяризованным (рис. 3.6.2 в).
Если же в плоскополяризованном луче колебания вектора 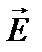 совершаются так, что его конец описывает круг, то свет называется поляризованным по кругу (рис. 3.6.2 г).
совершаются так, что его конец описывает круг, то свет называется поляризованным по кругу (рис. 3.6.2 г).
В плоскополяризованном луче плоскость колебаний вектора  называется плоскостью колебаний.
называется плоскостью колебаний.
Плоскость, проходящая через луч и вектор  , называется плоскостью поляризации.
, называется плоскостью поляризации.
Схематически естественный и плоско поляризованный луч можно изображать, как показано на рис. 3.6.3.
Существует несколько способов поляризации света. Приведем некоторые основные из них.
Рис. 3.6.3.





 Рис. 3.5.1.
Рис. 3.5.1.

 . Опишем их из точки B, как из центра, окружностями с радиусами
. Опишем их из точки B, как из центра, окружностями с радиусами .
. ,
,  , (3.5.2)
, (3.5.2) ,
, 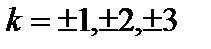 ,… (3.5.3)
,… (3.5.3) . (3.5.4)
. (3.5.4) ;
;  (3.5.5)
(3.5.5)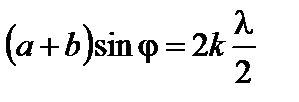 , (3.5.6)
, (3.5.6)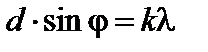 , (3.5.7)
, (3.5.7) – порядок максимума (спектра), называется формулой дифракционной решетки.
– порядок максимума (спектра), называется формулой дифракционной решетки. и тогда
и тогда и
и  , (3.5.8)
, (3.5.8) и
и  ) в каждый момент времени взаимно перпендикулярны и лежат в плоскости, перпендикулярной к направлению распространения волны (рис. 3.6.1).
) в каждый момент времени взаимно перпендикулярны и лежат в плоскости, перпендикулярной к направлению распространения волны (рис. 3.6.1). и
и  . Но элементарные источники испускают свет совершенно независимо друг от друга с разными фазами и с разной ориентацией векторов
. Но элементарные источники испускают свет совершенно независимо друг от друга с разными фазами и с разной ориентацией векторов  и
и  .
.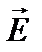 , а, следовательно, и
, а, следовательно, и  , называется естественным светом.
, называется естественным светом. и
и  в каждой точке волны пропорциональны по величине друг другу, поэтому состояние световой волны можно характеризовать значением одного из этих векторов, а именно
в каждой точке волны пропорциональны по величине друг другу, поэтому состояние световой волны можно характеризовать значением одного из этих векторов, а именно  .
.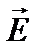 определяет фотоэлектрическое, фотографическое, зрительное и т. д. действия света.
определяет фотоэлектрическое, фотографическое, зрительное и т. д. действия света. беспорядочно меняют направления, оставаясь в плоскости, перпендикулярной лучу (рис. 3.6.2 а).
беспорядочно меняют направления, оставаясь в плоскости, перпендикулярной лучу (рис. 3.6.2 а). является преимущественным, то свет называется частично-поляризованным (рис. 3.6.2 б).
является преимущественным, то свет называется частично-поляризованным (рис. 3.6.2 б). могут совершаться лишь в одном определенном направлении в пространстве, то свет называется плоскополяризованным (рис. 3.6.2 в).
могут совершаться лишь в одном определенном направлении в пространстве, то свет называется плоскополяризованным (рис. 3.6.2 в).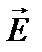 совершаются так, что его конец описывает круг, то свет называется поляризованным по кругу (рис. 3.6.2 г).
совершаются так, что его конец описывает круг, то свет называется поляризованным по кругу (рис. 3.6.2 г). называется плоскостью колебаний.
называется плоскостью колебаний. , называется плоскостью поляризации.
, называется плоскостью поляризации.


