1. Идемпотентность & и Ú: х & x = x, x Ú x = x.
2. Коммутативность &,Ú,Å,|,~, 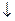 .
.
3. Ассоциативность &,Ú,Å,~, поэтому в формулах вида xyz можно не ставить никаких скобок.
4. Дистрибутивность:
а) & по отношению к Ú: x &(y Ú z)= xy Ú xz,
б) Ú по отношению к &: x Ú(y & z)=(x Ú y)&(x Ú z),
в) & по отношению к Å: x (y Å z)= xy Å xz.
5. Инволюция: 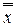 = х.
= х.
6. Правило де Моргана: 
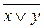 =
= 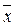 &
& 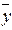 и
и 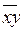 =
= 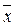 Ú
Ú 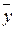 .
.
7. Законы действия с 0 и 1:
x Ú0= x, x Ú1=1, x Ú 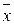 =1, x &0=0, x &1= x, x &
=1, x &0=0, x &1= x, x & 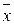 =0, x Å1=
=0, x Å1= 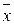 , x Å0= x.
, x Å0= x.
8. Самодистрибутивность импликации: x ®(y®z)=(x®y) ® (x®z).
Равенство всех этих формул доказывается по определению, т.е. по равенству функций, которые они реализуют.
Проверим для примера самодистрибутивность импликации: x ®(y ® z)=(x ® y) ®(x ® z).
| x
| y
| z
| y ® z
| x ®(y ® z)
| x ® y
| x ® z
| ®
|
|
|
|
|
|
|
|
|
|
При оперировании с функциями алгебры логики бывают полезны следующие эквивалентности (большинство из них называют обычно основными эквивалентностями алгебры логики). Построив таблицу для соответствующих функций, можно убедиться в справедливости следующих эквивалентностей:
1. 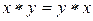 – коммутативность связки *, где символ * является общим обозначением для связок (операций) &, Ú, Å, ~, |, ¯.
– коммутативность связки *, где символ * является общим обозначением для связок (операций) &, Ú, Å, ~, |, ¯.
2. 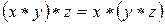 – ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.
– ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.
3. Дистрибутивность
а) 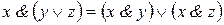 – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;
б) 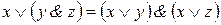 – дистрибутивность дизъюнкции относительно конъюнкции;
– дистрибутивность дизъюнкции относительно конъюнкции;
в) 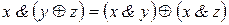 – дистрибутивность конъюнкции относительно сложения по mod 2 (по модулю два).
– дистрибутивность конъюнкции относительно сложения по mod 2 (по модулю два).
4. а) 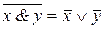 ; б)
; б) 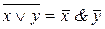 суть правила де Моргана;
суть правила де Моргана;
5. а) 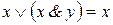 ; б)
; б) 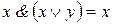 суть правила поглощения;
суть правила поглощения;
6. а) 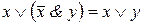 ; б)
; б) 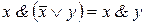 ;
;
7. а) 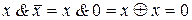 ; б)
; б) 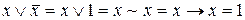 ;
;
в) 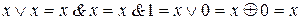 ; г)
; г) 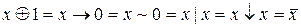 ; д)
; д) 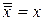 ;
;
8. а) 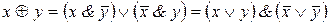 ;
;
б) 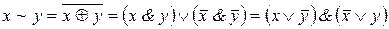 ; в)
; в) 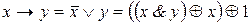 ;
;
9. а) 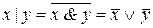 ; б)
; б) 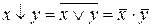 .
.
Следствия из свойств элементарных функций
1. Законы склеивания:
xy Ú x 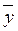 = x (y Ú
= x (y Ú 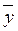 )= x
)= x 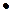 1= x (дистрибутивность & относительно Ú);
1= x (дистрибутивность & относительно Ú);
(x Ú y)&(x 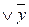 )= x
)= x 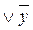 y = x Ú0= x (дистрибутивность Ú относительно &).
y = x Ú0= x (дистрибутивность Ú относительно &).
2. Законы поглощения:
x Ú xy = x (1Ú y)= x 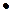 1= x; x &(x Ú y)= x Ú xy = x.
1= x; x &(x Ú y)= x Ú xy = x.
Свойства элементарных функций и теорема о замене подформул на эквивалентные позволяют упрощать формулы.
Пример 3: Упростим формулы:
1. x 2 x 3Ú x 1 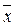 2 x 3 = x 3(x 2Ú x 1
2 x 3 = x 3(x 2Ú x 1 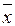 2) = x 3((x 2Ú x 1)&(x 2Ú
2) = x 3((x 2Ú x 1)&(x 2Ú 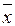 2)) = (x 1Ú x 2) x 3.
2)) = (x 1Ú x 2) x 3.
2. x 1Ú 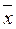 1 x 2Ú
1 x 2Ú 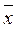 1
1 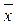 2 x 3Ú 1
2 x 3Ú 1 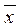 2 x 3 x 4 = x 1Ú
2 x 3 x 4 = x 1Ú 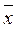 1(x 2Ú
1(x 2Ú 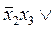
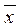 2
2 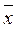 3 x 4) = x 1Ú
3 x 4) = x 1Ú 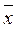 1 (x 2Ú x 3Ú
1 (x 2Ú x 3Ú 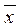 2
2 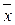 3 x 4) = (x 1Ú
3 x 4) = (x 1Ú 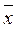 1 Ошибка! Ошибка внедренного объекта.)(x 1Ú x 2Ú x 3Ú
1 Ошибка! Ошибка внедренного объекта.)(x 1Ú x 2Ú x 3Ú 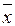 2
2 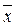 3 х 4) = x 1Ú(x 2Ú x 3)Ú(
3 х 4) = x 1Ú(x 2Ú x 3)Ú(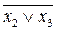 ) x 4 = x 1Ú(x 2Ú х 3Ú(
) x 4 = x 1Ú(x 2Ú х 3Ú(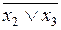 ))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.
))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.
Принцип двойственности
Определение 1. Функции f *(x 1,..., xn) называется двойственной к функции f (x 1,..., xn), если f *(x 1,..., xn) = 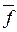 (
(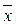 1,...,
1,..., 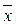 n).
n).
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
Функции f (x) = x и g (x) = 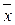 двойственны сами себе:
двойственны сами себе:
так как f *(0)= 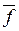 (1).
(1).
Определение 2. Если f *(x 1,..., xn) = f (x 1,..., xn), то f (x 1,..., xn) называется самодвойственной.
Пример 2. Покажем, что f (x 1, x 2, x 3)= x 1Å x 2Å x 3 – самодвойственна:
Если f *– самодвойственна, то 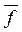 (
(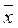 1,...,
1,..., 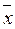 n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
Пример 3. Покажем, что функция х1Úх2 двойственна к x1&x2, функция х1 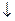 х2 двойственна к функции x1|x2.
х2 двойственна к функции x1|x2.
| x 1 x 2
| f = х 1Ú х 2
| f *
| g = x 1| x 2
| g *= x 1 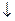 x 2 x 2
|
| 0 0
0 1
1 0
1 1
|
|
|
|
|
Теорема о двойственных функциях
Если f * двойственна к f, то f двойственна к f *.





 .
.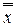 = х.
= х.
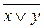 =
= 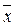 &
& 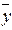 и
и 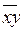 =
= 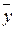 .
.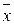 =1, x &0=0, x &1= x, x &
=1, x &0=0, x &1= x, x & 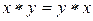 – коммутативность связки *, где символ * является общим обозначением для связок (операций) &, Ú, Å, ~, |, ¯.
– коммутативность связки *, где символ * является общим обозначением для связок (операций) &, Ú, Å, ~, |, ¯.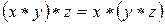 – ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.
– ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.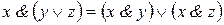 – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;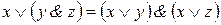 – дистрибутивность дизъюнкции относительно конъюнкции;
– дистрибутивность дизъюнкции относительно конъюнкции;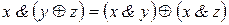 – дистрибутивность конъюнкции относительно сложения по mod 2 (по модулю два).
– дистрибутивность конъюнкции относительно сложения по mod 2 (по модулю два).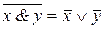 ; б)
; б) 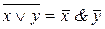 суть правила де Моргана;
суть правила де Моргана;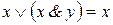 ; б)
; б) 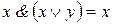 суть правила поглощения;
суть правила поглощения;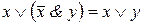 ; б)
; б) 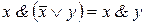 ;
;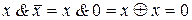 ; б)
; б) 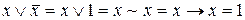 ;
;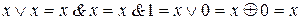 ; г)
; г) 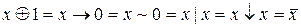 ; д)
; д) 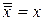 ;
;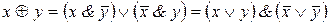 ;
;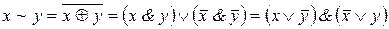 ; в)
; в) 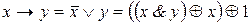 ;
;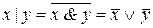 ; б)
; б) 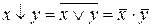 .
.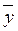 = x (y Ú
= x (y Ú 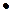 1= x (дистрибутивность & относительно Ú);
1= x (дистрибутивность & относительно Ú);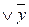 )= x
)= x 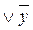 y = x Ú0= x (дистрибутивность Ú относительно &).
y = x Ú0= x (дистрибутивность Ú относительно &).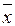 2) = x 3((x 2Ú x 1)&(x 2Ú
2) = x 3((x 2Ú x 1)&(x 2Ú 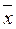 1 x 2Ú
1 x 2Ú 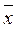 1
1 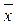 2 x 3Ú 1
2 x 3Ú 1 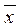 2 x 3 x 4 = x 1Ú
2 x 3 x 4 = x 1Ú 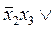
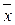 3 x 4) = (x 1Ú
3 x 4) = (x 1Ú 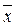 3 х 4) = x 1Ú(x 2Ú x 3)Ú(
3 х 4) = x 1Ú(x 2Ú x 3)Ú(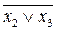 ) x 4 = x 1Ú(x 2Ú х 3Ú(
) x 4 = x 1Ú(x 2Ú х 3Ú(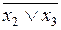 ))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.
))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.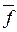 (
(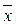 1,...,
1,..., 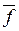 (1).
(1).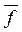 (
(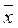 1,...,
1,..., 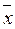 n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.


