Пусть функция f (x 1,…, xn) частично (не всюду) определена. Если f не определена на p наборах из 0 и 1, то существует 2 p возможностей для доопределения функции f. Полностью определенная функция g (x 1,…, xn) есть доопределение функции f, если g совпадает с f на тех наборах из 0 и 1, на которых f определена.
Задача минимизации частично определенной функции f сводится к отысканию такого доопределения g функции f, которое имеет простейшую (по числу букв) минимальную форму.
Обозначим через f 0(x 1,…, xn) и f 1(x 1,…, xn) доопределения нулями и единицами соответсвенно частично определенной функции f (x 1,…, xn).
Теорема. Минимальная ДНФ частично определенной функции f (x 1,…, xn) есть дизъюнкция самых коротких импликант в сокращенной ДНФ доопределения f 1(x 1,…, xn), которые в совкупности накрывают все конституенты единицы доопределения f 0(x 1,…, xn).
Доказательство. Рассмотрим СДНФ некоторого доопределения g (x 1,…, xn) функции f (x 1,…, xn). Конституенты единицы, входящие в эту форму, войдут и в СДНФ доопределения f 1. Поэтому любой простой импликант функции g будет совпадать с некоторым импликантом функции f 1 или накрываться им. Самые короткие импликанты, накрывающие единицы функции f, есть импликанты функции f 1. Доопределение f 0 имеет минимальное количество конституент единицы в своей СДНФ, следовательно, и количество простых импликант функции f 1, потребных для накрытия этих конституент, будет наименьшим. ДНФ, составленная из самых коротких простых импликант в сокращенной ДНФ функции f 1 , накрывающих все конституенты единицы функции f 0, будет самой короткой ДНФ, доопределяющей функцию f.
Так как единицы функции f 1 составлены из единиц функции f и единиц на наборах, на которых f не определена, то построенная ДНФ, накрывая все единицы функции f 0 (а, следовательно, и все единицы функции f), совпадает с минимальной ДНФ некоторого доопределения g функции f.
Алгоритм минимизации частично определенных функций
В классе ДНФ
1. Строим СДНФ функции f 0 .
2. Строим сокращенную ДНФ функции f 1 .
3. С помощью матрицы покрытий коституент единицы функции f 0 простыми импликантами функции f 1 и решеточного выражения строим все тупиковые ДНФ (для некоторых доопределений функции f).
4. Среди полученных ТДНФ выбираем простейшие, они являются минимальными ДНФ (для некоторых доопределений функции f).
Алгоритм минимизации частично определенных функций
В классе КНФ
Построение минимальных КНФ для частично определенной функции аналогично построению минимальных КНФ для всюду определенной функции.
Алгоритм минимизации частично определенных функций в классе нормальных форм аналогичен алгоритму минимизации в классе нормальных форм для всюду определенных функций.
Пример 1. В классе нормальных форм минимизировать частично определенную функцию f (x, y, z, t) = (1---010010-01--1)
Решение. Минимизируем функцию f в классе ДНФ.
1. Строим сокращенную ДНФ для доопределения единицами f 1 функции f по таблице 3.9.
Таблица 3.9
| x y z t
| f f 0 f 1 ` f h 0 h 1
|
| 0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
| 1 1 1 0 0 0
- 0 1 - 0 1
- 0 1 - 0 1
- 0 1 - 0 1
0 0 0 1 1 1
1 1 1 0 0 0
0 0 0 1 1 1
0 0 0 1 1 1
1 1 1 0 0 0
0 0 0 1 1 1
- 0 1 - 0 1
0 0 0 1 1 1
1 1 1 1 1 1
- 0 1 - 0 1
- 0 1 - 0 1
1 1 1 0 0 0
|

2. Строим матрицу покрытий коституент единицы в СДНФ для доопределения нулями f 0 функции f с помощью построенной сокращенной ДНФ для f 1 (таблица 3.10)
Таблица 3.10
3. По таблице строим решеточный многочлен
E = (2Ú4)(5Ú6)(3Ú4)(1Ú3)1 = 145 Ú 125 Ú 146 Ú 1236.
4. Строим все тупиковые ДНФ:
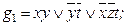


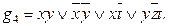
5. Из построенных тупиковых ДНФ выбираем минимальные:


Функции g 1 и g 3 есть минимальные доопределения функции f в классе ДНФ.
Минимизируем теперь функцию f в классе КНФ. Для этого проведем минимизацию функции ` f в классе ДНФ Пусть h 0 и h 1 есть доопределение нулями и единицами соответственно функции ` f.
Сокращенная ДНФ для
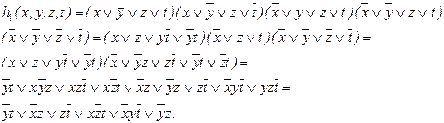
Матрица покрытия конституент единицы в СДНФ для h 0 с помощью простых импликант в сокращенной ДНФ для h 1 приведена в таблице 3.11.
Таблица 3.11
3. Решеточное выражение E =5 (2 Ú 3 Ú5) 2 (1Ú 4)(1Ú 6) = 25(1Ú 46) = 125 Ú 2446.
4. Строим две тупиковые ДНФ:
 и
и 
Минимальная. 
5. Функция  есть минимальное доопределение функции f в классе КНФ.
есть минимальное доопределение функции f в классе КНФ.
Найденные МДНФ g 1, g 3 и МКНФ  являются минимальными доопределениями функции f в классе нормальных форм.
являются минимальными доопределениями функции f в классе нормальных форм.
Техническая реализация минимальных форм для функции часто проще, а потому дешевле реализации ее СДНФ (СКНФ). Следовательно, этап минимизации при конструировании логических схем является одним из важнейших.













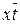



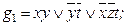


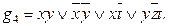


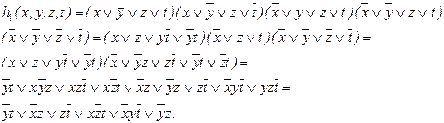




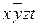




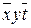

 и
и 
 есть минимальное доопределение функции f в классе КНФ.
есть минимальное доопределение функции f в классе КНФ. являются минимальными доопределениями функции f в классе нормальных форм.
являются минимальными доопределениями функции f в классе нормальных форм.


