Пусть f (x 1, …, xn) есть функция алгебры логики.
1. Построим СДНФ функции f, и пусть P 1, P 2, …, Pn есть ее коституенты единицы).
2. Построим сокращенную ДНФ функции, f и пусть K 1, K 2, …, Km – ее простые импликанты.
3. Построим матрицу покрытий простых импликант функции f ее конституентами единицы (табл. 3.4), полагая, что
+, если каждый множитель в Ki является множителем в Pj; (Pj есть aij = часть для Ki);
Æ в противном случае.
Таблица 3.4
| a. N
| P 1 P 2 … Pj … Pn
|
| K 1
K 2
Ki
Km
| a 11 a 12 … a 1 j …a 1 n
a 21 a 22 … a 2 j … a 2 n
ai 1 ai 2 … aij … ain
am 1 am 2 … amj … amn
|
4. Для каждого столбца j (1 £ j £ n) найдем множество Ej всех тех номеров I строк, для которых aij = 1. Пусть  Составим выражение
Составим выражение  Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …, m и с операциями & и Ú.
Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …, m и с операциями & и Ú.
5. В выражении A раскроем скобки, приведя выражение A к равносильному выражению  где перечислены все конъюнкции
где перечислены все конъюнкции  элементы
элементы 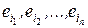 которой взяты из скобок 1,2,…, n соответственно в выражении A.
которой взяты из скобок 1,2,…, n соответственно в выражении A.
6. В выражении B проведем все операции удаления дублирующих членов и все операции поглощения. В результате получим дизъюнкцию элементарных конъюнкций C.
Утверждение. Каждая элементарная конъюнкция i 1& i 2&…& ir в С дает ТДНФ  для f. Все ТДНФ для функции f исчерпываются элементарными конъюнкциями в выражении С.
для f. Все ТДНФ для функции f исчерпываются элементарными конъюнкциями в выражении С.
Пример 5. Сокращенная ДНФ для функции f = (1111010010101111) имеет вид 
Для функции f построим все минимальные ДНФ.
1. Строим матрицу покрытий (таблица 3.5).
Таблица 3.5
|
|
| Конституенты единицы функции f
|
|
b. N
|
ПИ
|
x ` x ` x ` x ` x x x x x x x
y ` y ` y ` y y ` y ` y y y y y
z ` z z z ` z ` z z ` z ` z z z
t t ` t t t ` t ` t ` t t t t
|
|
| x y
` x ` y
` y ` t
x ` t
` x ` z t
y ` z t
| + + + +
+ + + +
+ + + +
+ + + +
+ +
+ +
|
2. Строим решеточное выражение (по столбцам таблицы).
E = (2Ú3)(2Ú5)(2Ú3)2(5Ú6)(3Ú4)(3Ú4)(1Ú4)(1Ú6)(1Ú4)(1)= (2Ú3)(2Ú5)(5Ú6)(3Ú4)(1Ú4)(1Ú6)12 = (5Ú6)(3Ú4)(1)(2) = 1235Ú1245Ú1236Ú1246.
3. Строим все тупиковые ДНФ функции f:
 простые импликанты(ПИ) 1,2,3,5;
простые импликанты(ПИ) 1,2,3,5;
 простые импликанты 1,2,4,5;
простые импликанты 1,2,4,5;
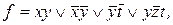 простые импликанты 1,2,3,6;
простые импликанты 1,2,3,6;
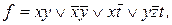 простые импликанты 1,2,4,6.
простые импликанты 1,2,4,6.
4. Все найденные ТДНФ являются минимальными ДНФ.
Алгоритм минимизации функций в классе ДНФ
1. Строим СДНФ функции f.
2. Строим сокращенную ДНФ функции f.
3. С помощью матрицы покрытий и решеточного выражения строим все ТДНФ функции f.
4. Среди построенных ТДНФ выбираем все минимальные дизъюнктивные нормальные формы функции f.
Алгоритм минимизации функций в классе КНФ
Чтобы построить все минимальные КНФ (МКНФ) функции f, следует построить все МДНФ функции ` f и взять от каждой из них отрицание, для чего заменить знаки & на Ú, а Ú на & (сохранив первоначальное распределение скобок) и над каждой буквой поставить знак отрицания. Полученные КНФ для функции f будут минимальными. В самом деле, если бы для f существовала КНФ с меньшим числом букв, то ее отрицание дало бы для ` f ДНФ с меньшим числом букв, чем в любой из минимальных ДНФ для ` f. Противоречие с их минимальностью.





 Составим выражение
Составим выражение  Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …, m и с операциями & и Ú.
Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …, m и с операциями & и Ú. где перечислены все конъюнкции
где перечислены все конъюнкции  элементы
элементы 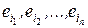 которой взяты из скобок 1,2,…, n соответственно в выражении A.
которой взяты из скобок 1,2,…, n соответственно в выражении A. для f. Все ТДНФ для функции f исчерпываются элементарными конъюнкциями в выражении С.
для f. Все ТДНФ для функции f исчерпываются элементарными конъюнкциями в выражении С.
 простые импликанты(ПИ) 1,2,3,5;
простые импликанты(ПИ) 1,2,3,5; простые импликанты 1,2,4,5;
простые импликанты 1,2,4,5;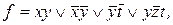 простые импликанты 1,2,3,6;
простые импликанты 1,2,3,6;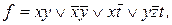 простые импликанты 1,2,4,6.
простые импликанты 1,2,4,6.


