

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Метод разделения переменных и метод функции источника (Грина) позволяют получать явное выражение для решения краевых задач только в случае областей простейшего вида. Сведение краевых задач для уравнения Лапласа или Пуассона при помощи поверхностных интегралов к интегральным уравнениям, с одной стороны, удобно для теоретического исследования вопроса существования и единственности решения краевых задач, а с другой стоны, создает возможность для эффективного численного решения краевых задач для областей сложной формы.
Сформулируем внутренние краевые задачи для некоторого контура С.
Найти функцию u, гармоническую в области Т, ограниченной контуром С, и удовлетворяющие на этом контуре граничным условиям:
 для первой краевой задачи
для первой краевой задачи
или
 для второй краевой задачи
для второй краевой задачи
Аналогично ставятся и внешние краевые задачи, причем при постановке второй краевой задачи как внутренней, так и внешней, в граничном условии нормаль будем считать внутренней.
Будем искать решение первой внутренней краевой задачи в виде потенциала двойного слоя
 , (24)
, (24)
где 
Как мы помним, функция W (M) разрывна на контуре С, поэтому для обеспечения непрерывности решения, в качестве граничного условия нужно взять W в(Р 0), т.е.

Тогда формулу (17) §6, можем записать в виде

При этом W (P 0) имеет вид

В результате окончательно можно записать
 (25)
(25)
Это есть не что иное как уравнение для нахождения ν (Р). Если обозначить через s 0 и s дуги контура С, отсчитываемые от некоторой начальной точки до точек Р 0 и Р, то это уравнение можно записать в следующем виде
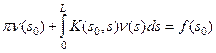 (26)
(26)
где L – длина контура С.
Это уравнение является интегральным уравнением Фредгольма второго рода. Получив в результате решения интегрального уравнения функцию ν (s) или, что тоже самое, ν (Р), мы можем записать решение задачи в виде Функция переменных K (s 0, s) называется ядром этого уравнения и имеет вид
|
|
 (27)
(27)
Для внешней краевой задачи мы для обеспечения непрерывности решения мы должны во второй формуле (17) подставить граничное условие f (P 0) вместо W в(Р 0). Тогда после перехода к переменной s получим
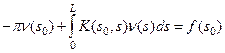 (28)
(28)
При решении второй краевой задачи (по-прежнему для случая двух переменных) мы будем искать решение в виде потенциала простого слоя
 (нормаль внутренняя) (29)
(нормаль внутренняя) (29)
Функция V (M) непрерывна на контуре С, однако граничное условие второй краевой задачи содержит производную по нормали, которая для V (M) терпит в точке Р 0 разрыв, описываемый в случае внутренней нормали формулой
 (30)
(30)
Для обеспечения непрерывности решения внутри области, в качестве граничного условия нужно взять  , т.е.
, т.е.

Теперь условие разрыва, описываемoе первой формулой в (28) можем переписать в виде

где функция  имеет вид
имеет вид

В результате окончательно можно записать
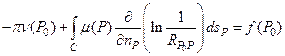 (31)
(31)
Уравнение для нахождения μ (Р). Обозначая, как и раньше, через s 0 и s дуги контура С, отсчитываемые от некоторой начальной точки до точек Р 0 и Р, можем записать это уравнение в следующем виде
 (32)
(32)
Для внешней задачи получим аналогичное интегральное уравнение
 (31)
(31)
где  – ядро интегрального уравнения Фредгольма второго рода. Это уравнение служит для определения плотности μ (s), знание которой позволит нам записать решение задачи в виде
– ядро интегрального уравнения Фредгольма второго рода. Это уравнение служит для определения плотности μ (s), знание которой позволит нам записать решение задачи в виде
Легко видеть, что ядро  можно получить из ядра K (s 0, s), поменяв местами переменные s 0 и s, т.е.
можно получить из ядра K (s 0, s), поменяв местами переменные s 0 и s, т.е.
 = K (s, s 0)
= K (s, s 0)
Такие ядра называются взаимно сопряженными.
Задача Дирихле для круга
Если контур С является окружностью радиуса R, то внутренняя нормаль в точке Р направлена по диаметру, а значит
 , (32)
, (32)
 так как φ – есть угол Р 0 РР ' (Рис. 36). Тогда интегральное уравнение для функции ν (s 0) принимает вид
так как φ – есть угол Р 0 РР ' (Рис. 36). Тогда интегральное уравнение для функции ν (s 0) принимает вид
 (33)
(33)
Нетрудно убедиться, что его решением будет функция
|
|
 (34)
(34)
где А – некоторая постоянная, которую мы определим, подставляя выражение для ν (s) (34) в интегральное уравнение (33)
 ,
,
откуда находим для постоянной А выражение через заданную функцию f (s)

Таким образом, функция
 (35)
(35)
является решением интегрального уравнения (33).
Соответствующий потенциал двойного слоя будет равен

Преобразуем правую часть этой формулы, предполагая, что М лежит внутри С:
 (36)
(36)
Из Δ ОРМ (Рис. 37) видно, что

 , (37)
, (37)
так как

Подставляя теперь формулу (37) для К в формулу (36), мы получим уже знакомый нам интеграл Пуассона (§ 11, Гл. VI)

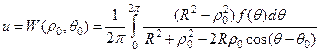 , (38)
, (38)
дающей решение задачи Дирихле для круга.
Замечание. Проведенные в этом параграфе рассуждения показывают, что при любой непрерывной функции f формула (37) определяет гармоническую функцию, непрерывно примыкающую к граничным значениям f.
Г л а в а. VIII. Уравнение Гельмгольца
|
|
|

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!