Проекция результирующей силы, действующей на МТ массой m, определяется с помощью второго закона Ньютона:

 Из уравнения следует, что координата х=0 определяет положение равновесия точки (
Из уравнения следует, что координата х=0 определяет положение равновесия точки ( ), а при
), а при  сила F пропорциональна смещению х из положения равновесия и направлена в сторону, противоположную этому смещению, т.е. положению равновесия.
сила F пропорциональна смещению х из положения равновесия и направлена в сторону, противоположную этому смещению, т.е. положению равновесия.


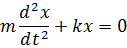



-Дифференциальное уравнение свободных гармонических колебаний.
Решение такого уравнения записывается в виде:

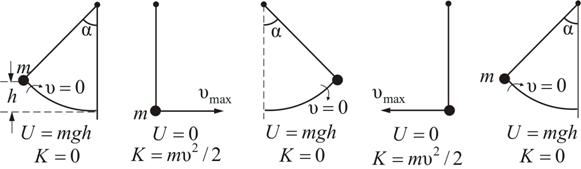
 При совершении колебаний между элементами системы происходит перераспределение энергии.
При совершении колебаний между элементами системы происходит перераспределение энергии.




 - дифференциальное уравнение.
- дифференциальное уравнение.
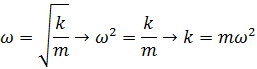


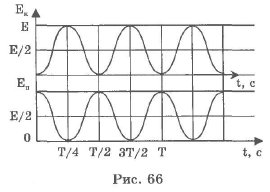
Полная механическая энергия осциллятора сохраняется:

Т.е. энергия, которой обладает колебательная система, независима от её природы.
Формы представления гармонических колебаний. Простые осцилляторы (физический, математический и пружинный маятники).
Гармонические колебания – колебания, для которых закон движения некоторой физической величины х может быть записан как некоторая функция от cos или sin.
Способы представления:
1. Аналитический способ – способ записи в виде зависимости от cos или sin.


2.  Графический способ
Графический способ
3.  Метод векторных диаграмм
Метод векторных диаграмм






4. 

 .
.
Осциллятор - система способная совершать колебательное движение. Колебания в осцилляторе возникают, когда ему сообщается некоторая энергия.
Физический маятник – твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через центр О, который не совпадает с центром масс.



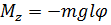



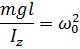

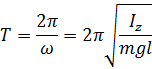
Математический маятник – идеализированная система, состоящая из материальной точки массой m, подвешенной на тонкой невесомой нерастяжимой нити длиной  и способной осуществлять колебания под действием силы тяжести
и способной осуществлять колебания под действием силы тяжести  .
.




 Пружинный маятник –материальная точка массой m, подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жёсткостью k и совершающая гармонические колебания под действием силы упругости.
Пружинный маятник –материальная точка массой m, подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жёсткостью k и совершающая гармонические колебания под действием силы упругости.




 Собственная частота осциллятора.
Собственная частота осциллятора.


Сложение колебаний методом векторных диаграмм. Биения.
 Рассмотрим сложение двух гармонических колебаний, которые распространяются в одном и том же направлении.
Рассмотрим сложение двух гармонических колебаний, которые распространяются в одном и том же направлении.
Имеем некоторое колебание с координатой 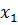 и амплитудой
и амплитудой  :
:

и колебание с координатой  и амплитудой
и амплитудой  :
:
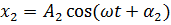
 – одинакова для двух колебаний.
– одинакова для двух колебаний.


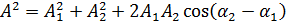


α – начальная фаза суммарного колебания.
Если разность фаз – это целое число колебаний, то cosα=0, а амплитуда максимальна 

Если же  , то колебания происходят в разных фазах и амплитуда минимальна
, то колебания происходят в разных фазах и амплитуда минимальна  .
.
Есть 2 колебания с частотами  , причём
, причём  ;
; 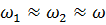 ;
;  амплитуда одинакова.
амплитуда одинакова.

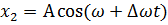


Амплитуда колебаний будет меняться со временем и в результате мы получим явление биения.
 В результате сложения двух колебаний с близкими частотами формируется колебание, амплитуда которого будет меняться по периодическому закону.
В результате сложения двух колебаний с близкими частотами формируется колебание, амплитуда которого будет меняться по периодическому закону.







 Из уравнения следует, что координата х=0 определяет положение равновесия точки (
Из уравнения следует, что координата х=0 определяет положение равновесия точки ( ), а при
), а при  сила F пропорциональна смещению х из положения равновесия и направлена в сторону, противоположную этому смещению, т.е. положению равновесия.
сила F пропорциональна смещению х из положения равновесия и направлена в сторону, противоположную этому смещению, т.е. положению равновесия.

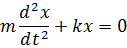





 При совершении колебаний между элементами системы происходит перераспределение энергии.
При совершении колебаний между элементами системы происходит перераспределение энергии.



 - дифференциальное уравнение.
- дифференциальное уравнение.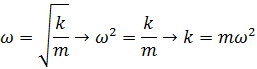





 Графический способ
Графический способ Метод векторных диаграмм
Метод векторных диаграмм







 .
.


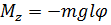



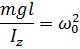

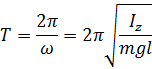
 и способной осуществлять колебания под действием силы тяжести
и способной осуществлять колебания под действием силы тяжести  .
.



 Пружинный маятник –материальная точка массой m, подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жёсткостью k и совершающая гармонические колебания под действием силы упругости.
Пружинный маятник –материальная точка массой m, подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жёсткостью k и совершающая гармонические колебания под действием силы упругости.



 Собственная частота осциллятора.
Собственная частота осциллятора.

 Рассмотрим сложение двух гармонических колебаний, которые распространяются в одном и том же направлении.
Рассмотрим сложение двух гармонических колебаний, которые распространяются в одном и том же направлении.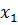 и амплитудой
и амплитудой  :
:
 и амплитудой
и амплитудой  :
: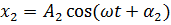
 – одинакова для двух колебаний.
– одинакова для двух колебаний.

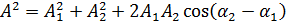




 , то колебания происходят в разных фазах и амплитуда минимальна
, то колебания происходят в разных фазах и амплитуда минимальна  .
. , причём
, причём  ;
; 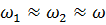 ;
;  амплитуда одинакова.
амплитуда одинакова.
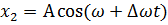


 В результате сложения двух колебаний с близкими частотами формируется колебание, амплитуда которого будет меняться по периодическому закону.
В результате сложения двух колебаний с близкими частотами формируется колебание, амплитуда которого будет меняться по периодическому закону.


