Понятие о статистических распределениях Ферми-Дирка и Бозе-Эйнштейна. Переход к классическому распределению при высоких температурах.

Статистические распределения.
Как и в квантовой физике в статистическ. физике закономерности имеют вероятностный характер.
Функция распределения Больцмана – функция распределения для классической статистики. И согласно принципу соответствия она должна являться предельным случаем статистического распределения, в который переходят квантово-стат. распредел.
Квантово-статистических распределений два – это обусловлено принципом неразделимости тождественных частиц, согласно которому есть 2 типа волновых функций: симметричное- Ψ(-Х)=Ψ(Х); ассиметричные волновые функции- Ψ(-Х)=-Ψ(Х). Различие в симметрии приводит к тому, что частицы ведут себя по-разному.
В любом статистическом подходе все допустимые состояния являются равновероятными.
Различия между 2-мя стат. распределениями заключается в различных способах определения микросостояний и статистических весов.
В классической статистике Больцмана тождественные частицы принципиально различимы.
В квантовой статистике тождественные частицы принципиально неразличимы.

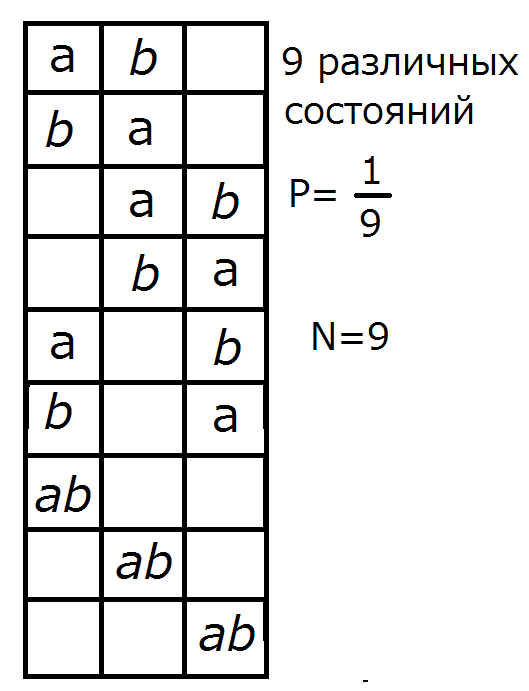
Различие на два статистических подхода делается по величине спинового квантового числа (спина).
Частицы с полуцелым спином – фермионы – подчиняются статистическому распределению Ферми-Дирка.
Частицы с целочисленным спином – бозоны – подчиняются статистическому распределению Бозе-Эйнштейна.
Рассмотрим 2 частицы, которые могут занимать какие-либо из 3-х возможных состояний.
Основной задачей при анализе статистического распределения является:
1. Нахождение функции распределения частиц по определённым параметрам (направление, по энергии).
2. Определение средних значений физических величин, которые характеризуют наиболее вероятные средние значения макросистем физических частиц.
Рассмотрение делается для частиц, которые представл. как частицы, находящиеся в 6D пространстве (х,y,z-3 декартовые,p_x,p_y,p_z - значения импульса вдоль осей координат), называемым фазовым пространством.
Состояние системы определяется тем, как в этом пространстве определяются точки, которые соответствуют состоянию всех n-частиц. Поскольку ∆х· ∆p_x∆≥h В этом фазовом пространстве каждому положению частицы соответствует область пространства – фазовая ячейка.
Объём фазовой ячейки δΛ= ∆х· ∆y· ∆z· ∆p_x· ∆ p_y · ∆ p_z =h³.
Если в качестве параметра характ. состояния системы, взять энергию частицы ε_i, то можно записать некоторые функции распределения f(ε_i), которые будут определять среднее число частиц в 1 фазовой ячейке с величиной энергии ε_i.
Ф-Д: ; Б-Э: ; μ- величина хим. потенциала – величина которого находится из условия нормировки, т.е. сумма число всех частиц .
Для квантовых частиц наблюдается различные функцион. зависимости.
В каждой ячейке не может быть не более чем частица.
Ф-Д: μ(Т≠0)=ε_Р
В случае стат. Б-Э: при приближении Т к 0 и уменьшению энергии, число заполнения (число распределения) очень быстро возрастает. Наблюдаемое явление получило название Бозе-конденсация.
Если рассматривать случай классической статистики, т.е. статистика которая описывает поведение классической частицы в макроскопической системе число частиц велико и энергии отдельных частиц расположены так плотно, что их можно рассмотреть как результат непрерывного распределения.
Если f(ε_i)<<1 происходит размазывание всех частиц по всем возможным состояниям, т.е. число заполнения каждого из состояний стремится к 0.
В этом случае при анализе сопротивления можно пренебречь единицей. В результате получим (для больших температур): .
При большом изменении температуры μ<<ε⇒ .

63. Изотерма реального вещества. Понятие фазового перехода. Тройная точка. Критическая точка. Фазовые переходы 1-го и 2-го рода. Правило фаз Гиббса.
,
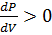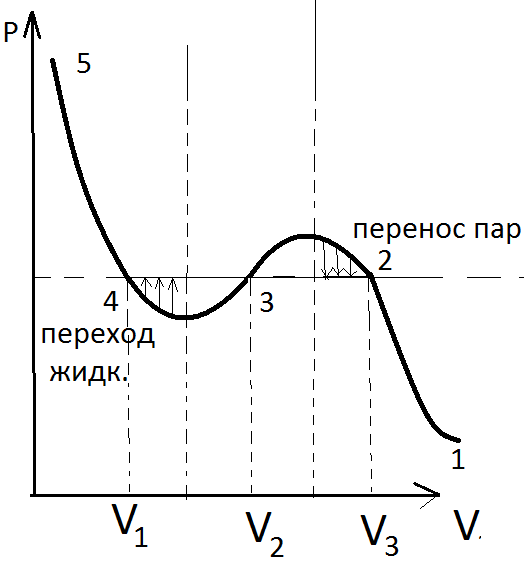
1-2, 4-5 Изотерма реального вещества
2-3-4 соответствует переход из газа в жидкость.
Длинна дуги 2-3 = длине дуги 3-4.

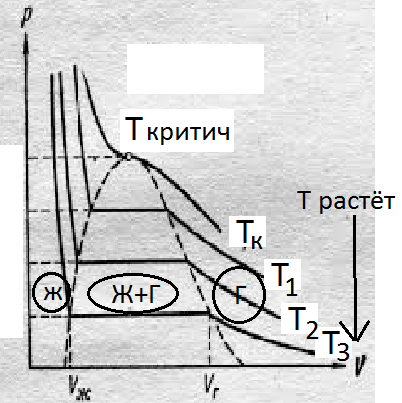Если построить набор изотер при различных температурах, начиная с критической, то набор изотерм, которые получ., позволяет определить области, в которых мы можем получить либо фазовое состояние, либо несколько.
Фазовая диаграмма: показывает условия для наблюдения той или иной фазы при определённых термодинамических условиях.
Критическая точка — сочетание значений температуры и давления (или, что эквивалентно, молярного объёма), при которых исчезает различие в свойствах жидкой и газообразной фаз вещества. В критической точке Тк различия между жидкостью и газом ищезают.
В критической точке плотность жидкости и её насыщенного пара становятся равны, а поверхностное натяжение жидкости падает до нуля, поэтому исчезает граница раздела фаз жидкость-пар.

Понятие фазового перехода.
Фаза – физически однородная часть системы, свойства которой отличны от других её частей, и отдалённая от них чётно выраженной границей.
1- газ при очень низком давлении,
1-2 изотермически сжимаем,
2-3 превращение газа в жидкость (конденсация),
3-2 испарение,
3-4 изотермически сжимаем,
4-5 из жидк. в тв. (кристаллизация),
5-4 плавление,
5-6 изотермически сжимаем.
Горизонтальные участки описывают области фазового перехода.

Фазовый переход - переход некоторого количества вещества из одной формы в другую на границе раздела (кривая – граница раздела 2-х фаз).
Переход из одной фазы в другую сопровождается поглощением либо выделением некоторого количества теплоты, которое называется скрытой теплотой перехода.
Такие переходы, в которых выделяется или поглощается тепло, называются фазовыми переходами 1-го рода ∆Q≠0, ∆V≠0 ( исключение: ρ=900кг/м³ ).
Фазовые переходы 2-го рода: в них изменение количества теплоты не происходит и объём, как правил, остаётся тем же самым ∆Q=0, ∆V=0.
К ФП 1-го рода относят переходы между несколькими кристаллическими структурами одного вещества (полиморфные структуры) полиморфизм.
ФП 2-го рода: переходы, которые можно получить, двигаясь по границе раздела двух фаз, и переход происходит в критической точке.

В одной единственной точке при уникальном наборе термодинамических параметров (Р,Т,V) могут существовать три фазы.
Тройная точка — точка соответствующая устойчивому равновесию трёх фаз.
q – удельная теплота фазового перехода Q=mq.
Теплота при: сублимации и возгонке, плавлении и кристаллизации, конденсации и испарении – попарно одинаковы.
Правило фаз Гиббса: С=К-Ф+2 где С – количество независимых степеней свободы (не может быть отрицательным), К – число компонентов в системе (сколько различных веществ она содержит), Ф – количество фаз, которые набл наблюдаются при данных условиях в системе.