Вынужденные колебания. Резонанс. Дифференциальное уравнение вынужденных колебаний.

Вынужденные колебания – движение колебательной системы под действием внешней периодической силы.

На материальную точку в инерциальной системе действуют

· возвращающая сила

· сила сопротивления среды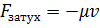

· вынуждающая внешняя сила .

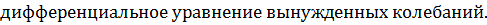
Закон, которому подчиняются колебания: амплитуда зависит от частоты вынуждающей силы; начальная фаза – функция частоты вынуждающей силы.

Метод векторных диаграмм.

Эти величины не являются постоянными, зависят от частоты собственной и частоты вынужденной.

Очевидно, что зависимость амплитуды от частоты внешней вынуждающей силы должна иметь некий экстремум, при совпадении собственной частоты и вынужденной частоты функция будет иметь максимум.

Резонанс - явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты осциллятора с вынуждающей частотой.

Условия резонанса:

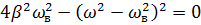
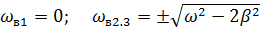
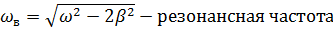
При резонансной частоте наблюдается максимальное значение амплитуды.

Амплитудно-частотная характеристика(АЧХ) является по своей сути функцией, показывающей зависимость на выходе амплитуды от частоты гармонического сигнала на входе.

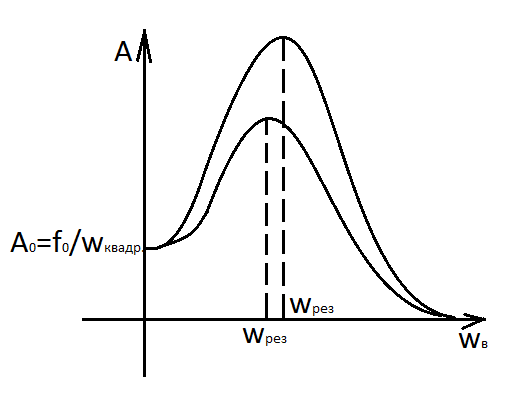
В зависимости от величины затухания положение максимума будет меняться как по амплитуде, так и по частоте.

В предельном случае, если затухание много меньше , то отношение не что иное как добротность. . Добротность Q – это отношение запасённой (сообщённой) энергии осциллятором к энергии, которую он расходует на совершение одного колебания.

 

31. Волновое движение. Уравнение плоской бегущей волны. Волновое уравнение.
Колебания частиц среды, которые распространены в пространстве в течение времени называется волновым процессом или волной.
Любая волна, независимо от её природы переносит энергию, но не переносит вещество.
Различают: продольные волны - колебания совершаются в том же направлении, что и направление распространения волны (деформация в твёрдых телах, жидкостях, газах). Поперёчные волны – колебания совершаются в направлении, перпендикулярном направлению волны. В твёрдых телах может наблюдаться деформация сдвига поперёчной волны.
Фронт волны – геометрическое место точек в пространстве, до которого возмущение, передаваемое волной, распространяется за какой-то промежуток времени t.
Волновая поверхность – геометрическое место точек среды, которые совершают колебания в одинаковой фазе.
Волновая поверхность и фронт волны всегда перпендикулярны направлению распространения волны, которое можно назвать понятием луч.
Длинна волны λ -расстояние, на которое перемещается волна за время одного колебания.

Рассмотрим два предельных вида волн: плоские и сферические.
Плоские характеризуются фронтом с бесконечно большим радиусом кривизны, плоским фронтом и амплитудой, которая с течением времени не изменяется.
Сферическая волна – сферическая форма волн фронта, имеют точечный источник, амплитуда убывает по мере увеличения расстояния от волнового фронта до источника.

Рассмотрим первый тип волн – бегущие волны.
Плоская бегущая волна которая имеет определённую частоту ω.
S=S(x; t). Уравнение плоской волны:

В случае сферической волны: при распространении сферической волны, протяжённость волнового фронта увеличивается, энергия, которую переносит волна, распространяется по большому пространству, амплитуда по мере удаления от источника уменьшается.

В декартовых координатах волновое уравнение:
Скорость распространения зависит от процессов, в которые вовлечены частицы среды.
Скорость распространения продольной волны:
Для волновых процессов справедлив принцип суперпозиции: при распространении волны в среде нескольких волн колебания точек среды определяется суммой колебаний, которые совершили бы частицы среды при распространении каждой из волн в отдельности.
32. Стоячие волны. Уравнение стоячей волны. Спектр частот колебаний струны.

Колебания частиц среды, которые распространены в пространстве в течение времени называется волновым процессом или волной.
Любая волна, независимо от её природы переносит энергию, но не переносит вещество.

Длинна волны λ -расстояние, на которое перемещается волна за время одного колебания.

В простом случае стоячая волна может быть смоделирована как результат сложения двух бегущих волн с одинаковой частой, идущих в противоположном направлении.

 

 

Амплитуда колебаний – функция, зависящая только от координат.
Точки, в которых амплитуда колебаний = 0, - узлы.
Точки, в которых амплитуда колебаний max, - пучности.
Узел: S=0, coskx=0, kx=π/2, х=(2n+1) π/2; n=0,1,…
Пучности: Smax coskx=1, kx=0;π, x=πn, n=0,1,…

Если мы ограничим длину пространства в которое складывается 2 волны, которые распространяются навстречу друг другу.
Если ограничить пространство, то амплитуда должна быть одинаковой.

На границе раздела должны быть узлы, т.о. мы неким образом ограничиваем набор длин волн, которые могут быть в этой области пространства. И длинна волны соотносится с длинной этого пространства с помощью соотношения λ=2L/n.

λ/ϑ=Т=1/ν, ν=ϑ/λ, ν=nϑ/2L
Стоячие волны - пример макроскопической системы с квантованием частот.