Раньше других разделов физики стала развиваться механика. Механика есть наука о движении и равновесии тел. В широком смысле слова движение материи есть всякое ее изменение. Однако в механике под движением понимается только простейшая его форма, а именно перемещение тела относительно других тел. Принципы механики были впервые сформулированы Ньютоном (1643— 1727 гг.) в его основном труде "Математические начала натуральной философии" (1687 г.).
Различают три вида механического движения: поступательное, вращательное и колебательное.


 Поступательное движение – это движение, при котором все точки тела движутся по параллельным траекториям.
Поступательное движение – это движение, при котором все точки тела движутся по параллельным траекториям.
Вращательное движение – это движение, при котором точки тела движутся по концентрическим окружностям или дугам концентрических окружностей.
Колебательное движение – это движение, при котором тело, выйдя из положения равновесия, периодически возвращается к нему.
После Ньютона механика начала быстро развиваться, однако до начала XX века это развитие шло в основном в направлении совершенствования математических методов механики и применения ее законов ко всё новым и новым областям знания. Несомненные в то время успехи механики привели к представлению, что законов механики достаточно для объяснения всех явлений природы (механистический взгляд на природу вещей).
Положение в корне изменилось с открытием электрических и магнитных явлений, особенно с открытием электромагнитных волн. Окончательный отказ от механистических представлений произошел в начале XX века. Первое, что выяснилось, — это то, что механика Ньютона применима лишь к сравнительно медленным движениям со скоростями, заметно меньшими скорости света в вакууме с к= 300000 км/с. Движения, скорости которых приближаются к скорости света, называют релятивистскими.
Но скорость света огромна. В повседневной жизни мы имеем дело со скоростями, заметно меньшими.
Второе ограничение классической механики заключается в ее неприменимости к описанию явлений микромира, то есть к движениям тел малой массы в малых участках пространства. Более общей наукой, описывающей такие движения, является квантовая механика.
Таким образом, классическая механика Ньютона изучает медленные движения макроскопических тел.
Что такое движение и как его описывать? На этот вопрос отвечает кинематика, описывающая движение тел.
Кинематика – раздел механики, изучающий движение материальных тел в пространстве и времени без рассмотрения причин, вызывающих это движение.
Движение — это перемещение тела относительно других тел (изменение его положения в пространстве).
Таким образом, описывая движение тела, мы всегда привязываемся к какой-то координатной системе, относительно которой тело движется, или к системе отсчета. Движение тела определяется движением всех его точек (маленьких кусочков тела), поэтому мы начнем с описания движения материальной точки.
Материальной точкой называется тело, размерами которого можно пренебречь, считая, что вся масса тела сосредоточена в одной точке.
Прежде всего, выберем систему координат. Самая простая система — это декартова система координат, три взаимно перпендикулярных оси х, у, z.
3аконыприроды, очевидно, должны быть записаны в форме, которая не зависит от выбора системы координат. Мы для определенности будем пользоваться правой системой. Положение точки в выбранной нами системе координат задается радиус-вектором r, проекции которого на оси координат равны соответственно х, у, z. Таким образом, вектор r вполне однозначно определяется заданием трех его проекций, хотя это могут быть и другие три числа.
Если ввести три единичных вектора i, j, k, направленные вдоль координатных осей (единичные орты), то радиус-вектор r можно представить в виде суммы трех векторов:
r =x i +y j +z k.
В итоге мы приходим к известному результату, что квадрат длины вектора равен сумме квадратов его проекций:
r2=x2+y2+z2.
 Рассмотрим теперь движение материальной точки, траектория которой изображена на рис, 2.1, и определим такие важные для дальнейшего понятия, как скорость материальной точки υ и ускорение а.
Рассмотрим теперь движение материальной точки, траектория которой изображена на рис, 2.1, и определим такие важные для дальнейшего понятия, как скорость материальной точки υ и ускорение а.
Пусть радиус-вектор материальной точки в момент времени t1 равен r1: а в момент времени t2 равен r2. Таким образом, при движении радиус-вектор r изменяется со временем, иными словами, он является функцией времени r = r(t). Если нам известен закон этого изменения, то мы знаем, где в каждый момент времени находится материальная точка, то есть мы знаем закон ее движения. Задание функции r(t) эквивалентно заданию трех функций x(t), y(t) и z(t) — координат материальной точки, поскольку
r(t) = x(t)i + y(t)j + z(t)k. (2.2)
Разность векторов Dr = r2 – r1 называется перемещением материальной точки. Очевидно, что это тоже вектор, и он направлен из точки 1 в точку 2. Ясно, что
r1 + Dr12 = r1 + (r2-r1) = r2, (2.3)
Отношение перемещения материальной точки D r2 к интервалу времени Dt 12, то есть Dr 12 / Dt 12, тоже является вектором, причем коллинеарным вектору перемещения.
Очевидно, что если мы будем уменьшать величину интервала Dt 2 (приближая t 2 к t1), то соответственно будет уменьшаться и длина вектора Dr12, то есть величина перемещения. Предел отношения перемещения Dr 12 к интервалу Dt 2, когда последний стремится к нулю, называют производной вектора r (t) по времени t:
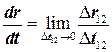 (2.4)
(2.4)
Этот вектор направлен по касательной к траектории материальной точки в точке t1. Мгновенной скоростью материальной точки называется предел отношения приращения перемещения к приращению времени, или

Это, очевидно, вектор, направленный по касательной к траектории в точке, соответствующей моменту времени t, с компонентами:

 (2.5)
(2.5)

Вектор скорости частицы υ(t) так же, как и радиус-вектор, является функцией времени t. Аналогичным образом можно определить вектор, характеризующий скорость изменения скорости частицы и называемый ускорением:
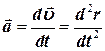 (2.6)
(2.6)
Если величина и направление этого вектора не изменяются со временем, то есть, если а = const то такое движение называется равноускоренным (равнопеременным).
Для равноускоренного движения скорость материальной точки υ(t) и ее радиус-вектор r(t) изменяются со временем по закону
υ(t)=υ0+at
r(t)=r0+υ0(t)+  at2, (2.7)
at2, (2.7)
где υ ( 0 ) и r(0)— соответственно скорость и радиус-вектор материальной точки в начальный момент времени t0 (проверка дифференцированием). Траекторией точки при равноускоренном движении является, как известно, парабола. Частным случаем равноускоренного движения является движение с ускорением, равным нулю. Такое движение называется равномерным. Очевидно, что оно происходит по прямой.
Рассмотрим теперь вопрос, как найти путь, проходимый материальной точкой при ее движении. Рассмотрим произвольного вида траекторию, по которой движется материальная точка. Пусть в момент времени t1 материальная точка занимала положение на траектории, характеризуемое радиус-вектором r1, а в момент времени t2 — радиус-вектором r2, рис. 2.1. Спрашивается, какой путь прошла материальная точка между этими двумя положениями. Перемещение материальной точки определяется вектором Dr, но длина этого вектора, очевидно, не определяет пройденный материальной точкой путь, за исключением того случая, когда траектория материальной точки между двумя положениями представляет собой прямую линию. Это подсказывает способ нахождения пути при криволинейном движении. Для этого разобьем временной интервал t2–t1 на много одинаковых интервалов очень малой продолжительности D t, так что в каждом таком малом интервале движение практически прямолинейное. Число таких интервалов равно
п = 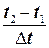 .
.
Изобразим векторы перемещения материальной точки в каждом из этих интервалов времени. Очевидно, что при достаточно малом D t, пройденный путь S может быть аппроксимирован суммой длин этих векторов:
 (2.8)
(2.8)
По мере стремления D t к нулю это приближение становится все лучше и лучше и в конце концов при бесконечном п обращается в точное равенство.
Разделим и помножим каждое слагаемое в этой сумме на D t:
 . (2.9)
. (2.9)
Очевидно, можно поменять местами операции суммирования и предельного перехода (предел суммы ранен сумме пределов) и вспомнить, что предел равен скорости частицы υ в i- том интервале. Тогда путь может быть представлен в виде суммы бесконечного числа бесконечно малых слагаемых:
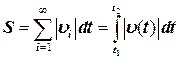 .
.
Таким образом, мы пришли к такому результату, что:
путь, пройденный частицей в интервале ее движения от t1 до t2. равен определенному интегралу по времени в этих пределах от модуля скорости частицы.
Лекция 3







 Поступательное движение – это движение, при котором все точки тела движутся по параллельным траекториям.
Поступательное движение – это движение, при котором все точки тела движутся по параллельным траекториям. Рассмотрим теперь движение материальной точки, траектория которой изображена на рис, 2.1, и определим такие важные для дальнейшего понятия, как скорость материальной точки υ и ускорение а.
Рассмотрим теперь движение материальной точки, траектория которой изображена на рис, 2.1, и определим такие важные для дальнейшего понятия, как скорость материальной точки υ и ускорение а.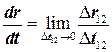 (2.4)
(2.4)

 (2.5)
(2.5)
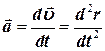 (2.6)
(2.6) at2, (2.7)
at2, (2.7)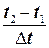 .
. (2.8)
(2.8) . (2.9)
. (2.9)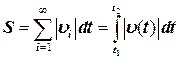 .
.


