Д.Бернулли вывел соотношение для установившегося движения идеальной несжимаемой жидкости, носящее название уравнения Бернулли.
 Выделим в трубке тока (см. рис. 9.2) элемент, ограниченный плоскими сечениями S1 и S2.
Выделим в трубке тока (см. рис. 9.2) элемент, ограниченный плоскими сечениями S1 и S2.
Жидкость втекает слева в сечение 1 площадью S 1, находящееся на высоте z 1 над уровнем земли. Скорость втекающих частиц жидкости перпендикулярна к сечению трубы и равна v 1, давление в жидкости при входе в трубу равно p 1.
Через сечение 2площадью S2, находящееся на высоте h 2 над уровнем земли, жидкость вытекает из трубы со скоростью v 2 давление в жидкости на выходе из трубы равно р 2. Жидкость течет через трубу под действием разности приложенных извне давлений p 1 – р 2 или разности уровней h 1 – h 2, приводящей к гидростатическому давлению соответствующего столба жидкости, или того и другого вместе.
За бесконечно малый промежуток времени d t через сечение S 1 втекает масса жидкости d m, заполняющая цилиндрик с площадью основания S 1и высотой v 1d t (заштрихованный на рисунке). За тот же промежуток времени через сечение 2 вытечет такая же масса жидкости d m, заполнявшая цилиндрик с площадью основания S 2 и высотой v 2d t (также заштрихованный на рисунке). Значение d m можно найти, умножив величину каждого из этих элементарных объемов на плотность жидкости ρ. Тогда получим:
d m = ρ S 1 υ 1 d t = ρ S 2 υ 2 d t.
При перемещении изменяется кинетическая и потенциальная энергии выделенного элемента. По закону сохранения энергии величина этого изменения определяется работой сил давления f1 = p1S1 и f2 = p2S2, которые действуют на плоскости S1 и S2.
Полная сила давления, действующая на левое сечение, равна p 1 S 1. Эта сила переместила массу жидкости d m на расстояние υ 1d t. За то же время в правом сечении такаяже масса жидкости d m переместилась на расстояние υ 2d t и совершила работу против силы давления p 2 S 2.
Полная работа А сил давления при таком перемещении равна
А = p 1 S 1 υ 1 d t – p 2 S 2 υ 2 d t
Эта работа затрачена на увеличение кинетической энергии элемента жидкости с массой d m, скорость которого изменилась от v 1на входе до v2 на выходе, и на изменение потенциальной энергии этого элемента в поле тяжести при переходе с уровня h 1на уровень h 2.
Пусть плотность жидкости в сечении S1 равна r1, а в сечении S2 - r2. Масса отрезка между сечениями S1 и S`1 равна m1 = r1υ1S1dt, тогда как масса между S2 и S 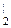 равна m2 = r2υ2S
равна m2 = r2υ2S 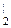 dt; поэтому кинетическая и потенциальная энергии массы m1 равны:
dt; поэтому кинетическая и потенциальная энергии массы m1 равны:
 =
= 
 . (9.8)
. (9.8)
Аналогично для массы m2:
 =
= 
 (9.9)
(9.9)
На основании закона сохранения механической энергии можно записать:
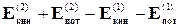 =
=  . (9.10)
. (9.10)
Работа силы f2 взята со знаком минус потому, что направление силы и направление перемещения противоположны друг другу.
Подставляя в уравнение (9.10) значения кинетических и потенциальных энергий (9.8) и (9.9), получаем:



 =
=  , (9.11)
, (9.11)
откуда после сокращения на величину dt (с учетом того, что v1S1 =v2 S2) следует:


 =
= 

 , (9.12)
, (9.12)
или в общем виде:

 + р = const. (9.13)
+ р = const. (9.13)
Выражения (9.12) и (9.13) представляют различные формы записи уравнения Бернулли, имеющего ряд важных следствий практического характера.
Уравнение Бернулли выражает закон сохранения энергии при установившемся движении несжимаемой идеальной жидкости. Это уравнение справедливо для любого движущегося объема жидкости вдоль траектории его движения, называемой линией тока.
Если движение жидкости или газа происходит на постоянной высоте, то уравнение (9.13) упрощается:
 р = const, или
р = const, или 
 =
= 
 . (9.14)
. (9.14)
Из этого уравнения следует, что давление внутри трубки тока зависит от скорости: там, где скорость меньше, давление больше, при увеличении скорости потока давление в нем уменьшается. Это утверждение называют принципом Бернулли.
Величина  представляет собой удельную кинетическую энергию, т.е. кинетическую энергию единицы объема движущейся жидкости. Величина
представляет собой удельную кинетическую энергию, т.е. кинетическую энергию единицы объема движущейся жидкости. Величина  есть удельная потенциальная энергия в поле тяжести. Соответственно этому, величина р представляет собой удельную потенциальную энергию сил давления в жидкости.
есть удельная потенциальная энергия в поле тяжести. Соответственно этому, величина р представляет собой удельную потенциальную энергию сил давления в жидкости.
При движении элементарного объема жидкости происходит непрерывный переход его энергии из одной формы в другую, но полная энергия этого объема остается неизменной.
Так как все члены уравнения Бернулли имеют размерность давления, то это уравнение часто формулируют иначе. Давление р называют статическим напором, величину  – гидравлическим напором, а величину
– гидравлическим напором, а величину  – скоростным, или динамическим, напором. Тогда следует, что полный напор в движущейся жидкости, складывающийся из статического, гидравлического и скоростного напоров, остается постоянным.
– скоростным, или динамическим, напором. Тогда следует, что полный напор в движущейся жидкости, складывающийся из статического, гидравлического и скоростного напоров, остается постоянным.
Работами Д. Бернулли и его современника Эйлера были заложены основы науки о движении жидкостей, выросшей в настоящее время в самостоятельную науку – гидродинамику. Широкое практическое применение гидродинамика получила в конце XIX и начале XX веков в результате работ Н.Е.Жуковского и С.А.Чаплыгина. Ими была создана также новая наука – аэродинамика – учение о законах движения газов и теория полета. Жуковскому первому удалось объяснить механизм подъемной силы, создаваемой крылом аэроплана при движении. На рисунке изображен разрез примерного профиля крыла. Пунктиром показаны линии тока встречного течения воздуха. Как видно из рисунка, над верхней частью крыла происходит сгущение этих линий и увеличение относительной скорости воздушного потока. Согласно уравнению Бернулли давление в потоке над крылом станет меньше, чем под крылом, и за счет этой разности давлений возникает подъемная сила F, удерживающая летящий самолет в воздухе.
Нечто похожее наблюдается при обтекании неподвижной крыши потоками воздуха при ураганных ветрах: внутри дома воздух неподвижен, тогда как на наружной части крыши его скорость достигает 40 М/c. В этом случае давление воздуха изнутри, которое больше наружного, как бы поднимает крышу вверх. При больших скоростях потока прочности конструкции скрепляющих балок может оказаться недостаточно; в этом случае ветер снесет крышу с дома.
Еще одним примером проявления принципа Бернулли служит пульверизатор, который схематически изображен на рис. 9.4. Если пробка сосуда, содержащего жидкость, плотно прижата, то при сжимании резиновой груши образуется ток воздуха, давление в потоке уменьшается, и под давлением воздуха, находящегося внутри сосуда, жидкость устремляется вверх. Оконечность горизонтальной трубки сужена в виде сопла, что способствует еще большему увеличению скорости потока воздуха, который увлекает за собой капли поднимающейся жидкости. Аналогом пульверизатора является пульт для разбрызгивания краски или побелки. В домашних условиях обычно используется упрощенный вариант этого устройства, где поток воздуха создается обыкновенным пылесосом. Для этого достаточно всасывающий шланг присоединить к выходному отверстию пылесоса.
Лекция 10





 Выделим в трубке тока (см. рис. 9.2) элемент, ограниченный плоскими сечениями S1 и S2.
Выделим в трубке тока (см. рис. 9.2) элемент, ограниченный плоскими сечениями S1 и S2.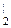 равна m2 = r2υ2S
равна m2 = r2υ2S  =
= 
 . (9.8)
. (9.8) =
= 
 (9.9)
(9.9)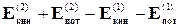 =
=  . (9.10)
. (9.10)


 =
= 

 =
= 

 , (9.12)
, (9.12)
 + р = const. (9.13)
+ р = const. (9.13)
 представляет собой удельную кинетическую энергию, т.е. кинетическую энергию единицы объема движущейся жидкости. Величина
представляет собой удельную кинетическую энергию, т.е. кинетическую энергию единицы объема движущейся жидкости. Величина  есть удельная потенциальная энергия в поле тяжести. Соответственно этому, величина р представляет собой удельную потенциальную энергию сил давления в жидкости.
есть удельная потенциальная энергия в поле тяжести. Соответственно этому, величина р представляет собой удельную потенциальную энергию сил давления в жидкости.


































