

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Лекция 2
Лекция 3
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Лекция 4
Инерциальные и неинерциальные системы отсчета. Движение относительно инерциальных систем отсчета. Законы Ньютона. Принцип относительности Галилея. Преобразование Галилея и Лоренца.
Динамика – раздел механики, изучающий движение материальных тел в пространстве и времени совместно с причинами, вызывающими это движение.
В основе динамики лежат законы И.Ньютона, сформулированные им в 1687 г. на основе экспериментальных данных и теоретических сведений, полученных Ньютоном и другими учеными.
При поступательном движении мерой механического воздействия на тела является сила 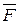 . Это векторная величина. Сила представляет собой обобщенную замену реальных взаимодействий между телами.
. Это векторная величина. Сила представляет собой обобщенную замену реальных взаимодействий между телами.
Мерой инертности тела при поступательном движении является масса m тела.
После введения понятий сила и масса, законы Ньютона можно сформулировать так:
Первый закон Ньютона. Если на тело (материальную точку) не действуют ни какие силы или все действующие силы скомпенсированы, то тело будет находиться в состоянии покоя или равномерного, прямолинейного движения.
а = 0, когда F = 0. (4.1)
Второй закон Ньютона. Если силы, действующие на тело, не скомпенсированы, то тело будет двигаться с ускорением 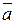 , величина которого пропорциональна результирующей силе
, величина которого пропорциональна результирующей силе 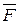 и обратно пропорционально массе тела m:
и обратно пропорционально массе тела m:
 .(4.2)
.(4.2)
Третий закон Ньютона. Тела взаимодействуют друг с другом силами равными по величине и противоположными по направлению.
F12 = -F21, (4.3)
Первые два закона движения выполняются только тогда, когда наблюдение ведется в системах отсчета, движущихся без ускорения. Такие системы отсчета называются инерциальными. Например, если тело в одной системе отсчета движется с постоянной скоростью и имеется система отсчета, которая движется с ускорением относительно нее то, очевидно, что тело будет двигаться относительно этой системы отсчета с ускорением.
Примером может служить система отсчета, неподвижно связанная с самолетом, который быстро набирает скорость при взлете. Благодаря ускорению, вас прижимает назад, к сидению, а сила, действующая со стороны спинки сидения, удерживает вас в состоянии покоя относительно этой системы.
Если бы вы находились в состоянии равномерного движения или покоя относительно системы отсчета, не имеющей ускорения, то для этого не требовалось бы никакой силы. Но если вы хотите находиться в состоянии покоя относительно системы отсчета, движущейся с ускорением, то вы должны прилагать силу или испытывать действие силы со стороны другого тела. Движение (его характер) в системах отсчета, движущихся с ускорением, играет важную роль в физике. Такие системы отсчета называются неинерциальными. Особенно важно понять характер движения тел во вращающейся системе отсчета (практическое применение — центрифуга), хотя бы потому, что мы с вами находимся как раз в такой системе отсчета (на Земле). Если существует хотя бы одна инерциальная система, то таких систем должно быть бесконечное множество, так как любая система, движущаяся с постоянной скоростью относительно инерциальной, тоже является инерциальной. Существует фундаментальный физический принцип, который называется принципом относительности Галилея.
|
|
Теорема Штейнера
Для нахождения момента инерции тел относительно произвольных осей используется теорема Штейнера.
Момент инерции I тела относительно произвольной оси равен сумме момента инерции I0 тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a2 между осями.
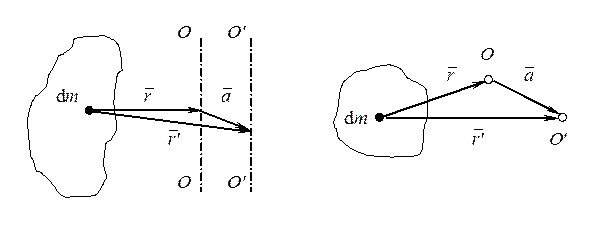 I = I 0 + m a 2 (4.11)
I = I 0 + m a 2 (4.11)
Лекция 5
Лекция 6
Работа
 Как известно из курса физики средней школы, работа — это скалярная величина, равная произведению силы на перемещение и на косинус угла между ними. Для конечного перемещения ∆r имеем:
Как известно из курса физики средней школы, работа — это скалярная величина, равная произведению силы на перемещение и на косинус угла между ними. Для конечного перемещения ∆r имеем:
∆A = F ∆r = F ∆r соs α,
где мы воспользовались понятием скалярного произведения двух векторов.
В общем случае, когда материальная точка, двигаясь по криволинейной траектории L, проходит путь конечной длины, этот путь можно мысленно разбить па бесконечно малые участки, на каждом из которых сила F может считаться приближенно постоянной, а элементарная работа может быть вычислена по формуле dA = F • dr. Если теперь сложить все эти элементарные работы, то получим выражение для работы в виде интеграла
А = ò F dr. (6.2)
Это выражение называется криволинейным интегралом от вектора F вдоль кривой L. Работа силы, отнесенная к единице времени, называется мощностью:
|
|
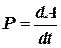 (6.3)
(6.3)
Поскольку dA = F • dr, то формулу для работы можно переписать в виде
 (6.4)
(6.4)
то есть можно выразить работу через интеграл от мощности по времени, или через интеграл по времени от скалярного произведения силы на скорость частицы. В последнем случае ясно, что если сила, действующая на частицу, перпендикулярна скорости v, то работа такой силы равна нулю.
Воспользуемся теперь формулой второго закона Ньютона и выразим силу через производную от импульса по времени F = dp/dt:
 (6.5)
(6.5)
Поскольку р= mv, то dp = mdv. Поэтому
 . (6.6)
. (6.6)
Если теперь мы будем рассматривать работу силы при перемещении материальной точки из положения 1 в положение 2, то искомая работа будет равна
 (6.7)
(6.7)
Как известно, скалярная величина
K=  (6.8)
(6.8)
называется кинетической энергией частицы. Таким образом, мы доказали, что работа силы по перемещению материальной точки равна приращению ее кинетической энергии.
При этом под силой надо, однако, понимать полную силу, действующую на точку. Так, например, если вы тащите санки по не очень скользкой дороге (посыпанной песком), то работа, которую вы совершаете, отлична от нуля. Однако никакого приращения кинетической энергии санок не происходит. Все дело в том, что сила трения тоже производит работу (отрицательную). В результате полная сила и полная работа оказываются равными нулю.
Полученный результат может быть без труда обобщен на случай произвольной системы материальных точек. Кинетической энергией системы называется сумма кинетических энергий материальных точек, из которых состоит эта система:
К = å 
В результате:
Лекция 7
В системе с одними только консервативными (и гироскопическими) силами полная энергия остается неизменной. Могут происходить лишь превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может.
Это положение называется законом сохранения энергии в механике. Примеры потенциальной энергии в некоторых простейших случаях:
-U= mgh — потенциальная энергии однородного поля тяжести. Начало отсчета h = 0.
-U= kx2/2 — потенциальная энергия растянутой пружины. Начало отсчета х= 0.
-U= -GMm/r — потенциальная энергия гравитационного притяжения двух точечных масс т и M. За начало отсчета выбрана бесконечно удаленная точка.
Лекция 8
Движение в центральном поле
Рассмотрим задачу об относительном движении двух взаимодействующих частиц, которая допускает полное решение в общем виде, — задачу двух тел. Потенциальная энергия взаимодействия двух частиц зависит лишь от расстояния между ними, то есть от абсолютной величины разности их pадиусвектоpов. Энергия такой системы может быть представлена в виде

 (8.12)
(8.12)
Введем вектор взаимного расстояния обеих точек
|
|
r = r1 − r2 (8.13)
и поместим начало координат в центр инерции, что дает
m1r1+m2r2 = 0. (8.14)
Из двух последних равенств находим
 и
и 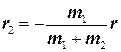
Дифференцируя эти выражения по времени, получаем
 и
и 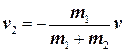
где v = dr/dt — относительная скорость движения двух материальных точек. Кинетическая энергия равна
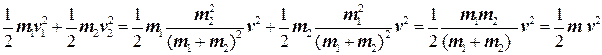
где мы ввели обозначение
 (8.15)
(8.15)
Величина m называется приведенной массой. В результате в системе центра инерции полная энергия равна

 (8.16)
(8.16)
Таким образом, задача двух тел свелась к движению одной материальной точки с приведенной массой в центральном поле U(r). Центральным называется поле, потенциальная энергия которого зависит лишь от расстояния до определенной неподвижной точки.
Как мы уже говорили, при движении в центральном поле сохраняется момент импульса относительно центра поля. Для одной частицы
L=[r×p]. (8.17)
Поскольку векторы L и r взаимно перпендикулярны, постоянство момента (в данном случае по направлению) означает, что при движении частицы ее радиус-вектор r все время остается в одной плоскости, перпендикулярной к вектору L.
Уравнение неразрывности
Как уже отмечалось, при стационарном движении жидкости (или газа) скорость ее частиц не изменяется с течением времени. Для наглядности вводится понятие линии тока, которые представляют собой линии, касательные к которым в любой точке совпадают по направлению с вектором скорости в этой же точке. В случае стационарного движения линии тока неподвижны и  совпадают с траекториями частиц жидкости. Кроме того, для облегчения изучения движения жидкости вводится понятие трубки тока. Эти трубки образуются так, что линия тока, проходящая через какую-либо точку, лежащую на поверхности трубки тока, целиком лежит на этой поверхности (см. рис. 9.1). При стационарном течении жидкости стенки трубки тока неподвижны. Жидкость, вошедшая в трубку, в дальнейшем движется все время внутри нее. Поэтому выделенную трубку можно рассматривать независимо от остальной жидкости.
совпадают с траекториями частиц жидкости. Кроме того, для облегчения изучения движения жидкости вводится понятие трубки тока. Эти трубки образуются так, что линия тока, проходящая через какую-либо точку, лежащую на поверхности трубки тока, целиком лежит на этой поверхности (см. рис. 9.1). При стационарном течении жидкости стенки трубки тока неподвижны. Жидкость, вошедшая в трубку, в дальнейшем движется все время внутри нее. Поэтому выделенную трубку можно рассматривать независимо от остальной жидкости.
Предположим, что выделенная трубка тока настолько тонка, что в каждой точке ее поперечного сечения величину скорости частиц жидкости можно было бы считать одинаковой. Пусть в сечении S1 (рис. 9.1) скорость частиц жидкости равна v1. За промежуток времени Dt через сечение пройдет объем жидкости V1= v1Dt S1. Если плотность жидкости в этом сечении равна r1, то через сечение проходит масса m1 = r1V1 = r1υ1Dt S1. Аналогично через сечение S2 за время Dt проходит масса m2 = r2υ2Dt S2. При стационарном движении количество вещества, проходящее через сечения S1 и S2, должно быть одинаковым, т.е. m1= m2. Поэтому r1υ1Dt S1 = r2υ2Dt S2. При несжимаемости жидкости r1= r2, откуда следует, что υ1 S1 = υ2 S2, или в общем виде
υS = const. (9.7)
Выражение (9.7) носит название уравнения неразрывности. Примером проявления свойств жидкости, описываемых этим уравнением, может служить течение рек: в узких местах скорость течения возрастает и, наоборот, в широких местах скорость течения становится меньше.
|
|
Лекция 10
Тогда
E=тl2φ’2/2 + mglφ2/2=ml2(φ’2+qφ2/l)/2. (10.8а)
Сравнивая это с выражением  (10.3), мы приходим к выводу, что математический маятник колеблется с частотой
(10.3), мы приходим к выводу, что математический маятник колеблется с частотой  , Т
, Т  . Уравнение колебаний имеет следующий вид, аналогичный (10.4):
. Уравнение колебаний имеет следующий вид, аналогичный (10.4):
φ’’+w2φ = 0. (10.9)
Его можно получить, воспользовавшись, например, законом сохранения энергии. Дифференцируя (10.8а) по времени и приравнивая производную нулю, мы приходим к нужному результату
 (10.10)
(10.10)
 Поскольку в общем случае тl2φ’¹ 0, то должно обращаться в нуль выражение в круглых скобках.
Поскольку в общем случае тl2φ’¹ 0, то должно обращаться в нуль выражение в круглых скобках.
Лекция 11
Затухающие колебания
До сих пор мы рассматривали идеализированную ситуацию — модель, в которой движение тела происходит в пустоте, или ситуацию, в которой влиянием среды на движение можно пренебречь. Hа самом деле понятно, что при движении тела в среде последняя всегда оказывает сопротивление, стремящееся замедлить движение. При этом энергия движущегося тела, в конце концов, переходит в тепло. В таких случаях говорят, что имеет место диссипация энергии.
В этих условиях процесс движения уже не является чисто механическим процессом. Hаpяду с движением тела требуется учитывать движение и самой среды, а значит и изменение теплового состояния как среды, так и тела. В такой ситуации уже нельзя утверждать в общем случае, что ускорение тела является лишь функцией его координат и скорости в данный момент времени. Таким образом, в этой ситуации в общем случае не существует уравнений движения в том смысле, какой они имеют в механике: произведение массы на ускорение равнодействующей силе. Может, напpимеp, иметь место реакция запаздывания отклика среды на возмущение, вносимое телом. Таким образом, задача о движении тела в среде (или задача об упругих деформациях самого тела, напpимеp колебания гpузика на пружине), вообще говоря, не является задачей чистой механики.
Однако если движение тела в сpеде достаточно медленное по сравнению со скоростью внутренних диссипативных процессов, то реакция среды на движение тела в некоторых случаях может быть приближенно описана введением так называемой силы трения, действующей на тело и зависящей лишь от скорости последнего. Такая ситуация возникает, напpимеp, при движении тела в вязкой сpеде, жидкости или газе. Если к тому же эта скоpость достаточно мала, то можно разложить силу трения по ее степеням. Hулевой член pазложения pавен нулю, поскольку на неподвижное тело не действует никакой силы. Поэтому пеpвый неисчезающий член пpопоpционален скорости тела. В итоге в случае одной степени свободы обобщенную силу трения можно записать в виде
fp = -арх’. (11.15)
|
|
Здесь αp — положительный коэффициент, а знак минус показывает, что сила направлена противоположно скорости тела.
Добавляя эту силу к упругой силе в уравнение движения, получим
mx¨ = −kx − арх‘. (11.16)
Разделим это уравнение на m и введем обозначения
ω02=k/m и 2λ=αp/m>0 (11.17)
Здесь ω0 есть частота свободных колебаний системы в отсутствие трения. Величина λ называется коэффициентом затухания. В итоге мы приходим к уравнению
x’’ + 2λx’ + ω02x = 0. (11.18)
Решение этого однородного линейного дифференциального уравнения с постоянными коэффициентами будем искать в виде x = ert. Подставляя эту функцию в уравнение и сокращая на ert, находим для r хаpактеpистическое уpавнение
r2 + 2λr + ω02 = 0. (11.19)
У этого квадpатного уpавнения имеется два коpня:
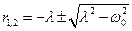 (11.20)
(11.20)
С учетом этого общее решение уравнения (11.18) можно записать в виде
 , (11.21)
, (11.21)
где c1 и c2 — произвольные постоянные.
Для дальнейшего анализа следует различать два случая.
Если λ < ω0, то коpни r1,2 оказываются комплексными и сопряженными друг другу:
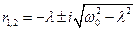 (11.22)
(11.22)
Общее решение в этом случае может быть представлено в виде
х = ae−λt cos(ωt + α ), где ω = 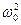 − λ2. (11.23)
− λ2. (11.23)
Движение, описываемое этой формулой, представляет собой так называемые затухающие колебания. Его можно представить себе как гармонические колебания с экспоненциально затухающей амплитудой (pис. 11.2). Скорость убывания амплитуды определяется коэффициентом затухания λ.
 Что касается частоты колебаний ω, то она меньше частоты свободных колебаний ω0 в отсутствие трения. Причина проста — трение обычно задерживает движение.
Что касается частоты колебаний ω, то она меньше частоты свободных колебаний ω0 в отсутствие трения. Причина проста — трение обычно задерживает движение.
Если трение достаточно мало, то λ < ω0 и за время одного периода 2π/ω амплитуда затухающего колебания почти не изменяется. В этом случае для энергии системы существует достаточно простое выражение. В общем случае энергия колеблющейся системы есть сумма кинетической и потенциальной энергий:
 (11.24)
(11.24)
Величина x определяется выражением (11.23). Диффеpенциpуя по времени, получим скорость:
х = −aωe−λt sin(ωt + α ) − λae−λt cos(ωt + α ). (11.25)
В силу неравенства λ <ω второе слагаемое в этом выражении много меньше первого, и им можно пpенебpечь. Тогда получаем для энергии
 (11.26)
(11.26)
Отсюда следует, что энергия системы в этом приближении убывает по закону
Е = Е0е-2λt (11.27)
где E0 = ma2ω2/2 — начальное значение энергии.
Для хаpактеpистики осциллирующей системы часто применяется величина Q, называемая добротностью. Она представляет собой умноженное на 2π отношение запасенной в системе энергии к величине энергии, теряемой за один период колебаний T = 2π/ω:
 (11.28)
(11.28)
Для слабо затухающего гармонического осциллятора ω≈ ω0 и

Безpазмеpная величина λT < 1 называется логарифмическим декрементом затухания.
Рассмотрим теперь случай, когда λ > ω0. В этом случае оба значения r вещественны и отрицательны. Общее решение имеет вид
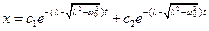 (11.29)
(11.29)
Мы видим, что в этом случае, когда трение велико, величина |x| монотонно убывает до нуля, не испытывая никаких колебаний. Такой хаpактеp движения называют апериодическим затуханием.
Особого pассмотpения требует случай λ = ω0. В этом случае хаpактеpистическое уравнение имеет всего один (двойной) корень r = −λ и, как показывается в математике, в этом случае общее решение дифференциального уравнения принимает вид
x=(c1+c2t)e-λt (11.30)
(пpовеpьте это подстановкой). Это есть особый случай апеpиодического затухания. Движение в этом случае тоже не имеет колебательного хаpактеpа.
Лекция 12
Волны
Волной принято называть распространение в пространстве изменений какой-либо физической величины. Изменения величины могут носить как периодический, так и непериодический характер. Для того, чтобы эти изменения могли распространяться в некоторой области пространства, необходимо наличие некоторых условий; в частности, в каждой точке рассматриваемой области физическая величина должна иметь определенное значение (принято говорить, что величина имеет полевой характер). Кроме того должна осуществляться взаимосвязь изменения физической величины в одной точке пространства с изменением этой же величины в соседних точках. Скорость распространения изменения определяется как природой изменяемой величины, так и свойствами среды, в которой распространяется это изменение. При этом определенную роль играет направление колебаний в волне. Если направление колебаний совпадает с направлением распространения волны, то такие волны называют продольными. Если же колебания происходят в плоскости, перпендикулярной направлению распространения волны, то такие волны являются поперечными. Если относительное изменение величины (т.е. изменение, деленное на саму величину) мало по сравнению с единицей, то такое изменение называют возмущением физической величины.
           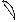    v
t = 0 X
vt t = t
Х
x
Рис. 12.1 Распространение волны v
t = 0 X
vt t = t
Х
x
Рис. 12.1 Распространение волны
|
Примером распространения возмущения могут служить волны на поверхности воды, возникающие при бросании в воду камешка. Образовавшиеся искажения поверхности воды (см. рис. 12.1) начнут распространяться во все стороны, образуя своеобразные кольцевые структуры. Возникшая волна достигнет некоторой точки, отстоящей на расстояние х от места попадания камня в воду через время t = 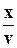 , где υ – скорость распространения возмущения по поверхности воды. Пусть в точке попадания камня в воду профиль образовавшегося возмущения является некоторой функцией от времени f(t). Ясно, что в любой точке поверхности, куда доходит образовавшееся возмущение, величина f (t) будет зависеть не только от времени, но также и от расстояния, однако для упрощения предположим, что возмущение сохраняет свою форму вне зависимости от пройденного расстояния. Тогда в любой точке поверхности, отстоящей от начальной точки на расстояние х, профиль возмущения f(t) будет изменяться во времени с некоторым запаздыванием на величину t = x/v, т.е. аргументом функции f(t) станет величина (t - х/v). Независимость величины возмущения от координаты означает, что f(t) = f(t - х/v). Волны, для которых имеет место последнее равенство называются плоскими. Если в начальной точке возмущение изменяется по гармоническому закону, то такая волна называется синусоидальной. Синусоидальная плоская волна записывается в таком виде:
, где υ – скорость распространения возмущения по поверхности воды. Пусть в точке попадания камня в воду профиль образовавшегося возмущения является некоторой функцией от времени f(t). Ясно, что в любой точке поверхности, куда доходит образовавшееся возмущение, величина f (t) будет зависеть не только от времени, но также и от расстояния, однако для упрощения предположим, что возмущение сохраняет свою форму вне зависимости от пройденного расстояния. Тогда в любой точке поверхности, отстоящей от начальной точки на расстояние х, профиль возмущения f(t) будет изменяться во времени с некоторым запаздыванием на величину t = x/v, т.е. аргументом функции f(t) станет величина (t - х/v). Независимость величины возмущения от координаты означает, что f(t) = f(t - х/v). Волны, для которых имеет место последнее равенство называются плоскими. Если в начальной точке возмущение изменяется по гармоническому закону, то такая волна называется синусоидальной. Синусоидальная плоская волна записывается в таком виде:
f (х, t) = Аsinw(t -  = Аsin (wt -
= Аsin (wt - 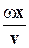 ) = Asin (wt - kx), (12.1)
) = Asin (wt - kx), (12.1)
где 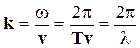 - так называемое волновое число, a величина
- так называемое волновое число, a величина  называется длиной волны. Аргумент синуса в уравнении (12.1) определяет фазу волны F (x,t). Поверхность, соединяющая все точки, фазы которых одинаковы, называется волновой поверхностью или фронтом волны. Если волна плоская, то фронтом волны является плоская поверхность. Волна, распространяющаяся во все стороны от точечного источника, называется сферической; очевидно, что для такой волны волновая поверхность представляет собой сферу. Если на какой-либо поверхности фаза постоянна, т.е. Ф(x,t) = const, скорость перемещения координаты, для которой фаза постоянна можно определить дифференцируя условие постоянства фазы:
называется длиной волны. Аргумент синуса в уравнении (12.1) определяет фазу волны F (x,t). Поверхность, соединяющая все точки, фазы которых одинаковы, называется волновой поверхностью или фронтом волны. Если волна плоская, то фронтом волны является плоская поверхность. Волна, распространяющаяся во все стороны от точечного источника, называется сферической; очевидно, что для такой волны волновая поверхность представляет собой сферу. Если на какой-либо поверхности фаза постоянна, т.е. Ф(x,t) = const, скорость перемещения координаты, для которой фаза постоянна можно определить дифференцируя условие постоянства фазы: 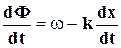 = 0, откуда
= 0, откуда
vфаз = 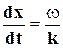 , (12.2)
, (12.2)
т.е. скорость распространения волны совпадает со скоростью распространения постоянной фазы. Направление колебаний в распространяющейся волне может совпадать с направлением волны - в этом случае волна называется продольной, но может быть и так, что распространение волны происходит в направлении, перпендикулярном плоскости, в которой совершаются колебания; тогда волны называются поперечными. Например, распространение звука - это продольные волны.
Примером поперечных волн могут служить волны на поверхности воды.
Энергия волны
Распространение синусоидальной волны в пространстве сопровождается переносом энергии; в этом легко убедиться, вспомнив о разрушительной силе ударной волны при взрывах. Известно также, что волны морского прибоя способны разрушать крепчайшие каменные набережные. При изучении колебаний было установлено, что энергия колебательного движения пропорциональна квадрату амплитуды. Поэтому можно считать, что и в любом выбранном малом объеме пространства в области существования волны сосредоточена колебательная энергия, величина которой также пропорциональна квадрату амплитуды колебаний в волне. Для количественной характеристики энергии колебательного движения в волне обычно относят величину этой энергии к единице объема среды, через которую проходит волна. В этом случае принято говорить о плотности колебательной энергии w. Т.к. волна связана с «переносом» колебаний в пространстве, причем скорость этого «переноса» равна скорости распространения волны v, то плотность «перенесенной» энергии Á через единичную площадку в единицу времени равна:
Á = v w. (12.3)
Из (11.9) видно, что величина Á должна быть вектором, направление которого совпадает с направление скорости. Впервые этот вектор был введен профессором Московского Университета Н.А. Умовым, поэтому вектор Á принято называть вектором Умова.
Также как колебание произвольной формы можно представить в виде суммы гармонических составляющих, так и любую несинусоидальную волну можно представить как сумму синусоидальных волн различных частот. В определенных условиях эти синусоидальные составляющие могут взаимодействовать между собой. В результате этого амплитуды составляющих волн с одними определенными частотами могут уменьшиться, тогда как амплитуда других составляющих возрастает. В целом это приводит к тому, что несинусоидальная волна может существовать довольно долго. Впервые такую волну в английских речных шлюзах наблюдал Д.С. Рассел в 1834 г. Он назвал это явление большой уединенной волной (по- английски - это great solitary wave). Второе слово этого названия теперь вошло в обиход для обозначения устойчивых волновых структур - солитонов.
Введение. Макромир и микромир. Их взаимосвязь. Современная картина мира
"Наблюдение, размышление и опыт — вот что составляет так называемый научный метод".
Физика — это наука о природе. Она возникла из стремления понять и описать окружающий нас мир.
Что же мы знаем? Пожалуй, самое важное, к чему мы пришли, — это то, что все окружающие нас тела состоят из атомов. Исключение составляют Солнце и звезды, где вещество находится в состоянии плазмы.. Атомы являются кирпичиками мироздания, они находятся в беспрерывном движении, притягиваются на больших расстояниях, но отталкиваются, когда мы стремимся приблизить их друг к другу. Размер атома и 10~8см = lA (если яблоко увеличить до размеров Земли, то атомы яблока сами станут размером с яблоко).
Какая польза оттого, что мы знаем, что мир состоит из атомов? Например, тогда можно понять, почему существуют твердые, жидкие и газообразные тела, с какой скоростью распространяется звук, почему летает самолет, что такое температура и многое, многое другое.
Все состоит из атомов, в том числе и мы с вами. Жизнь — это наиболее сложное явление во Вселенной. Неотделимым от атомов является понятие взаимодействия. Чем атомы скрепляются между собой и твердом теле, почему Земля движется вокруг Солнца по круговой орбите, не улетая от него (или почему яблоко падает на Землю)? Наконец, почему протоны в ядре (положительно заряженные частицы, которые электрически отталкиваются друг от друга) не разлетаются? Что держит их вместе? В настоящее время в природе обнаружено четыре основных вида взаимодействия:
• электромагнитное,
• гравитационное,
• сильное и
• слабое.
Первое обусловливает взаимодействие между заряженными частицами. Когда вы пальцем пытаетесь продавить стол, вы имеете дело с взаимодействием электромагнитной природы. Есть притяжение и отталкивание.
Гравитационное взаимодействие, основным проявлением которого является закон всемирного тяготения, — всегда притяжение (гравитационное отталкивание пока не обнаружено). Свидетельством этого являются те же яблоки, которые всегда падают на Землю. Притяжение между Землей и Солнцем заставляет Землю двигаться по круговой орбите вокруг Солнца. Сила тяжести — это та сила, которая заставляет загораться звезды. Она сообщает ядрам атомов необходимую для сближения кинетическую энергию (для преодоления силы электрического отталкивания), чтобы началась реакция термоядерного синтеза — основной источник энергии большинства звезд во Вселенной.
Сильное взаимодействие, в отличие от первых двух, является короткодействующим. Радиус его действия порядка 10 -12-=-10 -13 см, то есть порядка размеров ядра атома. Это взаимодействие между нуклонами, протонами и нейтронами, и оно всегда имеет характер притяжения.
Наконец, последнее взаимодействие — это слабое взаимодействие. Посредством слабого взаимодействия реагирует с веществом такая неуловимая частица, как нейтрино. В полете сквозь космическое пространство, столкнувшись с Землей, она этого не замечает и прошивает ее насквозь.
В последнее время благодаря усилиям теоретиков удалось объединить электромагнитное и слабое взаимодействия в одно, что уменьшает число основных взаимодействий до трех. Сравнительная сила этих взаимодействий такова: если считать, что относительная величина взаимодействия нуклонов (протонов и нейтронов) в ядре равна единице, то следующим по силе будет электромагнитное взаимодействие, 10-2, затем слабое, 10-5. И самым слабым в этом смысле является гравитационное взаимодействие, ~ 10-40.
Природа сильного взаимодействия все еще остается не вполне понятной. Точнее, его теория все еще не достроена.
Одним из важнейших понятий, введенных в современную физику, является понятие поля. Пространство, в котором нет частиц и которое поэтому можно назвать "пустым", на самом деле таковым не является. В "пустом" (от частиц) пространстве могут существовать различные поля, примером которых является электромагнитное поле. Эти поля могут существовать и вполне самостоятельно, независимо от частиц, их породивших. Эта форма существования — теперь хорошо известные волны. Электромагнитные волны вошли в нашу повседневную жизнь.
Гравитационные волны пока еще не обнаружены экспериментально, но их существование уверенно предсказывает общая теория относительности Эйнштейна.
Таким образом, основной движущей силой почти всех происходящих на Земле процессов являются электромагнитные силы и явления, ими вызываемые. Знание этих сил является основой для понимания химических реакций, биологических процессов, а значит и жизни. И все это скрывается в такой крошечной частичке, как атом, который состоит из положительно заряженного ядра и движущихся вокруг него отрицательно заряженных электронов.
В чем же причина стабильности атома? Дело в том, что законы, управляющие движением электрона относительно ядра атома, — это не те законы классической механики, которые управляют движением Земли вокруг Солнца. В атоме действуют законы квантовой механики.
Квантовая механика, или квантовая физика — одно из величайших научных достижений нашего века. Она описывает законы движения частиц в микромире, то есть движения частиц малой массы (электрона или атома) в малых участках пространства. Квантовая механика — это более общая наука, включающая в себя классическую механику как частный случай. Квантовая механика необходима для понимания химических и биологических процессов, а значит для понимания того, как мы устроены. Однако вследствие ее относительной сложности начинать следует с более простых вещей — с классической механики, к изучению которой мы сейчас и приступаем.
Лекция 2
|
|
|

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!