Разгон с постоянным ускорением – установившееся движение (с постоянной скоростью) – торможение с постоянным ускорением. Это – движение с четырьмя «мягкими» ударами (рис. П4).

Рис. П4. Законы изменения параметров движения при a (t) = const
Если заданы перемещение S, время разгона t р, время установившегося движения t у, время торможения t т, то:
перемещения при разгоне, движении с постоянной скоростью, торможении
 (П.13)
(П.13)
максимальная скорость
 (П.14)
(П.14)
ускорения при разгоне и торможении
 (П.15)
(П.15)
Если заданы перемещение S, ускорение a р = a т = a и время T перемещения на величину хода, то максимальная скорость:
 (П.16)
(П.16)
а если заданы S, V и a, то время перемещения
 (П.17)
(П.17)
Разгон – установившееся движение – торможение с ускорениями, изменяющимися по закону a (t) = a× sinw t. Это – безударное управляемое движение (рис. П5).
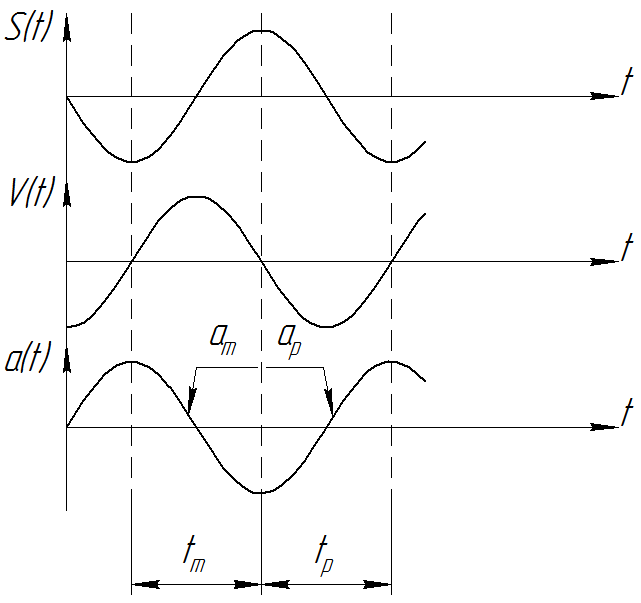
Рис. П5. Законы изменения параметров движения при a (t) = a× sinw t
текущее ускорение звена
на участке разгона
a (t) = a рsinw1 t, (П.18)
на участке торможения
a (t) = a тsinw2 t, (П.19)
где w1, w2 – круговые частоты на участках разгона и торможения;
w1 = 2p f 1 = p/ t р, w2 = 2p f 2 = p/ t т.
текущая скорость звена
на участке разгона
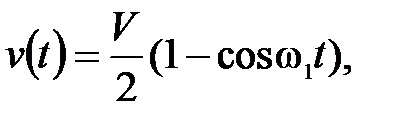 (П.20)
(П.20)
на участке торможения
 (П.21)
(П.21)
на участке установившегося движения
v (t) = V.
текущее перемещение звена S (t) = ò v (t) dt
на участке разгона
 (П.22)
(П.22)
на участке торможения
 (П.23)
(П.23)
на участке установившегося движения S (t) = Vt.
Если заданы перемещение S, время движения T, время разгона t р и время торможения t т, то
максимальная скорость
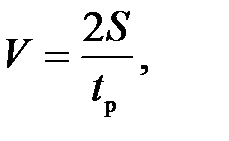 (П.24)
(П.24)
максимальное ускорение на участке разгона
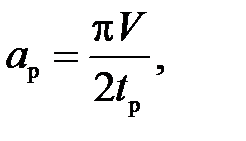 (П.25)
(П.25)
максимальное ускорение на участке торможения
 (П.26)
(П.26)
Движение точки звена по окружности
Перемещение точки по дуге радиуса R
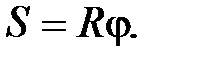 (П.27)
(П.27)
где j - угол дуги.
Угловая скорость
 (рад/с, 1/с), (П.28)
(рад/с, 1/с), (П.28)
где n - частота вращения или скорость вращения (об/мин, 1/мин).
Окружная скорость
V = w R (П.29)
Ускорение точки М (рис. П6)
 (П.30)
(П.30)

где an = w2 R – нормальное ускорение, a t = e R – тангенциальное ускорение.

Рис. П6. Ускорение точки звена при вращении
Скорость и ускорение точки звена при наличии относительного движения (рис. П7)
 (П.31)
(П.31)
где  - скорость и ускорение точки в переносном движении,
- скорость и ускорение точки в переносном движении,
 - скорость и ускорение точки в относительном движении,
- скорость и ускорение точки в относительном движении,
 - ускорение Кориолиса.
- ускорение Кориолиса.

Рис. П7. Переносное и относительное движение точки звена
СИЛА, МОМЕНТ СИЛЫ
Сложение сил
Равнодействующая сил  (рис. П8), приложенных в одной точке
(рис. П8), приложенных в одной точке
 (П.32)
(П.32)

Рис. П8. Сложение сил, приложенных в одной точке
Равнодействующая параллельных сил  (рис. П9)
(рис. П9)
 (П.33)
(П.33)

Рис. П9. Сложение параллельных сил
Момент силы F относительно оси Z (рис. П10)
 (П.34)
(П.34)
где F п – проекция силы  на плоскость П, перпендикулярную оси Z,
на плоскость П, перпендикулярную оси Z,
h – плечо силы.

Рис. П10. Момент силы относительно оси
Момент пары сил (рис. П11)
 (П.35)
(П.35)

Рис. П11. Момент пары сил
Параллельное смещение силы из точки А в точку В (рис. П12)

Рис. П12. Параллельное смещение силы
Эквивалентом силы FA является сила FB = FA и пара сил FA с плечом h.
Система уравнений равновесия звена
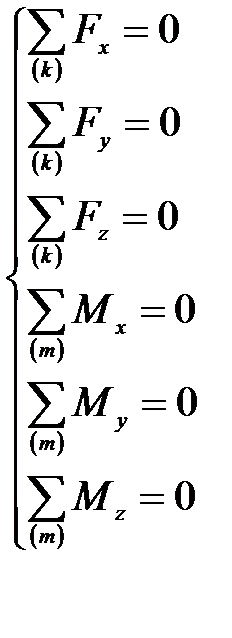 , (П.36)
, (П.36)
где Fx, Fy, Fz – проекции силы на оси координат;
Mx, My, Mz – моменты силы и моменты пары сил относительно осей координат;
k – число сил, действующих на звено;
m – число моментов сил и пар сил, действующих на звено.
Сила тяжести
 (П.37)
(П.37)
Тело массой 1 кг имеет вес G = 1×9,81 = 9,81 Н = 1 кгс.
Сила трения скольжения
 (П.38)
(П.38)
где f – коэффициент трения скольжения, который зависит от скорости скольжения V и изменяется от f max = f п до f min (рис. П13);
N – нормальное давление;
f п – коэффициент трения покоя.
При наличии смазки коэффициенты трения движения и покоя:
в паре сталь-сталь f = 0,1…0,2; f п = 0,2…0,3,
в паре сталь-бронза f = 0,1…0,15; f п = 0,15…0,2.
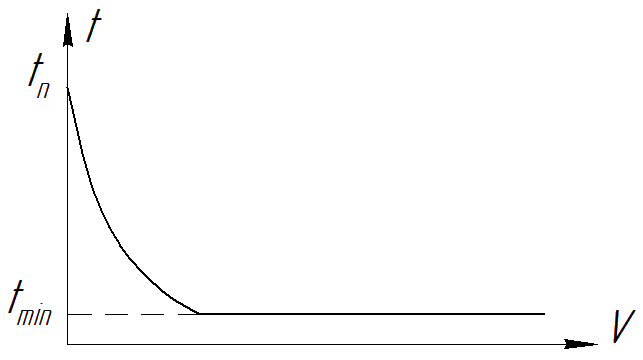
Рис. П13. Коэффициент трения скольжения
Момент трения в подшипнике скольжения
 (П.39)
(П.39)
где F р – радиальная нагрузка на подшипник;
d – диаметр подшипника.
Момент сопротивления при качении
 (П.40)
(П.40)
где k – коэффициент трения качения (плечо пары трения).
Для катка на плоской пластине
k» 1×10-5 м, если каток и пластина сделаны из закаленной стали,
k» 5×10-5 м, если каток и пластина сделаны из мягкой стали или чугуна.
Приведенная сила трения, которая действует на объект, движущийся на колесах (рис. П14)
 (П.41)
(П.41)
где f пр – приведенный коэффициент трения, который зависит от конструкции и качества узла колеса и от дороги.

Рис. П14. Объект на колесах
Момент трения в подшипнике качения
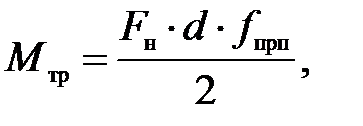 (П.42)
(П.42)
где  - нагрузка на подшипник;
- нагрузка на подшипник;
Fr и Fa – радиальная и осевая нагрузки на подшипник;
d – внутренний диаметр подшипника;
f прп – приведенный коэффициент трения в подшипнике, который учитывает все источники трения в подшипнике, f прп» const.
Для шариковых и роликовых подшипников f прп = 0,002…0,01.
Сила инерции в поступательном движении
 . (П.42)
. (П.42)
Момент сил инерции при вращении
 . (П.43)
. (П.43)
Движущая сила при поступательном движении
 (П.44)
(П.44)
где F тех – сила технологического сопротивления;
F тр – сила трения;
F и – сила инерции, F и = const при использовании принципа кинетостатики.
Движущий момент при вращении
 (П.45)
(П.45)
где М тех – момент технологического сопротивления;
М тр – момент сил трения;
М и – момент сил инерции.
Пример
Ползун П движется с ускорением и преодолевает технологическое сопротивление (рис. П15).
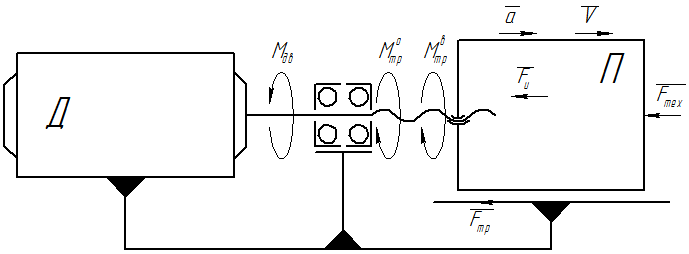
Рис. П15. Движущий момент при перемещении ползуна
Движущий момент на валу двигателя Д
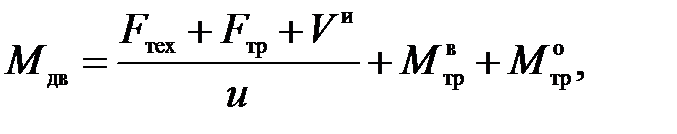
где F тех – технологическое усилие, действующее на ползун;
F тр – сила трения в опоре ползуна;
F и – сила инерции ползуна;
U – передаточное число винтовой передачи;
 – момент трения в винтовой передаче;
– момент трения в винтовой передаче;
 – момент трения в опоре винта.
– момент трения в опоре винта.
Гироскопический момент (рис. П16)
 (П.46)
(П.46)
где Jz – момент инерции звена, вращающегося вокруг оси своей симметрии;
w1 – скорость вращения звена;
w2 – скорость вращения оси симметрии;
q – угол между векторами  и
и  .
.
Уравнение движения при поступательном движении звена
 (П.47)
(П.47)
где m – масса звена;
 – ускорение центра масс;
– ускорение центра масс;
F – внешняя сила, действующая на звено;
N – число внешних сил.
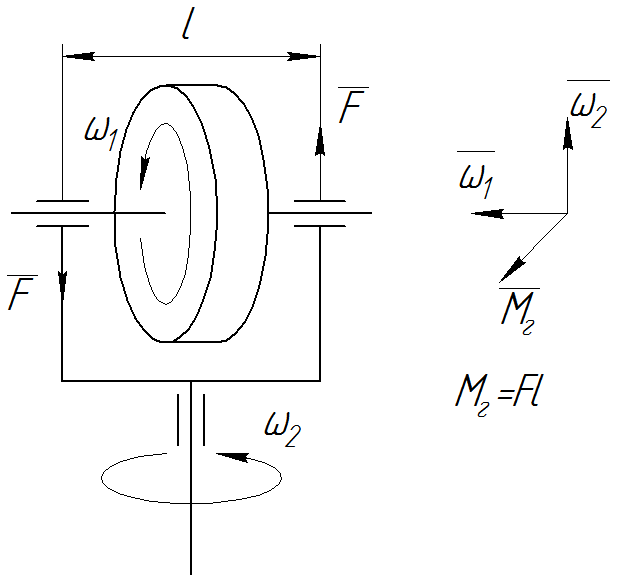
Рис. П16. Гироскопический момент
Уравнение движения при вращении звена вокруг оси
 (П.48)
(П.48)
где J – момент инерции звена;
 – угловое ускорение звена;
– угловое ускорение звена;
М – момент внешней силы, действующей на звено;
N – число моментов.
Кинетическая энергия звена, движущегося поступательно
 (П.49)
(П.49)
Кинетическая энергия вращающегося звена
 (П.50)
(П.50)
Потенциальная энергия (работа) при перемещении звена в поле сил тяжести
 (П.51)
(П.51)
где h 1 и h 2 - начальное и конечное положения звена по высоте подъема.
Потенциальная энергия сжатой (или растянутой) пружины
 (П.52)
(П.52)
где С - жесткость пружины;
l - деформация пружины.
Закон сохранения механической энергии
Т + П = const (П.53)
Уравнение Лагранжа 2-го рода
 (П.54)
(П.54)
где Т и П – кинетическая и потенциальная энергия системы;
qj – обобщенная координата, j = 1, 2, …;
 – обобщенная скорость;
– обобщенная скорость;
Qj – обобщенная сила.
Пример
Блок (рис. П17) весом G 0 радиуса r с массой, распределенной по ободу, приводится во вращение канатом, несущим грузы G 1 и G 2 > G 1. Найдем ускорение e блока.

Рис. П17. Блок с грузами
Выберем в качестве обобщенной координаты угол j. Тогда

где h 1, h 2 – начальные высоты грузов над горизонтальной плоскостью.

Мощность при поступательном движении
Р = FV (П.55)
Мощность при вращении
Р = М w (П.56)
Мощность двигателя
Р дв = Р из + Р пот, (П.57)
где Р из - мощность на исполнительном звене механизма;
Р пот - мощность потерь в передаче движения от двигателя к исполнительному звену.
Р дв = Р из/h (П.58)
где h - КПД передач движения, h = f (Р из).
Средняя мощность на участке траектории движения с координатой S 1 £ s £ S 2
 (П.59)
(П.59)
ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ
Упрощенная структура привода представлена на рис. П18.

Рис. П18. Структура привода
В качестве входа и выхода привода могут рассматриваться перемещение S, скорость V, ускорение a, сила F для поступательного движения или соответственно угол поворота j, угловая скорость w, угловое ускорение e, момент М – для вращательного движения.
Передаточное отношение механизма от двигателя (входа) к исполнительному звену (выходу)
 . (П.60)
. (П.60)
Отметим, что формула (П.60) соответствует «поступательному типу» входа и выхода. В случае «вращательного типа» в числителе и знаменателе должны использоваться соответствующие угловые характеристики. Например, при вращательном входе и поступательном выходе
 .
.
Передаточное отношение механизма колеса (рис. П19)

Рис. П19. Механизм колеса
1 – объект на колесах; 2 – колесо
Если колесо 2 ведущее (вход)
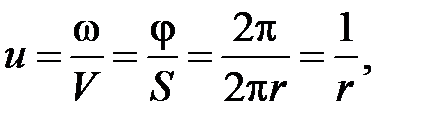
где r – радиус колеса.
Если объект 1 ведущий

Передаточное отношение механизма с зубчатой передачей (рис. П20)
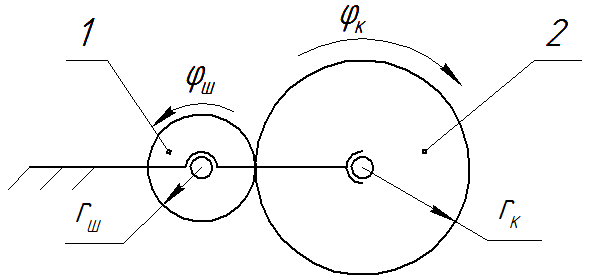
Рис. П20. Механизм с зубчатой передачей
1 – шестерня; 2 – колесо
Если шестерня ведущая

где z 1, z 2 – число зубьев на шестерне и колесе 8.
Передаточное отношение винтового механизма (рис. П21)

Рис. П21. Винтовой механизм
1 – ползун; 2 – направляющая; 3 – винт; 4 – гайка
Если винт ведущий

где t – шаг винта;
z – число заходов винта.
Передаточное отношение кривошипно-ползунного механизма (рис. П22)

Рис. П22. Кривошипно-ползунный механизм
1 – кривошип; 2 – шатун; 3 – ползун; 4 – направляющая
Если кривошип ведущий
 .
.
Если ползун ведущий
 .
.
Полное передаточное отношение механизма, включающего ряд последовательно соединенных механизмов с передаточными отношениями u 1, u 2 ,…, u n
 . (П.61)
. (П.61)
Пример.
Определим передаточное отношение для привода поворота платформы (рис. П23).

Рис. П23. Пневмопривод поворота платформы
1 – пневмоцилиндр; 2 – зубчатая рейка; 3, 4, 5 – зубчатые колеса; 6 – платформа
При перемещении штока пневмоцилиндра (двигателя) 1 на величину S платформа 6 поворачивается на угол j. Полное передаточное отношение

где u 1 – передаточное отношение рейка - колесо 3;
u 2 – передаточное отношение колесо 4 - колесо 5;
m – модуль в передаче рейка - колесо 3;
z 3, z 4, z 5 – числа зубьев колес 3, 4, 5.
Для схемы, представленной на рис. П18, имеем
· перемещение на двигателе
S вх (или jвх) = S вых× u (или jвых× u)
· скорость на двигателе
V вх (или wвх) = V вых× u (или wвых× u)
· ускорение на двигателе
a вх (или eвх) = a вых× u (или eвых× u)
· усилие на двигателе
F вх (или M вх) = F вых/ u (или M вых/ u).
| Тимофеев Александр Николаевич
Попов Аркадий Николаевич
Полищук Михаил Нусимович
|






 (П.13)
(П.13) (П.14)
(П.14) (П.15)
(П.15) (П.16)
(П.16) (П.17)
(П.17)
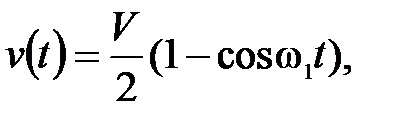 (П.20)
(П.20) (П.21)
(П.21) (П.22)
(П.22) (П.23)
(П.23)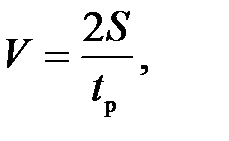 (П.24)
(П.24)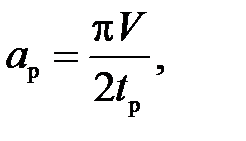 (П.25)
(П.25) (П.26)
(П.26)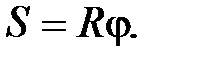 (П.27)
(П.27) (рад/с, 1/с), (П.28)
(рад/с, 1/с), (П.28) (П.30)
(П.30)

 (П.31)
(П.31) - скорость и ускорение точки в переносном движении,
- скорость и ускорение точки в переносном движении, - скорость и ускорение точки в относительном движении,
- скорость и ускорение точки в относительном движении, - ускорение Кориолиса.
- ускорение Кориолиса.
 (рис. П8), приложенных в одной точке
(рис. П8), приложенных в одной точке (П.32)
(П.32)
 (П.33)
(П.33)
 (П.34)
(П.34) на плоскость П, перпендикулярную оси Z,
на плоскость П, перпендикулярную оси Z,
 (П.35)
(П.35)

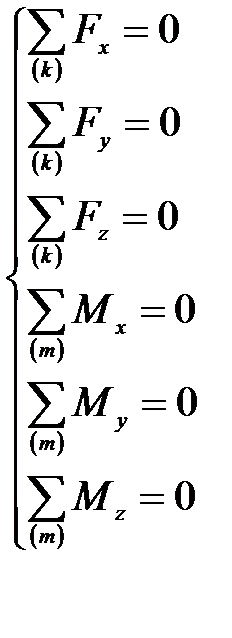 , (П.36)
, (П.36) (П.37)
(П.37) (П.38)
(П.38)
 (П.39)
(П.39) (П.40)
(П.40) (П.41)
(П.41)
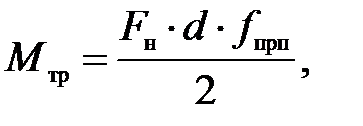 (П.42)
(П.42) - нагрузка на подшипник;
- нагрузка на подшипник; . (П.42)
. (П.42) . (П.43)
. (П.43) (П.44)
(П.44) (П.45)
(П.45)
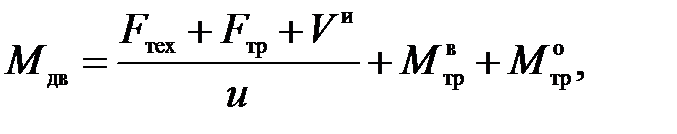
 – момент трения в винтовой передаче;
– момент трения в винтовой передаче; – момент трения в опоре винта.
– момент трения в опоре винта. (П.46)
(П.46) и
и  .
. (П.47)
(П.47) – ускорение центра масс;
– ускорение центра масс;
 (П.48)
(П.48) – угловое ускорение звена;
– угловое ускорение звена; (П.49)
(П.49) (П.50)
(П.50) (П.51)
(П.51) (П.52)
(П.52) (П.54)
(П.54) – обобщенная скорость;
– обобщенная скорость;


 (П.59)
(П.59)
 . (П.60)
. (П.60) .
.
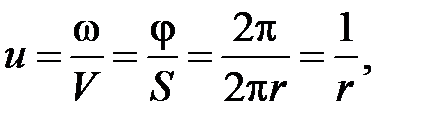






 .
. .
. . (П.61)
. (П.61)




