Пусть функция 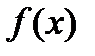 определена и непрерывна на
определена и непрерывна на 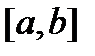 , дифференцирована в
, дифференцирована в  , за исключением конечного количества точек. По первой и второй теоремам Вейерштрасса она ограничена и достигает на этом сегменте своих точных верхней и нижней границ, которые являются ее наибольшим и наименьшим значениями на этом сегменте. Надо эти значения найти.
, за исключением конечного количества точек. По первой и второй теоремам Вейерштрасса она ограничена и достигает на этом сегменте своих точных верхней и нижней границ, которые являются ее наибольшим и наименьшим значениями на этом сегменте. Надо эти значения найти.
Допустим, что 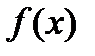 не имеет на
не имеет на 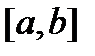 точек, где
точек, где  , или
, или 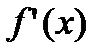 не существует. Это означает, что
не существует. Это означает, что 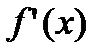 сохраняет свой знак везде на
сохраняет свой знак везде на 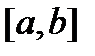 , а функция
, а функция 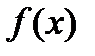 - строго монотонна на
- строго монотонна на 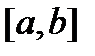 . Тогда наименьшее и наибольшее значения она будет принимать на концах сегмента
. Тогда наименьшее и наибольшее значения она будет принимать на концах сегмента 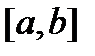 .
.
Если 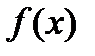 на сегменте
на сегменте 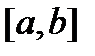 имеет конечное число точек
имеет конечное число точек 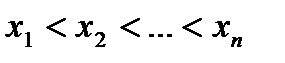 , где
, где 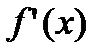 не существует или равняется нулю, то эти точки разбивают сегмент
не существует или равняется нулю, то эти точки разбивают сегмент 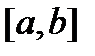 на частичные сегменты:
на частичные сегменты:  , в каждом из которых уже нет таких точек, где
, в каждом из которых уже нет таких точек, где  или
или 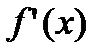 не существует, а потому
не существует, а потому 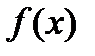 - строго монотонна на каждом из
- строго монотонна на каждом из  , а потому наименьшее и наибольшее значения она будет принимать на концах
, а потому наименьшее и наибольшее значения она будет принимать на концах  .
.
Таким образом, для того, чтобы найти наименьшее и наибольшее значения непрерывной на сегменте 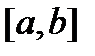 функции надо:
функции надо:
1. Найти производную функции на 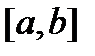 ;
;
2. Найти все стационарные точки функции, и точки, в которых 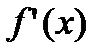 не существует, которые принадлежат
не существует, которые принадлежат 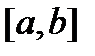 . Обозначим эти точки
. Обозначим эти точки 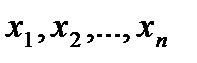 ;
;
3. Вычислить значения 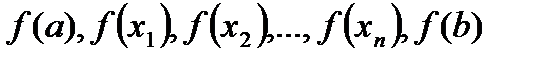 ;
;
4. Сравнить все значения, полученные на предыдущем шаге, и выбрать из них наименьшее и наибольшее.

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция  дифференцируема в точке
дифференцируема в точке 
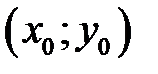 некоторой области
некоторой области 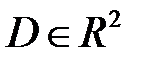 . Рассечем поверхность
. Рассечем поверхность 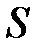 , изображающую функцию
, изображающую функцию 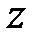 , плоскостями
, плоскостями  и
и  .
.
Плоскость  пересекает поверхность
пересекает поверхность 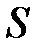 по некоторой линии
по некоторой линии  , уравнение которой получается подстановкой в выражение исходной функции
, уравнение которой получается подстановкой в выражение исходной функции  вместо
вместо  числа
числа 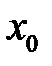 . Точка
. Точка  принадлежит кривой
принадлежит кривой  . В силу дифференцируемости функции
. В силу дифференцируемости функции 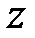 в точке
в точке  функция
функция  также является дифференцируемой в точке
также является дифференцируемой в точке  . Следовательно, в этой точке в плоскость
. Следовательно, в этой точке в плоскость  к кривой
к кривой 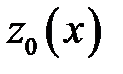 касательная
касательная 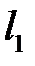 .
.
Проводя аналогичные рассуждения, для сечения  построим касательную
построим касательную  к кривой
к кривой  . Прямые
. Прямые 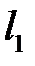 и
и  определяют плоскость
определяют плоскость 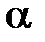 , которая называется касательной плоскостью к поверхности
, которая называется касательной плоскостью к поверхности 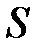 в точке
в точке 
Составим её уравнение. Так как плоскость 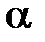 проходит через точку
проходит через точку 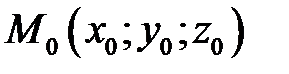 , то её уравнение может быть записано в виде
, то её уравнение может быть записано в виде
 ,
,
которое можно переписать так:
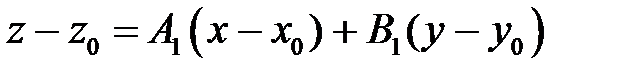 (1)
(1)
(разделив уравнение на 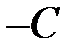 и обозначив
и обозначив  ).
).
Найдем  и
и 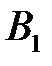 .
.
Уравнения касательных 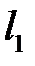 и
и  имеют вид
имеют вид
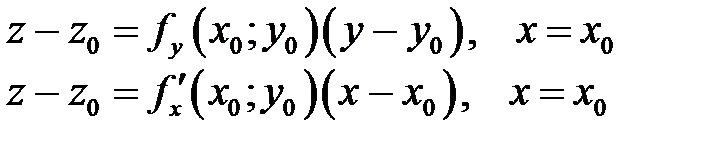
соответственно.
Касательная 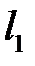 лежит в плоскости
лежит в плоскости 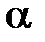 , следовательно, координаты всех точек
, следовательно, координаты всех точек 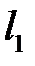 удовлетворяют уравнению (1). Этот факт можно записать в виде системы
удовлетворяют уравнению (1). Этот факт можно записать в виде системы
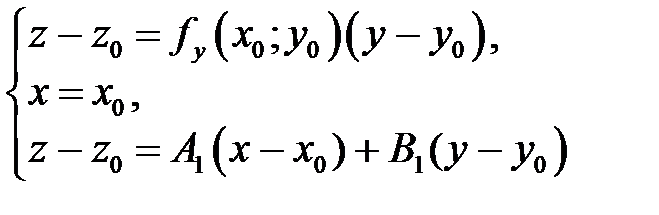 .
.
Разрешая эту систему относительно  , получим, что
, получим, что 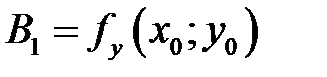 .
.
Проводя аналогичные рассуждения для касательной  , легко установить, что
, легко установить, что 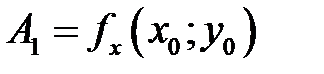 .
.
Подставив значения  и
и  в уравнение (1), получаем искомое уравнение касательной плоскости:
в уравнение (1), получаем искомое уравнение касательной плоскости:
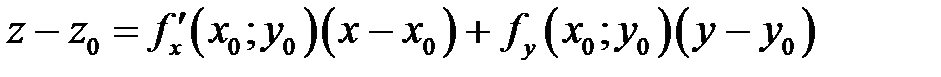 (2)
(2)
Прямая, проходящая через точку  и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется её нормалью.
и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется её нормалью.
Используя условие перпендикулярности прямой и плоскости легко получить каноническое уравнение нормали:
 (3)
(3)
Если поверхность  задана уравнением
задана уравнением  , то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции:
, то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции:
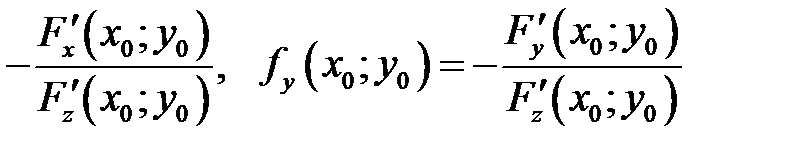

Теорема существования. Если:
1) функция 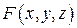 обращается в нуль в некоторой точке
обращается в нуль в некоторой точке 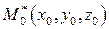 ;
;
2) 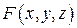 и
и  определены и непрерывны в окрестности точки
определены и непрерывны в окрестности точки 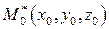 ;
;
3) 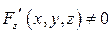 ,
,
то в некоторой достаточно малой окрестности точки  существует единственная однозначная непрерывная функция
существует единственная однозначная непрерывная функция
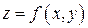 ,
,
удовлетворяющая уравнению
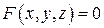
и такая, что  .
.
Частные производные функций, заданных неявно. Если выполнены все условия приведенной выше теоремы и, кроме того, функция 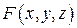 дифференцируема в окрестности точки
дифференцируема в окрестности точки 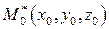 , то функция
, то функция 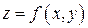 дифференцируема в окрестности точки
дифференцируема в окрестности точки  и ее производные
и ее производные 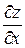 и
и 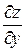 могут быть найдены из уравнений
могут быть найдены из уравнений
 .
.
Если функция 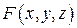 дифференцируема достаточное число раз, то последовательным дифференцированием этих уравнений вычисляются производные высших порядков от функции
дифференцируема достаточное число раз, то последовательным дифференцированием этих уравнений вычисляются производные высших порядков от функции 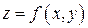 .
.
Дифференцирование неявных функций, заданных системой уравнений. Пусть функции  удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) обращаются в нуль в точке 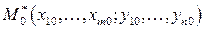 ;
;
2) дифференцируемы в окрестности точки 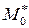 ;
;
3) функциональный определитель (якобиан) 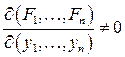 в точке
в точке 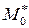 .
.
Тогда система уравнений

однозначно определяет в некоторой окрестности точки  систему дифференцируемых функций
систему дифференцируемых функций
 ,
,  ,
,
удовлетворяющих системе уравнений  и начальным условиям
и начальным условиям
 ,
,  .
.
Дифференциалы этих неявных функций могут быть найдены из системы
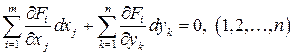 .
.
Вектор  (
( ) является вектором касательной кривой
) является вектором касательной кривой  в точке
в точке  . Обозначим точку кривой
. Обозначим точку кривой 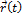 , соответствующую значению параметра
, соответствующую значению параметра  , через P, т.е.P=P
, через P, т.е.P=P  . Плоскость, проходящая через точкуP
. Плоскость, проходящая через точкуP  кривой и перпендикулярная вектору
кривой и перпендикулярная вектору 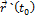 , называется нормальной плоскостью кривой в точке
, называется нормальной плоскостью кривой в точке  .По вектору
.По вектору 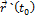 =
=  и точке P
и точке P  запишем уравнения касательной прямой и нормальной плоскости кривой
запишем уравнения касательной прямой и нормальной плоскости кривой 
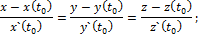
 +
+ 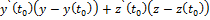 =0.
=0.



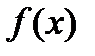 определена и непрерывна на
определена и непрерывна на 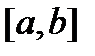 , дифференцирована в
, дифференцирована в  , за исключением конечного количества точек. По первой и второй теоремам Вейерштрасса она ограничена и достигает на этом сегменте своих точных верхней и нижней границ, которые являются ее наибольшим и наименьшим значениями на этом сегменте. Надо эти значения найти.
, за исключением конечного количества точек. По первой и второй теоремам Вейерштрасса она ограничена и достигает на этом сегменте своих точных верхней и нижней границ, которые являются ее наибольшим и наименьшим значениями на этом сегменте. Надо эти значения найти. , или
, или 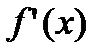 не существует. Это означает, что
не существует. Это означает, что 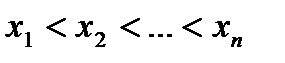 , где
, где  , в каждом из которых уже нет таких точек, где
, в каждом из которых уже нет таких точек, где  , а потому наименьшее и наибольшее значения она будет принимать на концах
, а потому наименьшее и наибольшее значения она будет принимать на концах  .
.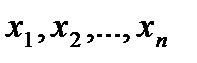 ;
;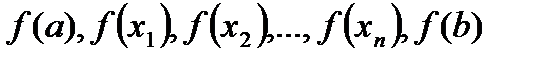 ;
;
 дифференцируема в точке
дифференцируема в точке 
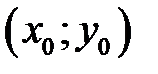 некоторой области
некоторой области 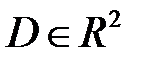 . Рассечем поверхность
. Рассечем поверхность 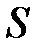 , изображающую функцию
, изображающую функцию 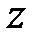 , плоскостями
, плоскостями  и
и  .
. , уравнение которой получается подстановкой в выражение исходной функции
, уравнение которой получается подстановкой в выражение исходной функции  числа
числа 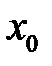 . Точка
. Точка  принадлежит кривой
принадлежит кривой 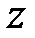 в точке
в точке  функция
функция 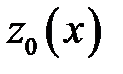 касательная
касательная 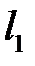 .
. к кривой
к кривой  . Прямые
. Прямые 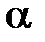 , которая называется касательной плоскостью к поверхности
, которая называется касательной плоскостью к поверхности 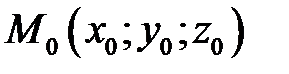 , то её уравнение может быть записано в виде
, то её уравнение может быть записано в виде ,
,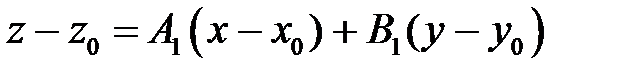 (1)
(1)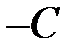 и обозначив
и обозначив  ).
). и
и 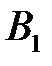 .
.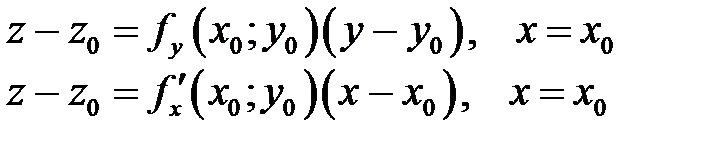
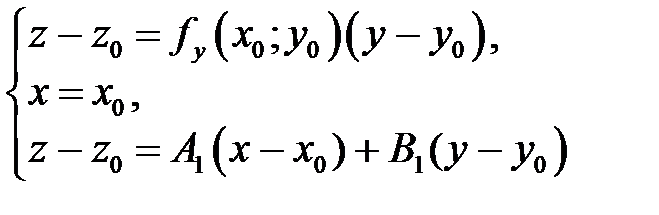 .
. , получим, что
, получим, что 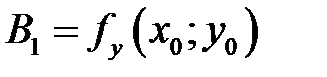 .
.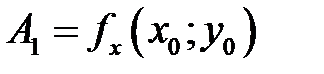 .
. и
и 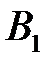 в уравнение (1), получаем искомое уравнение касательной плоскости:
в уравнение (1), получаем искомое уравнение касательной плоскости: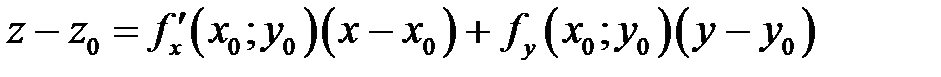 (2)
(2) (3)
(3) , то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции:
, то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции: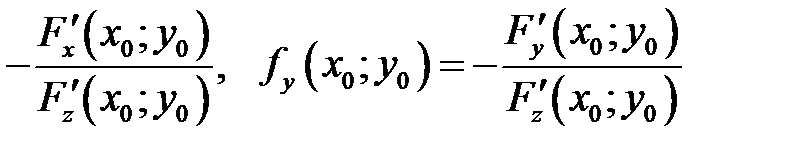

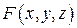 обращается в нуль в некоторой точке
обращается в нуль в некоторой точке 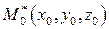 ;
; определены и непрерывны в окрестности точки
определены и непрерывны в окрестности точки 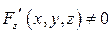 ,
, существует единственная однозначная непрерывная функция
существует единственная однозначная непрерывная функция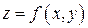 ,
,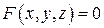
 .
.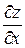 и
и 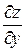 могут быть найдены из уравнений
могут быть найдены из уравнений .
. удовлетворяют следующим условиям:
удовлетворяют следующим условиям: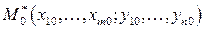 ;
;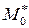 ;
;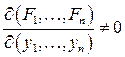 в точке
в точке 
 систему дифференцируемых функций
систему дифференцируемых функций ,
,  ,
, ,
, 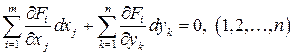 .
. (
( ) является вектором касательной кривой
) является вектором касательной кривой  в точке
в точке 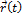 , соответствующую значению параметра
, соответствующую значению параметра  . Плоскость, проходящая через точкуP
. Плоскость, проходящая через точкуP 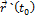 , называется нормальной плоскостью кривой в точке
, называется нормальной плоскостью кривой в точке  и точке P
и точке P  запишем уравнения касательной прямой и нормальной плоскости кривой
запишем уравнения касательной прямой и нормальной плоскости кривой 
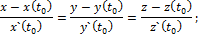
 +
+ 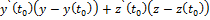 =0.
=0.


