Динамические погрешности при измерении быстроменяющихся, переменных и импульсных давлений, а также при акустических измерениях, определяются временными параметрами исследуемого процесса и динамическими характеристиками датчика или системы датчик–трубопровод.
Большинство датчиков давления с достаточной для инженерных расчетов точностью можно описать дифференциальным уравнением второго порядка и представить кинематической схемой, приведенной на рис. 4.6.
Все датчики давления относятся к преобразователям с силовым возбуждением, когда внешняя сила
F (
t) создается за счет воздействия давления жидкости или газа на ЧЭ датчика: мембрану, мембранную или анероидную коробку, витую пружину или сильфон.
Внешняя переменная сила F (t) воздействует на массу m, связанную с неподвижным корпусом К упругим элементом (например, пружиной), обладающим жесткостью С э. В преобразователе в общем случае предусматривается демпфер (успокоитель), обеспечивающий коэффициент успокоения К у.
Если предположить, что: масса пружины и подвижной части демпфера пренебрежимо мала по сравнению с массой m; конструкция преобразователя допускает перемещение массы m только вдоль оси х (масса m имеет лишь одну степень свободы); успокоитель оказывает сопротивление, пропорциональное первой степени скорости (вязкое трение); в начальный момент времени перемещение х подвижной части и ее скорость dx/dt равны
 (4.7)
(4.7)
При измерении переменных давлений значительные погрешности результатов экспериментов возникают за счет влияния промежуточных объемов, имеющихся между источником давления и ЧЭ датчика. Эти объемы возникают из-за наличия соединительных трубопроводов или каналов между источником переменного давления и датчиком, а также за счет конструктивных особенностей самих датчиков.
Проведем оценку частоты собственных колебаний системы датчик – трубопровод.
При однородном жидкостном или газовом заполнении частота системы датчик – трубопровод [52]
 (4.8)
(4.8)
где f от.тр – частота собственных колебаний трубопровода, заканчивающегося вместо датчика жестким дном («глухой» трубопровод); mi – поправочный коэффициент, учитывающий влияние параметров датчика, трубопровода и заполняющей среды на частоту собственных колебаний системы.
Частота собственных колебаний «глухого» трубопровода
 (4.9)
(4.9)
где с – скорость распространения звука в среде, заполняющей систему (для воздушного заполнения системы при температуре плюс 20°С с = 330 м/с; для системы, заполненной водой, с = 1500 м/с); t – длина трубопровода, м.
Поскольку в реальных системах коэффициент m i всегда меньше единицы, то частота собственных колебаний, рассчитанная по (4.9), является предельной для данной системы и не может превышать этого значения. При больших длинах трубопроводов, т.е. при l > 1 м, частота собственных колебаний реальных систем приближается к частоте собственных колебаний «глухого» трубопровода и поэтому ориентировочно может быть определена по (4.9). Для меньших длин трубопроводов необходимо вводить поправку на коэффициент m i, который при газовом заполнении будет
 (4.10)
(4.10)
где К = V 0/ V т; V 0 – объем приемной полости датчика; V т – объем трубопровода.
Выражение (4.10) справедливо при газовом заполнении для приемных полостей любых видов ЧЭ: мембранных, сильфонных, представляющих собой полые витые пружины и др.
Поправка m i при жидкостном заполнении системы для приемных полостей мембранных датчиков
 (4.11)
(4.11)
где  ;
; 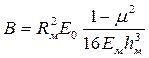 ; L – длина предмембранной полости;
; L – длина предмембранной полости;
R м, h м, Е м – соответственно радиус, толщина и модуль упругости мембраны; Е 0 – модуль упругости жидкости; μ –коэффициент Пуассона для материала мембраны; l, d тр – соответственно длина и внутренний диаметр трубопровода; D м – диаметр мембраны.
При жидкостном заполнении частоту собственных колебаний системы датчик–трубопровод можно рассчитать также по формуле
 (4.12)
(4.12)
где  - модуль упругости соединительного трубопровода, заполненного жидкостью; ρ – плотность жидкости; Е тр – модуль упругости материала трубопровода; δ тр – толщина стенки трубопровода;
- модуль упругости соединительного трубопровода, заполненного жидкостью; ρ – плотность жидкости; Е тр – модуль упругости материала трубопровода; δ тр – толщина стенки трубопровода;
S тр – площадь поперечного сечения трубопровода; S м – площадь мембраны датчика; с – постоянный коэффициент; р — измеряемое давление; у – прогиб центра мембраны, соответствующий действующему на нее давлению; у/р – упругость мембраны; V д – объем предмембранной полости датчика.
Частоту собственных колебаний систем в случае смешанного заполнения определяют по формуле
 (4.13)
(4.13)
где 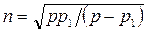 ; р – среднее давление в системе; p 1 – начальное давление в системе; L np= l + V д/ S тр – приведенная длина трубопровода; V д – объем приемной полости датчика; g – ускорение свободного падения; ρ – плотность жидкости.
; р – среднее давление в системе; p 1 – начальное давление в системе; L np= l + V д/ S тр – приведенная длина трубопровода; V д – объем приемной полости датчика; g – ускорение свободного падения; ρ – плотность жидкости.
Под смешанным заполнением понимают заполнение, образующееся в результате присоединения к жидкостному источнику давления предварительно не заполненной жидкостью системы датчик–трубопровод. Воздух, находившийся к началу измерения в объеме системы при атмосферном давлении, сжимается. Образуется смешанное заполнение, состоящее из жидкости и воздушной подушки, поджатой средним давлением жидкостного источника давления.
Значения поправочных коэффициентов mГ для системы с газовым заполнением показаны на рис. 4.7.
Таким образом, при использовании датчиков давления без соединительных трубопроводов и предмембранных полостей их динамическими
характеристиками являются частота собственных колебаний
f 0 и степень успокоения
r, которые, могут быть рассчитаны по формулам:
 (4.14)
(4.14)
– для недемпфированных датчиков;
 (4.15)
(4.15)
– для демпфированных датчиков, где  .
.
При измерении переходных процессов также возникает динамическая погрешность, на оценке которой мы коротко остановимся. Реальный переходной процесс (на рис. 4.8 процесс, показанный сплошной линией
1) можно аппроксимировать двумя прямыми – пунктирные линии
2. При такой аппроксимации выходной сигнал датчика с малой степенью успокоения
r в системах с жидкостным заполнением имеет вид, приведенный на рис. 4.9, причем сигнал с датчика может меняться в зависимости от частоты собственных колебаний
ω 0 измерительного устройства и времени нарастания процесса
Т.
Амплитуда колебаний выходного сигнала по отношению к действительному процессу для всех значений
ω 0 и
Т на участке нарастания давления будет меньше наибольшего выброса в конце процесса нарастания давления. Поэтому в качестве динамической погрешности измерения переходного процесса слабодемпфированными системами с жидкостным заполнением принимают наибольшее значение выброса Δ
р. Для определения зависимости Δ
р от
ω 0 и
Т следует в правую часть дифференциального уравнения (4.7) подставить
F (
t), описывающее идеализированный переходной процесс. Решение такого уравнения для недемпфированиых датчиков (т.е. для преобразователей с
r =0) дает возможность оценить динамическую погрешность
 (4.16)
(4.16)
где Т – время нарастания переходного процесса; ω 0 – круговая частота собственных колебаний датчика.
Таким образом, при малом демпфировании амплитуда колебаний на участке установившегося давления будет целиком определяться только соотношением между временем нарастания переходного процесса и частотой собственных колебаний датчика. На рис. 4.10 приведена зависимость Δ
р от
δ =
Т /
Т 0=
Тω 0/2
π (она изображена сплошной линией). Пунктирная огибающая линия характеризует наибольшее значение динамической погрешности измерения переходного процесса системой, заполненной жидкостью.
В недемпфированных системах датчик–трубопровод, заполненных газом, при измерении переходных процессов выходной сигнал имеет вид графика, приведенного на рис. 4.9 (кривая 3) [55]. Динамическая погрешность в этом случае складывается из двух составляющих: Δ р 1 – погрешности измерения переходного процесса, появляющейся в результате свободных колебаний системы на установившем участке, и Δ р 2 – погрешности, характеризующей запаздывание датчика в сравнении с действительным процессом. На рис. 4.11 приведены кривые, полученные экспериментальным путем Н.И. Ивановой, показывающие зависимости Δ р 1 и Δ р 2 от временных характеристик процесса и параметров датчика. Как видно из рис. 4.11, основной динамической погрешностью при измерении переходного процесса системой с газовым заполнением является погрешность запаздывания Δ р 2 [52]. Для таких систем она больше Δ р 1 и сохраняет свои значения при больших значениях δ = Т/Т о.
Динамические погрешности при измерении переходных процессов систем со смешанным заполнением мало исследованы. Однако из опубликованных материалов следует, что при установившемся давлении р уст>6 МПа динамические погрешности при измерении переходных процессов в системах со смешанным заполнением приближаются к значениям 
погрешностей, возникающих в системах с жидкостным заполнением, а при р уст<1,5 МПа – к погрешностям в системах с газовым заполнением.






 (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10) (4.11)
(4.11) ;
; 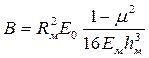 ; L – длина предмембранной полости;
; L – длина предмембранной полости; (4.12)
(4.12) - модуль упругости соединительного трубопровода, заполненного жидкостью; ρ – плотность жидкости; Е тр – модуль упругости материала трубопровода; δ тр – толщина стенки трубопровода;
- модуль упругости соединительного трубопровода, заполненного жидкостью; ρ – плотность жидкости; Е тр – модуль упругости материала трубопровода; δ тр – толщина стенки трубопровода;  (4.13)
(4.13)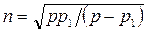 ; р – среднее давление в системе; p 1 – начальное давление в системе; L np= l + V д/ S тр – приведенная длина трубопровода; V д – объем приемной полости датчика; g – ускорение свободного падения; ρ – плотность жидкости.
; р – среднее давление в системе; p 1 – начальное давление в системе; L np= l + V д/ S тр – приведенная длина трубопровода; V д – объем приемной полости датчика; g – ускорение свободного падения; ρ – плотность жидкости.
 (4.14)
(4.14) (4.15)
(4.15) .
.

 (4.16)
(4.16)




