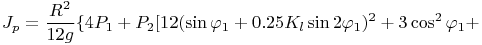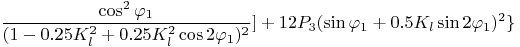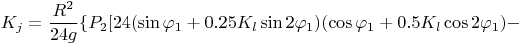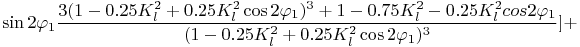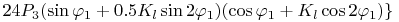Особенности дифференциального описания систем

 

А сейчас давайте рассмотрим возможности различных подходов (импульсного, силового, мощностного и энергетического) для получения текущего дифференциального описания явлений Природы. Здесь сразу отпадают импульсный и энергетический подходы, т.к. нам надо получить уравнение описывающее текущее (мгновенное) поведение системы, а эти подходы могут дать описание только используя значения импульса и энергии в начальном и конечном состояниях системы. Мне могут возразить, что энергетический подход с использованием лагранжиана L=T-U (3) позволяет получить дифференциальные уравнения для описания системы. Но здесь мы имеем энергетический подход не в чистом виде, а его суррогат, т.к. по сути используется силовой подход, а все эти манипуляции с кинетической энергией системы нужны только для того, чтобы получить выражение для силы инерции действующей по обобщенным координатам и, если у нас имеется и потенциальная энергия, то и для силы от взаимодействия системы с этим полем. А потом уже к этим двум силам, если необходимо, добавляются и другие обобщенные силы, действующие на эту систему, т.е. используется силовой подход, т.к. при энергетическом подходе никаких сил не должно быть, как это у нас и было при описании процесса движения двух ракет с использованием энергетического подхода.

 

А если мы производим описание явлений Природы не в обобщенных координатах, а в обычной декартовой системе координат, то нет никакой необходимости в манипуляциях с энергиями в обобщенных координатах и мы можем сразу, используя силовой подход Эйлера (33), записать, что сила инерции по каждой из осей координат равна силе взаимодействия нашего тела с потенциальным полем. А потом, используя этот же силовой подход, добавлять к этим двум силам, если необходимо, и другие силы, действующие на тела системы, поведение которой мы описываем. При этом, если мы будем описывать явления Природы в декартовой системе координат, то манипуляции Гамильтона (3) с его лагранжианом упростятся до выражения (32), т.к. кинетическая энергия будет зависеть только от скорости, а потенциальная энергия только от координат и поэтому отпадает необходимость проводить все манипуляции Эйлера для получения уравнений экстремалей в геометрических задачах, которые Лагранж тупо перенес на задачи механики. Но, я думаю, что многие будут поставлены в тупик, если попробуют получить с использованием даже этих упрощенных манипуляций (32) дифференциальное уравнение для описания движения топливной ракеты. Хотя здесь у нас не будет ни потенциальной энергии, ни внешних сил, действующих на систему, а кинетическая энергия системы у нас будет состоять только из энергии ракеты и энергии газов.

 

d(dL/dVr)/dt - dL/dR =0 (3)

d(dT/dVr)/dt + dU/dR =0 (32)

m*d2R/dt2 - Fr = 0 (33)

 

К тому же надо отметить, что описание систем в обобщенных координатах имеет практический смысл только для самых элементарных систем, которые и рассматриваются в учебниках, и к тому же при этом и информации от такого решения мы получаем самый минимум, который нас не устраивает при решении практических задач. А само описание в обобщенных координатах, даже для простейших реальных систем, получается просто умопомрачительное, поэтому при решении реальных задач никто, имеющий хоть пару извилин, не будет использовать энергетическо-геометрический подход Лагранжа с его обобщенными координатами. И, чтобы в этом убедится, я рассмотрю ниже описание с использованием энергетическо-геометрического подхода Лагранжа обычного кривошипно-шатунного механизма. А вообще-то, с использованием манипуляций с лагранжианом мы не можем описать ни одной механической системы, т.к. в реальных условиях в любых системах всегда будут силы трения, т.е. будет диссипация энергии, а в этом случае эти манипуляции нельзя использовать, т.к. в этом случае нельзя применять ПНД, из которого они и вытекают.

 

Но это нисколько не смущает математико-физиков и Ландау, который является ярым сторонником Лагранжа и на стр. 97 [2] своего культового для СССР учебника просто заявляет, что «Процесс движения в этих условиях уже не является чисто механическим процессом». Таким образом, если механическая система не описывается функцией Лагранжа, то для Ландау это уже не механика (правда он употребляет термин не классическая механика). Но позвольте, мы не знаем ни одной механической системы, где бы отсутствовало трение, т.е. получается, что Механика Ландау не имеет никакого отношения к реальной механике. Единственная область, где, как пишет Фейнман, отсутствует трение это механика микромира и, таким образом, получается, что вся Механика Ландау нужна только для квантовой механики. Хотя и здесь не все так однозначно, т.к., например, тормозное излучение электрона, которое, по сути, является той же диссипацией энергии, никто вроде не отрицает. И получается, что и в квантовой механике Механика Ландау не применима. А тогда вообще не понятно о механике для какой галактики он написал свой учебник. Но Ландау пытается все же обосновать то, что его Механика нужна физике именно для нашей галактики, и вот что он пишет:

 

«Если при скольжение трение настолько мало, что им можно вовсе пренебречь, то поверхности тел называются абсолютно гладкими. Напротив, если свойства поверхности допускают лишь чистое качение тел без скольжения, а трением при качение можно пренебречь, то поверхности называются абсолютно шероховатыми.

В обоих случаях силы трения не фигурируют явным образом в задаче о движении тел, и по этому задача является чисто механической. Если же конкретные свойства трения существенны для движения, то последнее не является уже чисто механическим процессом (ср. §25).»

А теперь упритесь большим пальцем правой руки в абсолютно гладкий стол и быстро проведите рукой справа налево - у вас возникнут автоколебания большого пальца, но Ландау не научит Вас решать эту элементарную механическую задачку, потому что по его классификации это не механическая задача. Да, Ландау в совершенстве владел интегральным и дифференциальным исчислениями, и здесь рядом с ним можно поставить разве что Эйлера и Лагранжа, но объявлять механикой только те явления, которые описываются дифференциальными уравнениями вытекающими из ПНД, т.е. обязательно без трения и которые он может решить, в корне неверно. Но при этом, как ни странно, он рассматривает и движения тел в среде, т.е. с диссипацией энергии, отводя им шесть параграфов в своей Механике (25...30), хотя и не считает такие задачи механическими. А объяснение здесь простое. Для частного случая, когда сопротивление среды пропорционально скорости в первой степени, оказывается дифференциальные уравнения для описания таких систем, хотя и не получаются из его любимого ПНД, но они получаются с помощью манипуляций, которые он придумал для диссипативной функции, линейным а в этом случае он их может решить и, следовательно, этому он и будет учить своих читателей. Таким образом, и трение, по большому счету, не является препятствием для отнесения таких систем к механическим, т.е. механикой у Ландау являются только те процессы при описание которых он может продемонстрировать свои математические способности. А вот, когда он рассматривает различные механические системы, где всегда присутствует в основном сухое трение (или скольжения или качения), то он на стр.162 объявляет эти системы уже точно не механическими (такие уравнения не решаются аналитически) и поэтому дальше он будет учить читателей решать только механические задачи, т.е. получается что он будет учить решать приблизительные (учебные) механические задачи, где сухого трения нет. Отсюда можно сделать вывод о том, что то, что выгодно лично Ландау, то правильно, а то, что не выгодно, это не правильно, т.е. в Механике Ландау действуют уже не законы точных наук, а политические законы, где то, что выгодно, например, Америке, это правильно, а то, что не выгодно, это не правильно.

 

А теперь давайте рассмотрим описание с использованием энергетическо-геометрического подхода Лагранжа обычного кривошипно-шатунного механизма (КШМ), изображенного на рис. 7. Здесь у нас только одна обобщенная координата - угол поворота кривошипа. Я не буду давать вывод дифференциального уравнения, т.к. он еще более громоздкий, чем получившийся ответ, и приведу только дифференциальное уравнение для ускорения угла поворота кривошипа.

 

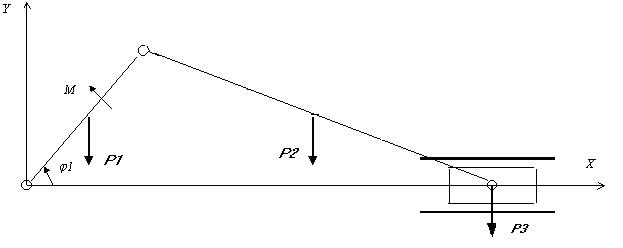
Рис. 7. Расчетная схема кривошипно-шатунного механизма для описания по обобщенным координатам.

 

Кого интересуют подробности вывода этого дифференциального уравнения, могут ознакомиться с этим в файле krivo1 (или в формате .mws для работы с математическим пакетом Maple 9.5 или в формате .html для просмотра в браузере). Естественно, студентов такими уравнениями не пугают, поэтому в учебниках - например, у Ландау - дают вывод дифференциальных уравнений для самых простеньких систем. Но для инженеров-механиков всё же кое-что дают и по таким сложным системам, как КШМ, хотя и в этом случае дают упрощённый вывод, т.е. с различными упрощениями - как, например, здесь [29]. Но в этом случае получается малопригодное для практического использования уравнение (34):

 

(34)

 

 

 

 

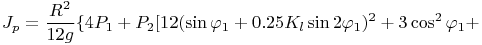
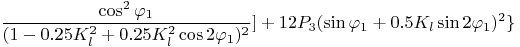
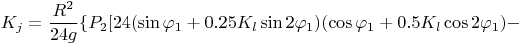
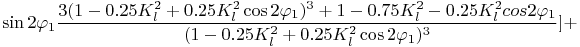
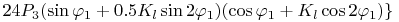
где Jp - приведённый момент инерции системы; Kl, Kj - коэффициенты ( Kl = R / L ); R - радиус кривошипа; L- длина шатуна; M - момент сопротивления приложенный к кривошипу (маховику); P1 , P2 , P3 - соответственно вес кривошипа, шатуна и поршня; g - ускорение свободного падения. Кого интересуют подробности вывода и этого упрощенного дифференциального уравнения, могут ознакомиться с этим в файле krivo2 (или в формате .mws для работы с математическим пакетом Maple 9.5 или в формате .html для просмотра в браузере). А с результатами, которые можно получить с использованием этого дифференциального уравнения, можно ознакомиться, проведя вычислительные эксперименты на математической квазимодели КШМ в программе Krivoship1, где используется это уравнение. Для этого надо в рамке <Метод получения уравнений> выбрать переключатель <уравнений Лагранжа 2-го рода> (скачать программу можно с моих сайтов в разделе Программы, где можно также скачать и архивы файлов krivo1 и krivo2).

 

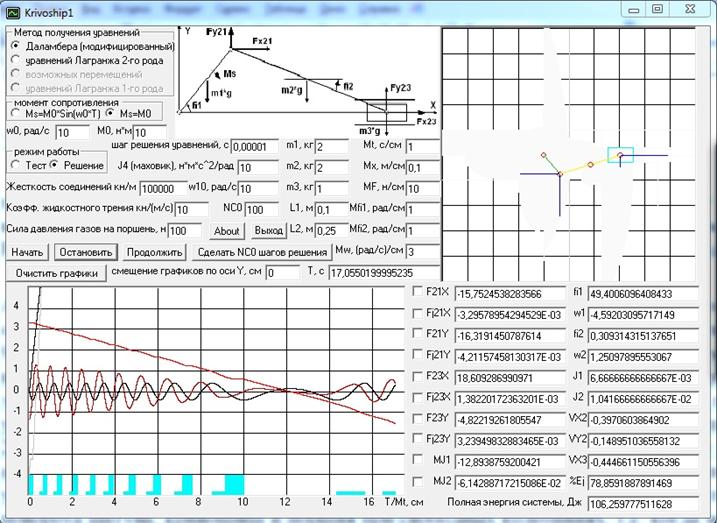
Рис. 8. Моделирование работы КШМ по описанию, полученному с использованием силового подхода. Скриншот программы Krivoship1.

 

Вот только ничего интересного о системе с использованием этого уравнения узнать не получится, т.к. единственное, что это уравнение может дать, это скорости и углы поворота шатуна и кривошипа и перемещение поршня при свободных колебаниях, т.е. когда момент сопротивления равен нулю и на поршень не давят газы. А, чтобы посмотреть, как будут изменяться эти углы и скорости под нагрузкой, нам надо задать еще момент сопротивления и внешние силы, т.е. силы давления газов на поршень, которые будут изменяться по определенному алгоритму. Конкретно в программе Krivoship1 задан алгоритм работы двухтактного двигателя, где весь рабочий цикл совершается за один оборот кривошипа, а на рис. 8 Вы видите, что вследствие того, что работа момента сопротивления больше работы совершаемой поршнем, у нас скорость вращения кривошипа постепенно уменьшается и в конце-концов начинается его вращение в другую сторону.

 

В общем-то, чтобы определить скорости и углы поворота шатуна, кривошипа и перемещение поршня, как при свободных колебаниях, так и под нагрузкой, не обязательно решать аналитически уравнение (34) и можно его решить численными методами, что и делается в программе Krivoship1. Но вот для того, чтобы определить усилия, возникающие в элементах КШМ, необходимо обязательно сначала решить уравнение (34) аналитически, а потом составить для этой системы еще уравнения Лагранжа 1-го рода и уже, решив их, найти усилия, возникающие в элементах системы. Хотя и тут есть один вариант решения, который я применяю для описания явлений Природы при использовании силового или мощностного подходов. А конкретно, мы можем сразу и решать дифференциальные уравнения, полученные с использованием энергетическо-геометрического подхода Лагранжа, и находить усилия, возникающие в элементах системы, если соединим элементы системы упругими связями. И хотя при этом у нас формально должно получится еще в два раза больше уравнение (34), т.к. теперь у нас в системе будет и потенциальная энергия в этих соединениях, но теперь у нас получается, что не будет самих обобщенных координат, т.к. теперь все элементы соединены друг с другом не жестко.

 

Таким образом, у нас исчезло единственное достоинство энергетическо-геометрического подхода Лагранжа - а именно, наличие минимального числа дифференциальных уравнений для описания систем. И теперь для описания КШМ надо будет использовать 5 координат, но это единственная возможность не только сразу решать дифференциальные уравнения и находить усилия в элементах системы. Более того, теперь мы можем найти даже резонансные частоты системы, хотя сделать это, решая дифференциальные уравнения аналитически, будет очень не просто и, к тому же, толку от этого будет очень мало, т.к. мы все равно не узнаем какие будут на этих частотах динамические нагрузки. А вот, если мы будем решать эту систему дифференциальных уравнений численными методами, то мы получим исчерпывающую информацию о динамических нагрузках возникающих не только при нормальных режимах работы систем, но и в режимах резонансов и биений.

 

И тут возникает вопрос, а зачем нам теперь надо для дифференциального описания нашей системы использовать манипуляции (32), если точно такое же описание мы можем получить, используя уравнения Эйлера (33)? Ведь теперь нам надо проделывать манипуляции (32) пять раз для каждой из координат, по которым теперь описывается движение элементов системы, а сделать это на несколько порядков проще с использованием уравнения (33). Поэтому я всегда применяю именно такой метод для дифференциального описания явлений Природы (или искусственно созданных систем), а для описания конкретно КШМ система дифференциальных уравнений, описывающих его поведение, будет выглядеть как (35), где: J1 = m1 * R^2 / 3 - момент инерции кривошипа относительно оси вращения, J2 = m2 * L^2 / 12 момент инерции шатуна относительно его оси вращения и L1 = L / 2 - половина длины шатуна L. Расчетная схема для этого описания приведена на рис. 9.

 

Рис. 9. Расчетная схема кривошипно-шатунного механизма для описания по декартовым координатам.

 

J1*d2j1/dt2 = Fy21*R*cos(j1) - Fx21*R*sin(j1) - Mс - m1*g*R*cos(j1) / 2

m2*d2X2/dt2 = - Fx21 - Fx23

m2*d2Y2/dt2 = - Fy21 - Fy23 - m2*g

J2*d2j2/dt2 = (Fy21 - Fy23)*L1*cos(j2) - (Fx21 + Fx23)*L1*sin(j2) (35)

m3*d2X3/dt2 = Fx23 - Fg если cos(j1) < 0 то Fg = 0

если cos(j1) > 0 и sin(j1) > 0 то Fg = Fmax

если cos(j1) > 0 и sin(j1) < 0 то Fg = 0.2*Fmax

 

При этом движение кривошипа опишем одним уравнением, как его вращением вокруг оси Z, движение шатуна опишем тремя уравнениями: движением его центра масс по осям X и Y и вращением шатуна вокруг оси Z проходящей через его центр масс, а движение поршня опишем одним уравнением вдоль оси X. Здесь у меня Fg это сила давления газов в камере сгорания на поршень, которая при рабочем ходе будет Fmax, при сжатии рабочей смеси будет 0.2*Fmax, а при выпуске отработавших газов и при всасывании рабочей смеси Fg = 0. Условия изменения этих сил сформулированы из условия, что двигатель двухтактный, т.е. весь цикл в двигателе проходит за один оборот кривошипа. В этих уравнениях не хватает выражений для определения сил возникающих в упругих элементах, соединяющих элементы системы, которые надо вычислять по уравнениям (36). Как все это будет вычисляться при аналитическом решении этой системы я не знаю и никому этим заниматься не советую, но если очень хочется, то я бы все же порекомендовал делать это не на листочке бумаги, а перепоручить это решение какому ни будь математическому пакету символьных вычислений. А вот при численном решении этой системы уравнений (35) необходимо вычислить по уравнениям (36) значения сил перед тем, как обращаться к системе дифференциальных уравнений. Причем, если Вы будете решать систему дифференциальных уравнений методом Рунге-Кутта по 4-м коэффициентам, т.е. будете 4-е раза обращаться к этой системе дифференциальных уравнений, то и силы надо будет тоже вычислять 4-е раза.

X12 = R * cos j1 Y12 = R * sin j1

X21 = X2 - L1 * cos j2 Y21 = Y2 - L1 * sin j2

X23 = X2 + L1 * cos j2 Y23 = Y2 + L1 * sin j2

Fx21 = (X21 - X12) * C12 Fy21 = (Y21 - Y12) * C12

Fx23 = (X23 - X3) * C23 Fy23 = (Y23 - Y3) * C23            

                                  (36)

 

Здесь C12, C23 - радиальная жесткость шарниров соединяющих шатун с кривошипом и шатун с поршнем соответственно, X12 ,Y12 – координаты центра шейки кривошипа контактирующей с шатуном, X21 ,Y21 - координаты центра головки шатуна контактирующей с шейкой кривошипа, X23,Y23- координаты центра головки шатуна контактирующей с поршневым пальцем и X3,Y3- координаты центра поршневого пальца (Y3=0), которые определяются согласно расчетной схеме на рис. 10. При этом принято, что деформируются элементы головок шатуна, а шейка кривошипа и палец поршня приняты абсолютно жесткими, но при необходимости возможны и другие варианты расчета.

 

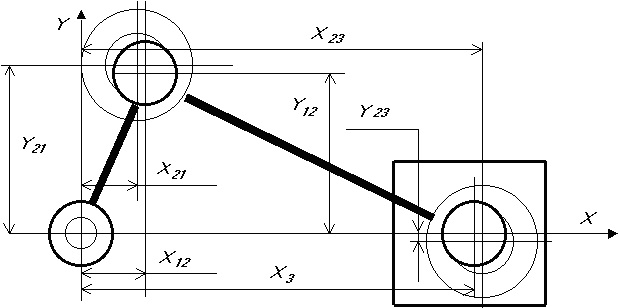
Рис. 10. Схема для определения сил в местах контакта элементов кривошипно-шатунного механизма.

 

При этом в любой системе всегда присутствует трение. Причем видов трения очень и очень много, а природа сил трения пока не известна, но с помощью различных аппроксимаций мы можем чисто количественно описать многие эти процессы вполне удовлетворительно [5]. Например, хорошо аппроксимируются сухое трение и жидкостное (линейное и квадратичное), но, если нет необходимости учитывать конкретный вид трения, то проще всего учесть при дифференциальном описании линейное жидкостное трение. Это позволяет не только более качественно описать конкретные системы, но и позволяет сгладить при резких скачках нагрузки сильные колебания элементов системы на упругих элементах соединяющих части системы. При учете жидкостного трения в местах контактов элементов систем в уравнениях (36) добавятся скорости концов шатуна и кривошипа (скорость поршня известна) и возникающие в этих двух шарнирах силы жидкостного трения при заданных значениях коэффициентов жидкостного трения Kj12 и Kj23 (37), где w1= dj1/dt – угловая скорость вращения кривошипа, а w2= dj2/dt – угловая скорость вращения шатуна относительно его центра масс. Обычно, если это не вытекает из задач исследования, я принимаю значения этих коэффициентов для всех соединений одинаковыми (точно также, как и значения податливости (величина обратная жесткости) всех деталей в местах контакта).

 

VX12 = - w1 * R * sin j1 VY12 = w1 * R * cos j1

VX21 = VX2 + w2 * L1 * sin j2 VY21 = VY2 - w2 * L1 * cos j2

VX23 = VX2 - w2 * L1 * sin j2 VY23 = VY2 + w2 * L1 * cos j2

Fx21j = (VX21 -VX12) * Kj12 Fy21j = (VY21 - VY12) * Kj12

Fx23j = (VX23 -VX3) * Kj23 Fy23j = (VY23 - VY3) * Kj23

Fx21 = Fx21 + Fx21j Fy21 = Fy21 + Fy21j

Fx23 = Fx23 + Fx23j Fy23 = Fy23 + Fy23j

                           (37)

 

Таким образом, мы видим, что при силовом подходе дифференциального описания явлений Природы и искусственных систем весь процесс получения дифференциальных уравнений сводится к простейшему набору одних и тех же операций при описании движения по каждой из декартовых координат и по углам поворота относительно этих осей (тоже самое относится и к описанию в приращениях). И при этом мы получаем именно математическую модель явления или системы, а не квазимодель (34) которая получается при использовании уравнений Лагранжа 2-го рода для описании систем по минимальному количеству обобщенных координат. При этом необходимо вспомнить и ещё одно основное отличие модели от имитатора, которое заключается в том, что модель способна к совершенствованию, т.е. к усложнению или уточнению без переделки всей модели, а новый имитатор (в нашем случае это квазимодель, полученная с использованием манипуляций Лагранжа), можно создать только пройдя весь путь по созданию описания заново. Например, в математической модели можно изменить конструкцию кривошипа и это затронет только уравнения связанные с описанием его движения совершенно не касаясь уравнений, описывающих движение поршня и шатуна. А для получения описания с помощью методов предложенных Лагранжем необходимо при любом конструктивном изменении в системе провести почти все математические выкладки по получению уравнений, описывающих поведение системы, заново, что является явным признаком имитатора.

 

При этом ради справедливости стоит заметить, что во времена Лагранжа его энергетическо-геометрический подход, т.е. не его основное уравнение динамики, которое, к тому же было и ошибочным, а его чисто математический прием, позволявший сократить число дифференциальных уравнений, описывающих поведение систем, до минимума, т.е. до минимального количества обобщенных координат, имел практический смысл. Ведь силовой подход Эйлера для описания явлений Природы давал математическое описание только в декартовой системе координат и для сложных систем получалось очень много уравнений, решить которые совместно было не всегда возможно и надо было, используя другие математические приемы, потом сокращать число этих уравнений, а энергетическо-геометрический подход Лагранжа позволял получить сразу минимально возможное число дифференциальных уравнений. Но все это имеет значение только при аналитическом решении этой системы дифференциальных уравнений, а с появлением компьютеров, когда мы можем применять и численные методы их решения, это уже не имеет никакого значения. И я, например, в своей программе Solsys элементарно решаю численными методами систему из 33 дифференциальных уравнений второго порядка, которые описывают поведение планет Солнечной системы.

 

Как я уже писал выше, для получения дифференциального описания можно использовать не только силовой подход, но и мощностной, т.к. при этом тоже используется баланс для мгновенных мощностей, как и при силовом подходе для мгновенных сил. При этом мощностной подход позволяет нам записывать уравнения мощностного баланса и в функции энергии деленной на время и в функции силы умноженной на скорость. Выше я использовал уравнение мощностного баланса, которое получается из энергетического баланса путем деления энергий на время (только энергии я брал не в начале и конце разгона, как при энергетическом подходе, а средние на интервале Δt), но можно было и силы умножить на скорость. Вот только в данном частном случае (разгона ракеты) у нас мощностной подход, как это часто бывает вырождается в силовой, но так бывает не всегда и при рассмотрении вопроса качения колеса я покажу, что в этом случае применим только мощностной подход, а силовой подход не возможен. При описании топливной ракеты в приращениях мы использовали мощностной подход в записи (38), но его можно было выполнить и в записи (39). Вот только в последнем случае у нас обе части баланса сокращались на Vsr и мы приходим к силовому балансу (13-3).

 

 

(m1-mg1*Δt /2)*Vsr*ΔV/Δt = P + mg1*Vsr^2/2 - mg1*Vg^2/2 (38) мощностной

 

Vsr*(m1-mg1*Δt /2)*ΔV/Δt = Vsr*mg1*Vgo (39) мощностной

 

(m1-mg1*Δt /2)*ΔV/Δt = mg1*Vgo (13-3) силовой

 

Но мощность можно выразить и как произведение крутящего момента на угловую скорость и вот именно эта особенность и позволяет с использованием мощностного подхода правильно описать процессы качения колеса. Сразу замечу, что даже более-менее корректно описать движение колеса на порядок сложнее, чем описать работу атомного реактора или движение ракеты, поэтому я дам очень упрощенное описание этого процесса. А, кого интересуют подробности, я отсылаю к своей диссертации [5]. При этом уравнение мощностей нам здесь понадобится два раза. Сначала мы с его использованием найдем момент сопротивления качению одного колеса, а потом определим силу, действующую на ось колеса в горизонтальной плоскости при наличии внешних горизонтальных сил. Начнем с момента сопротивления качению одного колеса. В учебниках его определяют как произведение мифической силы сопротивления качению колеса на его динамический радиус, но на самом деле никакой силы сопротивления качению не существует. Вот только с использованием силового подхода авторы учебников не смогли придумать ничего другого, как мифическую силу сопротивления качению колеса так же, как раньше изобретали живые и мертвые силы, о чем я писал выше, а также силу пищеварения, силу любви, силу разума и т.д. Давайте рассмотрим на рис. 11 силы и моменты, которые будут на самом деле действовать при равномерном качении ведущего колеса полноприводных трактора или автомобиля при их равномерном движении по несминаемому основанию.

 

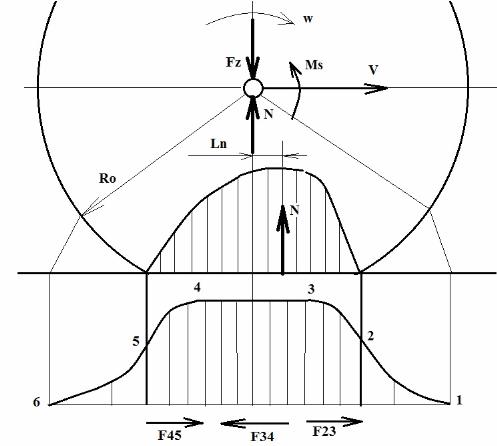
Рис. 11. Схема к расчету момента сопротивления качению ведущего колеса при отсутствии внешних горизонтальных сил и эпюры нормальных напряжений в пятне контакта (вверху) и окружного сжатия шины (внизу).

 

Во-первых, посмотрим на эпюру нормальных напряжений в пятне контакта. Здесь мы видим, что из-за гистерезисных потерь внутри материала шины центр тяжести эпюры смещен в переднюю часть и, следовательно, сила давления опорного основания N будет смещена на величину Ln, что даст момент сопротивления качению N*Ln. А теперь давайте посмотрим на эпюру окружного сжатия шины, которое возникает вследствие того, что длина деформированной окружности стала меньше и теперь элементы шины, расположенные по ее периметру, уменьшили свою длину на участке от точки 1 до точки 6 и длина окружности деформированной шины уже не равна 2*pi*Ro. При этом от точки 1 до точки 3 идет окружное сжатие протектора, а от точки 4 до точки 6 идет восстановление нормального расстояния между соседними элементами протектора. Это приводит к тому, что в пятне контакта от точки 2 до точки 3 возникают касательные напряжения из-за того, что эти элементы протектора притягиваются к средней части протектора 3-4, и возникает в пятне контакта касательная сила F23. А на участке 4-5 у нас элементы протектора наоборот отталкиваются от средней части протектора 3-4 и тоже возникает в пятне контакта касательная сила F45. При этом средняя часть протектора будет практически неподвижна относительно опорного основания, хотя, незначительное смещение, необходимое для возникновения силы трения покоя, все же будет возникать, и эта сила трения покоя F34 будет равна сумме сил F23 и F45 и направлена будет в противоположную от них сторону, т.е. для пятна контакта это будут внутренние силы, которые не будут создавать горизонтальной силы сопротивления качению колеса. Но ведь работу то эти силы в пятне контакта будут совершать и на это должна расходоваться часть энергии подводящейся к колесу через крутящий момент. Расписывать подробно, как я, разбив пятно контакта на множество маленьких участков, находил смещение относительно опорного основания каждого участка, а потом по нормальным напряжениям находил касательные напряжения на этих участках и силу трения, а потом по скорости проскальзывания этих участков относительно опорного основания находил мощность рассеянную в пятне контакта, я не буду. Скажу только, что при желании эту мощность P25 определить можно и, следовательно, зная угловую скорость вращения колеса w, можно найти момент сопротивления при качении колеса, который, исходя из мощностного подхода, определится как

 

Ms= N*Ln + P25/w (41)

 

А теперь давайте рассмотрим ошибку, которая возникает при использовании силового подхода, при рассмотрении вопроса качения колеса при действии на него ещё и внешних горизонтальных сил. Такими силами будут сила инерции Fj трактора или автомобиля при их ускоренном движении, силы сопротивления Fsот ведомых колес или колес прицепа, которые, чтобы они крутились, надо или толкать или тащить, и касательная сила Fk, возникающая в пятне контакта. При этом силы Fj и Fs передадутся колесу через ось колеса и в сумме дадут силу Fe, которая будет действовать уже непосредственно на массу колеса в горизонтальной плоскости. Тогда движение колеса в горизонтальной плоскости опишется уравнением

 

m*dV/dt=Fk-Fe (42)

 

Но сила Fk теперь уже не будет равна нулю, как это у нас было при равномерном качение одного колеса, т.к. теперь у нас в пятне контакта на участке 3-4 элементы протектора тоже будут или частично или полностью смещаться в ту же сторону, что и элементы протектора на участках 2-3 и 4-5. Подробно расписывать как в этом случае по смещениям элементов протектора вычислять касательную силу Fk и мощность P25, которая будет немного отличаться от подсчитанной при свободном качении колеса, я опять не буду, а только констатирую, что при желании определить их можно. Естественно, в учебниках о том, как определять силу Fk, ничего не написано и дается только формула для определения максимально возможного значения этой силы, как произведение веса трактора или автомобиля, приходящихся на эту ось, на коэффициент сцепления шины с конкретным опорным основанием.

 

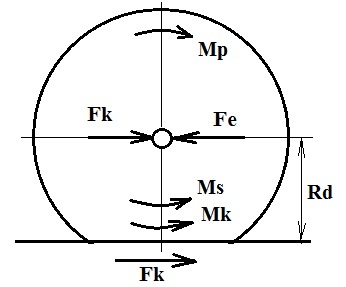
Рис.12. Взаимодействие ведущего колеса автомобиля или трактора с несминаемым опорным основанием при наличии внешних горизонтальных сил.

 

Но допустим, что авторы учебников, используя мои формулы, определили эту силу. Что они предлагают дальше для описания движения колеса. А они предлагают определять момент сопротивления, приложенный к колесу от воздействия касательной силы Fk, при переносе ее по правилам теоретической механики к цетру масс колеса, т.е. к полуоси, как Mk = Fk*Rd, где Rd это динамический радиус качения колеса (расстояние от опорной поверхности до оси вращения колеса при его движении). И в таком случае у нас вращение колеса опишется дифференциальным уравнением

 

Jk*dw/dt = Mp - Mk - Ms ( 43)

 

Здесь у нас Jk это момент инерции колеса, а Mp это момент приложенный к колесу со стороны полуоси. Но давайте внимательно приглядимся к мощности, которую сила Fk передает колесу для его движения в горизонтальной плоскости. Эта мощность будет Fk*V и, следовательно, эта же мощность должна затрачиваться колесом при его вращении как Mk*w, отсюда находим, что Mk= Fk*V / w = Fk*Rk. Здесь Rk это кинематический радиус, который определяется как Ro*(1-ξ), где ξ это максимальное окружное сжатие шины в пятне контакта. Таким образом, т.к. Rk совершенно не равно Rd, то и момент сопротивления от касательной силы Mk = Fk*Rd, определяемый в учебниках исходя из силового подхода, тоже подсчитывается не правильно. Да, колесо выступает в данном случае в роли сложного редуктора трансформирующего угловую скорость в поступательную и силу в крутящий момент, а поэтому правильно описать эти процессы можно только с использованием мощностного подхода. А кому интересно ознакомится с дифференциальным описанием движения всего автомобиля или колесного трактора, могут посмотреть это здесь [5].