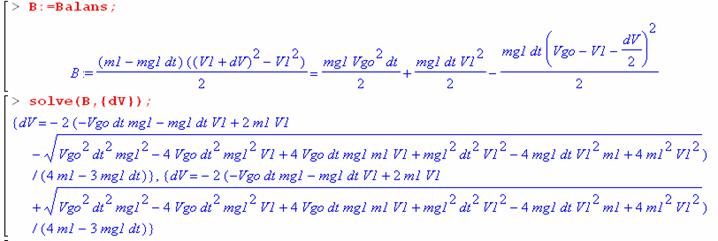Методы математического описания систем

 

Теперь я остановлюсь на особенностях различных подходов для описания явлений Природы при использовании различных методов описания. Начнем с того, что описание явлений Природы на языке математики может быть или интервальным или мгновенным. При интервальном описании мы описываем два положения системы на концах или интервала времени или интервала координат или интервала скоростей системы, используя законы сохранения энергии, количества движения (импульса) или момента количества движения. А при мгновенном описании мы используем дифференциальные уравнения для вторых производных от координат по времени, т.е. для ускорений элементов системы в текущий момент времени, т.е. используя принцип Даламбера или в силовом прочтении Эйлера (2-ой закон Ньютона), или в моем мощностном прочтении. При этом интервальное описании может быть и единичным (конечным), когда мы описываем систему на концах интересующих нас интервалов координат, скоростей или времени, и последовательным (текущим) когда мы разбиваем весь интервал на множество подинтервалов и используем формулы для нахождения приращений скоростей элементов системы при небольшом приращении времени или для нахождения приращения времени необходимого для заданного приращения скорости на этих подинтервалах. Далее я первое интервальное описание буду называть конечным описанием, а второе описанием в приращениях.

 

При этом и мгновенное описание системы, которое я буду называть дифференциальным, и описание в приращениях будут оба текущими описаниями и поэтому могут заменять друг друга, т.е. будут практически эквивалентными. И в тоже время они оба будут аналитическими описаниями в отличие от словесного описания явлений Природы в Началах Ньютона. Но при этом не надо путать аналитическое описание с аналитическим решением. При дифференциальном описании явлений Природы у нас может быть, как общее решение задачи, которое мы привыкли называть аналитическим решением, так и частное решение задачи, когда мы решаем задачу (дифференциальные уравнения, описывающие поведение системы) численными методами. А вот при описании явлений Природы в приращениях у нас изначально заложено только частное решение задачи, т.е. как бы численными методами. Но в отличие от численного решения дифференциальных уравнений, например, методом Эйлера или методом Рунге-Кутта, при численном решении задачи описанной в приращениях нам не нужны никакие дополнительные методы решения, т.к. само описание в приращениях дает нам и метод численного решения.

 

При этом конечное описание ничего не говорит нам о том, что происходило в системе между ее начальным положением и конечным, а текущее описание подробно описывает поведение системы на всем интервале времени между начальным и конечным положениями системы. Например, у нас есть камень, который находится на высоте h=80 м и нам надо узнать какая будет у него скорость, когда он достигнет Земли. Здесь при конечном описании мы записываем закон сохранения энергии m*V^2/2=m*g*h и отсюда находим, что V=40 м/с, т.е. получаем скорость высоты (или высоту скорости), о которой писал Эйлер. А при текущем описании мы описываем весь процесс движения камня между его начальным и конечным положениями и, например, для дифференциального описания при общем решении мы находим решение этого дифференциального уравнения для скорости и пройденного пути, а потом, решая совместно эти два уравнения, находим и нужную скорость. Вообще-то, здесь надо было бы записать закон всемирного тяготения, чтобы найти силу притяжения камня к Земле, но мы, как и при конечном описании, примем, что вблизи поверхности Земли эта сила примерно равна m*g. Тогда аналитическое решение дифференциального уравнения m*d2S/dt2=F=m*g, описывающего движение камня, будет V=g*t и S=h=g*t^2/2. Из последнего уравнения находим t=4 с и из первого V=40 м/с. При этом частное решение этого дифференциального описания, т.е. численными методами, будет подобно решению в приращениях, которое я дам чуть ниже.

 

Или, например, рассмотрим такую задачу. У нас есть шарик массой m привязанный к нитке, пропущенной в отверстие горизонтальной поверхности, и он движется по инерции по окружности вокруг этого отверстия с угловой скоростью w1, а длина нити равна R1. Затем нить потихоньку втягивается в отверстие до тех пор, пока шарик не начнет вращаться по окружности радиуса R2. Следует определить угловую скорость w2. Это очень типичная задача в курсе теоретической механики и решается она там на основании теоремы о сохранении момента количества движения, и, следовательно, здесь должен сохраняться так называемый кинетический момент (7), где J1 и J2 - моменты инерции (J = m*R^2).

 

J1 * w1 = J2 * w2 (7)

 

Но т.к. нас в этой задаче интересуют только начальное и конечное состояния системы, то мы можем ее решить и воспользовавшись законом сохранения энергии. Ведь, если мы посмотрим, а какова стала кинетическая энергия шарика, после того как мы его подтащили, то выясним, что она стала больше и она равна кинетической энергии при вращении по окружности R1 плюс работа, совершенная по подтаскиванию шарика из точки R1 в точку R2 . Решив это уравнение энергетического баланса, приходим к той же зависимости (7), которая и дает ответ для нашей задачи. Но, как и любую другую, эту задачу можно решить и при текущем описание этого процесса в приращениях с использованием всех подходов (импульсного, силового, мощностного и энергетического) или при текущем дифференциальном описании с использованием силового и мощностного подходов. Однако, решение этой конкретной задачи в конечном описании с использованием момента количества движения (импульсный подход) гораздо проще, чем при описании этого процесса с использованием закона сохранения энергии в энергетическом подходе (смотрите [7]) или с использованием текущего дифференциального описания в силовом подходе (смотрите мою программу Konma), поэтому, выбирая метод решения конкретной задачи, надо знать особенности того или иного описания явлений Природы.

 

При этом, как я писал, конечное описание является частным случаем описания явлений Природы в приращениях, т.к. здесь мы просто используем одно большое приращение между начальным и конечным положениями системы. Закон сохранения энергии для конечного описания применим всегда, а вот закон сохранения количества движения не во всех случаях потому, потому что, как я писал в работе [7], количество движения не является полноценной мерой механического движения. Этот закон не применим, когда у нас на систему действуют внешние силы не являющиеся функцией времени, а в Природе все силы являются или функцией перемещений или функцией координат и поэтому получается, что в этом случае закон сохранения количества движения не применим никогда. Но это касается только конечного описания, а при описании явлений Природы в приращениях, когда на малом приращении времени Δt мы можем считать силу постоянной, то всегда можно с использованием закона сохранения количества движения найти и приращение ΔV. Вот, например, в нашем примере с падением камня мы можем считать силу притяжения камня к Земле постоянной на очень больших промежутках времени, т.е. можем считать, что F(t)= F=m*g=const. Поэтому мы здесь можем записать

 

m*(V1+ΔV)-m*V1=F*Δt (8)

 

Т.к. у нас начальная скорость V1 равна нулю, то у нас при первом приращении получится m*ΔV=F*Δt, где в правой части записан, так называемый, импульс силы, который в этой задаче мы можем вычислить. Теперь, если бы у нас задача была сформулирована, как найти скорость через 4 секунды, то мы бы ее нашли, решив задачу через конечное описание

 

ΔV=m*g*Δt/m = 10*4= 40 м/с.

 

А, т.к. нам надо найти скорость, когда высота станет равна нулю, то здесь мы можем найти решение этой задачи с использованием закона сохранения количества движения (импульсного подхода) только в приращениях, т.е., задавая маленькие приращения Δt и вычислять приращения скорости ΔV, а потом по средней скорости на этом отрезке времени Δt вычислять пройденный камнем путь и определять его высоту. Для примера давайте возьмем приращения Δt=1 с и решим эту задачу в приращениях.

 

Δt=1 t=1с ΔV=10 м/с V=10 м/с Vsr=5 м/с S=5 м h=75 м

Δt=1 t=2с ΔV=10 м/с V=20 м/с Vsr=15 м/с S=15 м h=60 м

Δt=1 t=3с ΔV=10 м/с V=30 м/с Vsr=25 м/с S=25 м h=35 м

Δt=1 t=4с ΔV=10 м/с V=40 м/с Vsr=35 м/с S=35 м h= 0 м

 

Здесь у нас, как частный случай, получился точный ответ и при этом шаге решения в приращениях, но обычно при решении задач с такими параметрами объектов надо использовать маленький шаг приращений Δt=0,01 с или еще меньше, чтобы получить ответ с заданной точностью. А вот при описании движения таких объектов, как планеты Солнечной системы, я в программе Solsys решаю дифференциальные уравнения методом Рунге-Кутта с шагом решения (приращением времени) равным 3600 с. Но, если мы рассмотрим задачу удара упругого шара (мяча) в абсолютно жесткую стену, которую я рассматривал в работе [7], то шаг решения надо будет брать, как минимум 0,001 с, т.к. в этом случае у нас при заданных ниже параметрах весь удар будет длиться только 0,03 с. Конкретно там я рассмотрел удар шара массой m= 1 кг и жесткостью C= 10000 Н/м при начальной скорости V1= 10 м/с. Как при этом измененялась скорость его центра масс и сила удара, которая определится как C*X, показано на рис. 0.

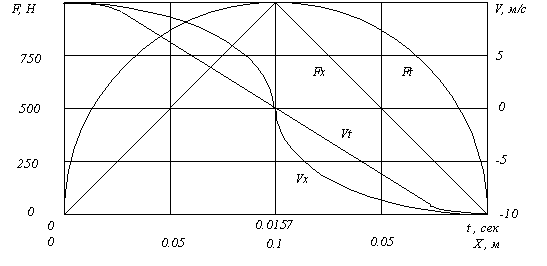
Рис. 0. Зависимости силы удара F и скорости шара V в функции его деформации X и в функции времени t. Воспроизведено из работы [7].

 

При решении этой задачи в работе [7] я использовал для дифференциального описания силовой подход, как частный случай мощностного подхода, но для конечного решения этой задачи удара шара в стену мы вполне можем применить и энергетический подход и можем или по заданной деформации шара найти конечную скорость или по конечной скорости найти получающуюся деформацию. Например, нам надо найти его скорость при деформации X=0,05 м. Записываем энергетический баланс

 

m*V1^2/2=m*V2^2/2+C*X^2/2 (9)

 

и отсюда находим, что скорость V2 будет 8,66 м/с. А вот с импульсным подходом для конечного решения ничего не получится, т.к. здесь мы видим, что сила удара в функции времени явно изменяется, поэтому, чтобы решать эту задачу с использованием импульсного подхода, надо знать эту зависимость, но мы ее можем получить только после аналитического решения этой задачи. Да, в работе [7] я получил такую зависимость F(t) и зависимость для текущей скорости V(t), решив дифференциальное уравнение описывающие процесс удара, поэтому просто для примера я могу определить скорость шара через 0,01 секунды с использованием импульсного подхода. Для этого надо составить импульсный баланс (12), вычислив импульс силы, как интеграл от F(t)*dt на интервале времени от нуля до 0,01 с.

 

F(t)= 1000*sin(100*t) (10)

V(t)= 10*cos(100*t) (11)

m*V1=m*V2+int(F(t)*dt, t=0..0,01) (12)

1*10=1*V2+1000*(1-0,54)/100

 

Отсюда находим V2=5,4 м/с, что соответствует и скорости V(t) найденной по уравнению (11). При этом мы можем проверить это решение и с помощью моей программы Udar3m, где дифференциальное уравнение, описывающее удар двух шаров, решается численными методами (для этой задачи массу и жесткость второго шара надо взять очень большие). При этом данное конечное описание с использованием импульсного подхода имеет только гипотетическую возможность, т.е. его можно осуществить только если уже будет аналитическое решение этой задачи для F(t), но, если такое решение уже есть, то зачем тогда оно нужно это конечное описание с использованием импульсного подхода. Поэтому, в тех случаях, когда у нас внешняя сила, действующая на систему, изменяется во времени по неизвестному закону, то с использованием импульсного подхода возможно только текущее описание системы в приращениях, когда на малом интервале времени Δt можно считать, что сила не изменяется. Естественно, в приращениях возможно и текущее описание с использованием, как энергетического, так и силового и мощностного подходов, а вот дифференциальное описание мы можем получить только при использовании силового или мощностного подходов. При этом как описание в приращениях, так и дифференциальное описание позволяют именно смоделировать описываемые явления Природы и таким образом могут быть использованы и для более детального познания этих явлений Природы.

 

Что касается конечного описания явлений Природы с использованием импульсного и энергетического подходов, то этот вопрос широко освящен в учебниках, и останавливаться на нем я больше не буду. А вот что касается текущего описания, то его я освящу далее очень подробно, т.к. описание в приращениях вообще не освящено в учебниках и данная статья является первой публикацией по данному вопросу, а дифференциальное описание, хоть и дано в учебниках, но дано просто отвратительно, т.к. для этого пытаются притянуть за уши энергетический подход, который здесь совершенно не применим. Для дифференциального описания надо использовать или силовой подход или мощностной, т.к. нам надо описывать мгновенное (текущее) состояние системы в данный момент времени, а импульсный и энергетический подходы позволяют получить только интервальное описание системы в двух разных ее состояниях для двух моментов времени. Начнем подробное рассмотрение описания явлений Природы в приращениях с использованием различных подходов на примере нескольких конкретных задач. Сначала рассмотрим разгон обычной топливной ракеты, а потом рассмотрим разгон безтопливной ракеты, т.е. ракеты у которой масса не изменяется, а двигатель будет ионный и ракеты находятся далеко от других масс. Для этого введем следующие обозначения

 

m1 - масса ракеты до разгона (не изменяется у безтопливной ракеты).

Vgo - cкорость истечения газов или пыли из двигателя на стенде, т.е. относительно ракеты

P - развиваемая двигателем номинальная мощность

V1 - скорость ракеты до разгона

V2 - скорость ракеты в конце разгона.

mg1 - секундный расход топлива (газов или пыли)

mg= mg1*Δt - расход топлива (газа или пыли) за время разгона от скорости V1 до скорости V2

ΔV= V2-V1 - интервал изменения скорости ракеты при разгоне за время Δt

Vsr= (V1+V2)/2= V1+ΔV/2 - средняя скорость ракеты на этапе разгона

Vg= Vgo-Vsr - средняя скорость газов или пыли летящих от ракеты в другую сторону (или летящих вслед за ракетой, если Vgo<Vsr)

Δt - время разгона ракеты от скорости V1 до скорости V2

 

При использовании импульсного и энергетического подходов мы будем находить прирост импульса ракеты или ее энергии на интервале времени Δt, за который ее скорость увеличится на величину ΔV, или время Δt необходимое для увеличения скорости ракеты на величину ΔV. А при использовании силового и мощностного подходов мы будем находить среднюю силу, действующую на элементы системы, или подводимую к ним среднюю мощность на этих интервалах времени или скорости. При этом прирост импульса или энергии будем определять для ракеты, масса которой берется в конце заданных интервалов Δt или ΔV, а среднюю силу и среднюю мощность будем определять для ракеты, масса которой берется в середине интервала Δt или ΔV. При импульсном подходе у нас прирост импульса ракеты будет равен импульсу выброшенных за это время газов (закон сохранения импульса). При силовом подходе у нас средняя сила инерции ракеты будет равна средней силе давления газов на ракету и средней силе инерции массы сгоревшего топлива при торможении этой части топлива от скорости V1 до нуля (второй закон Ньютона в силовой интерпретации Эйлера). При энергетическом подходе у нас прирост энергии ракеты (без массы сгоревшего топлива), равен энергии выработанной двигателем плюс кинетическая энергия сгоревшего топлива, которая перешла к ракете за счет действия сил инерции при торможении этой части топлива от скорости V1 до нуля, и минус энергия улетевших газов. А при мощностном подходе у нас в левой части будет средняя мощность, пошедшая на разгон ракеты, а в правой части будут те же составляющие, что и для энергии, но для средней мощности.

 

(m1-mg1*Δt)*V2 - m1*V1 = mg1*Δt *Vg (13-1) импульсный

 

(m1-mg1*Δt /2)*ΔV/Δt = mg1*Vg + mg1*Vsr = mg1*Vgo (13-2) силовой

 

(m1-mg1*Δt /2)*Vsr*ΔV/Δt = P + mg1*Vsr^2/2 - mg1*Vg^2/2 (13-3) мощностной

 

(m1-mg1*Δt)*(V2^2-V1^2)/2 = P*Δt + mg1*Δt*V1^2/2 - mg1*Δt*Vg^2/2 (13-4) энергетический

 

Отсюда, используя прирост скорости, т.е. задавая V1 и ΔV или V1 и V2 находим время Δt, которое необходимо, чтобы увеличить скорость ракеты от V1 на величину ΔV.

 

Δt = m1 * ΔV / (mg1 * V2 + mg1 * Vg)

импульсный

 

Δt = 2 * m1 * ΔV / (mg1 * ΔV + 2 * mg1 * Vgo)

силовой

 

Δt = 2 * m1 * Vsr * ΔV / (2 * P + mg1 * Vsr * ΔV + mg1 * Vsr ^ 2 - mg1 * Vg ^ 2) мощностной

 

Δt = m1 * (V2 ^ 2 - V1 ^ 2) / (2 * P + mg1 * (V2 ^ 2 - Vg ^ 2)) энергетический

 

Как видим, формулы получились разные, но как я покажу ниже, ответ они дают один и тот же. А теперь давайте перепишем наши формулы импульсного, силового и мощностного балансов так, чтобы можно было по приращению времени Δt находить приращения скорости ΔV. При этом для мощностного баланса я сначала привожу запись, когда не расшифровываю значения Vsr и Vg в приращениях ΔV, т.к. после преобразований правая часть значительно упрощается. Находим из этих трех уравнений выражение для ΔV и видим, что ответ получается один и тот же (14). А для энергетического баланса решение получается неоднозначное, т.к. получается квадратное уравнение, которое имеет два корня и преобразования получаются очень сложные, поэтому я не стал их выполнять вручную и перепоручил это пакету символьных вычислений Maple. Ниже я и привожу получившиеся выражения для двух значений ΔV, но не думаю, что кому-то понравится это решение, которое гораздо сложнее первых трех.

 

(m1-mg1* Δt)*(V1+ΔV) - m1*V1 = mg1*Δt*(Vgo-V1- ΔV/2)

импульсный

 

(m1-mg1*Δt/2)*ΔV/Δt = mg1*Vg + mg1*Vsr = mg1*Vgo

силовой

 

(m1-mg1*Δt/2)*Vsr*ΔV/Δt = mg1*Vgo^2/2 + mg1*(Vsr^2 - (Vgo-Vsr)^2)/2

(m1-mg1*Δt/2)*ΔV/Δt = mg1*Vgo мощностной

 

ΔV = mg1*Δt*Vgo / (m1 - mg1*Δt/2) (14)

 

 

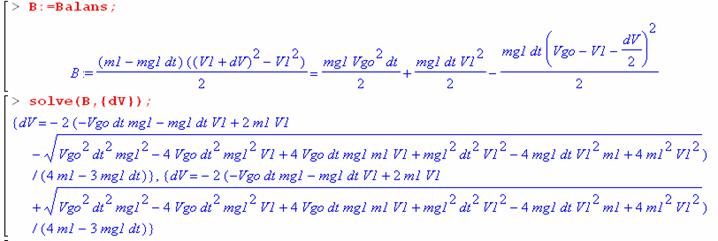
При этом обращаю Ваше внимание, что описание явлений Природы в приращениях хоть и является аналогом дифференциального описания, но не может быть использовано для получения дифференциальных уравнений из этих уравнений в приращениях. Это принципиально разные описания, хотя формально получаются очень похожие формулы. Сравните две нижеприведенных формулы для среднего ускорения (15) и для мгновенного ускорения (16). И даже, если в формуле (15) заменить Δt/2 для ускорения в середине интервала времени на Δt для ускорения в конце этого интервала времени, то все равно это будет не формула (16), а на примере разгона безтопливной ракеты я покажу, что там получаются еще сильнее отличающиеся друг от друга формулы для расчета среднего ускорения и мгновенного. И, чтобы закончить с разгоном топливной ракеты, я приведу и получающиеся при аналитическом решении уравнения (16) формулы для скорости ракеты (17) и пройденного пути (18) в функции времени, а также для времени необходимого для увеличения скорости ракеты на величину ΔV (19). Напоминаю, что формулы для скорости и силы в функции пройденного пути могут существенно отличаться от формул в функции времени и далее на графиках я это продемонстрирую.

 

ΔV/Δt = mg1*Vgo / (m1 - mg1*Δt / 2) (15)

среднее ускорение

 

dV/dt= mg1*Vgo / (m1 - mg1*t) (16)

мгновенное ускорение

 

V(t) = V1 - Vgo * Ln(1 - mg1*t / m1) (17)

S(t) = V1*t + Vgo * ((m1 / mg1 - t) * Ln(1 - mg1*t / m1) + t) (18)

t(ΔV) = m1*(1 - e^(-ΔV/Vgo)) /mg1 (19)

 

А теперь давайте посмотрим, что же у нас получается по приведенным формулам в приращениях и сравним полученные значения с аналитическим решением дифференциального описания. Используя уравнения (13-1)...(13-4) для расчета Δt мы можем задавать начальную скорость V1 и интервал изменения скорости ΔV, т.е. приращение в приемлемых пределах, чтобы задать скорость V2, а потом находить интервал времени Δt1, который необходим, чтобы увеличить скорость V1 на ΔV. А затем мы задаем новую начальную скорость V1+ΔV и конечную V1+2*ΔV и находим Δt2 и т.д. По ходу вычислений мы можем все интервалы Δt суммировать и находить зависимость времени разгона до разной скорости t(V) или в табличном виде или в графическом. А суммируя отрезки пути ΔS=Vsr*Δt находим и зависимость S(V). Хотя, точно также, используя получающиеся данные, можно построить и зависимость V(t) и S(t). А можно задавать начальное время t1 и начальную скорость V1, потом, задавая приращение времени Δt, находить по формуле (14), какое получится приращение скорости ΔV1. Затем задать новое начальное время t1+Δt и новую начальную скорость V1+ΔV1, а потом найти новое приращение скорости ΔV2 на следующем интервале времени Δt и т.д. Точно также, суммируем все получающиеся по ходу вычислений ΔV и находим зависимость V(t) и S(t) или t(V) и S(V).

 

А ниже я привожу данные по времени разгона, которые у меня получаются при разгоне от V1=0 до V2=380 м/с, как по аналитическому решению дифференциального описания (19), так и в приращениях скорости при использовании различных уравнений (13-1)...(13-4), которые у меня получились при различных подходах решения задачи. При этом в расчете использовались данные m1=1000 кг, P=100 кВт, Vgo=200 м/с, а решение в приращениях велось с шагом ΔV=0,001 м/с.

 

t=170,086 276 155 473 - аналитическое решение

t=170,086 276 155 793 - импульсный подход

t=170,086 276 155 793 - силовой подход

t=170,086 276 155 793 - мощностной подход

t=170,086 276 154 408 - энергетический подход

 

Расхождения в последних значащих цифрах, которые дает моя программа (у меня используется 8-и битное представление данных, т.е. получается только 15-ть значащих цифр) объясняется не только наличием шага решения, но и из-за округлений в последней значащей цифре для различных переменных при любом шаге решения, т.к. по ходу вычислений после каждого шага суммируются полученные приращения, то и все эти округления тоже суммируются. Но, как видим, полученная точность решения более чем удовлетворительная и, если не нужна такая высокая точность решения в приращениях, то можно увеличить шаг изменения скорости, что значительно ускорит решение задачи. Такая же хорошая точность решения в приращениях будет и при использовании формулы (14), когда мы будем с шагом Δt=0,001 секунды задавать различные моменты времени и будем находить приращения скорости ΔV. Полученный результат для времени разгона 170 секунд, когда начальная скорость задается равной нулю, мы сравним с аналитическим решением по формуле (17).

 

V=379,423 996 977 176 - аналитическое решение

V=379,423 996 968 305 - решение в приращениях

 

А ниже я привожу графики, получающиеся по найденным зависимостям для аналитического решения и решения в приращениях, которые визуально не отличаются друг от друга, т.к. дают примерно одинаковые результаты. На первых двух графиках развертка идет по Vgo и Vsr, а на нижнем по t. При этом в расчете использовались данные m1=1000 кг, P=100 кВт, Vgo=200 м/с, V1=310 м/с и V2=320 м/с. Если мы строим графики в функции от Vgo или Vsr, то мы на каждом приращении задаем эти значения с заданным шагом от начального (Vn) до конечного значений (Vk) при ΔV=V2-V1=10 м/с. А, если у нас развертка графиков по времени, то мы можем задавать с заданным шагом или приращения скорости ΔV или приращения времени Δt (выбрать в рамке <задать>), а величину приращений задаем в окошке <с шагом>.

 

Рис. 1. Графики изменения времени разгона топливной ракеты t при ее разгоне с 310 до 320 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от изменения скорости газов относительно ракеты. Скриншот программы Raketa9.

 

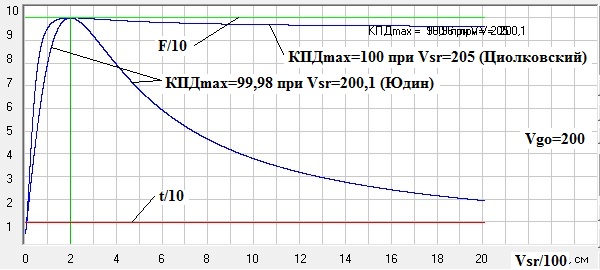
Рис. 2. Графики изменения времени разгона топливной ракеты t при ее разгоне на ΔV=10 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от средней скорости ракеты Vsr, определяемой на интервале ΔV, при скорости газов относительно ракеты Vgo=200 м/с. Скриншот программы Raketa1.

 

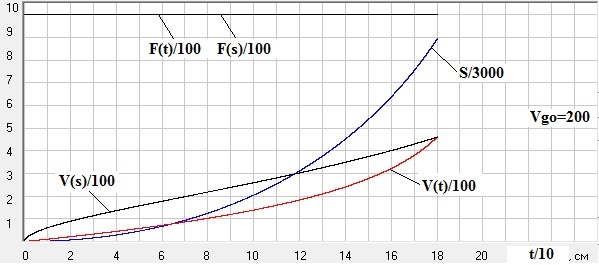
Рис. 3. Графики изменения текущей скорости топливной ракеты V(t) и V(s), пройденного ею пути S(t) и возникающей при этом силы F(t) и F(s), ускоряющей ракету, в функции времени V(t) и F(t) и в функции пройденного пути V(s) и F(s) при скорости газов относительно ракеты Vgo=200 м/с (здесь разгон идет от Vn=0). Скриншот программы Raketa1.

 

Как наглядно видно из этих графиков, КПД движителя ракеты (реактивные двигатели являются одновременно и движителями) имеет для различных режимов разгона строго определенный максимум, который равен 100%. Вот только аналитическое выражение для КПД, полученное Циолковским [24], является ошибочным, т.к. правильно определять КПД движителя надо по формуле (20). Кстати, и вывод аналитической формулы для скорости ракеты, сделанный Циолковским с использованием импульсного подхода [24], является не корректным, хотя сама формула (17), приведенная им, и является правильной. И, исходя из этой формулы, конечная скорость ракеты теоретически ничем не ограничена и при приближении массы ракеты к нулю растет до бесконечности. Поэтому на рис. 3, исходя из технических соображений, приведен график только для скорости ракеты при времени разгона до 180 секунд, т.е. до времени, когда масса ракеты составила 10% от ее начальной массы.

 

КПД=ΔEr / (P*Δt+Eg1) (20)

 

Здесь ΔEr=(m1-mg1*Δt)*V2^2/2 - m1*V1^2/2 - прирост кинетической энергии ракеты без массы сгоревшего топлива, P*Δt - энергия выработанная двигателем за время Δt, а Eg1=mg1*Δt*V1^2/2 - кинетическая энергия топлива, сгоревшего за время Δt

 

А теперь давайте составим балансы в приращениях для разгона безтопливной ракеты. Здесь у нас принципиальным отличием от обычной топливной ракеты будет то, что масса ракеты не будет изменяться, т.к. в качестве топлива мы будем использовать космическую пыль, которую будем собирать по ходу движения ракеты. При этом у нас конструкция пылесборников будет такая, что при разной скорости ракеты в одну секунду будет собираться одно и то же количество пыли mg1. И из пылесборников дозатором в ионный двигатель будет подаваться в одну секунду тоже постоянное количество пыли mg1 для того, чтобы мощность двигателя оставалась постоянной. А энергия на ионизацию пыли и на ее разгон в электрическом поле будет потребляться или от солнечных батарей или от ядерной установки и можно считать, что масса ракеты не изменяется. Давайте, так же, как и для топливной ракеты, составим четыре уравнения балансов при различных подходах. Сначала для задания приращения ΔV и нахождения нужного для этого значения Δt, а потом наоборот.

 

m1*(V2 - V1) = mg1*Δt*Vg (21-1) импульсный

 

m1*ΔV/Δt = mg1*Vg (21-2) силовой

 

m1*Vsr*ΔV/Δt = P - mg1*Vg^2/2 - mg1*Vsr^2/2 (21-3) мощностной

 

m1*(V2^2-V1^2)/2 = P*Δt - mg1*Δt*Vg^2/2 - mg1*Δt*Vsr^2/2 (21-4) энергетический

 

Основным отличием этих уравнений от уравнений (13-1)...(13-4) будет то, что здесь, как это наглядно видно из силового баланса, у нас сила давления газов (ионизорованной пыли) на ракету будет не mg1*Vgo, а mg1*Vg. Это связано с тем, что здесь у нас будет именно та сила давления, которая и должна быть, т.к. теперь у нас в балансе отсутствует сила инерции сгораемого топлива, которая давала дополнительную силу при уменьшении массы топливной ракеты. Хотя, на самом деле, эта сила будет присутствовать, т.к. прежде, чем пыль будет выброшена со скоростью Vgo относительно ракеты, ее скорость также будет уменьшаться от V1 до нуля и масса ракеты будет уменьшаться на величину mg1, но у нас за счет того, что мы ежесекундно в пылесборники будем собирать тоже mg1 кг пыли, масса ракеты уменьшаться не будет. Но у нас появится сила сопротивления движению ракеты, которая в точности будет равна силе инерции возникающей при торможении пыли от V1 до нуля прежде, чем она со скоростью Vgo относительно ракеты будет выброшена из двигателя. Поэтому, в приведенных выше уравнениях должны присутствовать и составляющие, которые я привожу ниже, но, т.к. они взаимно сокращаются, я их не стал записывать.

 

 

- mg1*Δt *Vsr + mg1*Δt*Vsr импульсный

- mg1*Vsr + mg1*Vsr силовой

- mg1*Vsr^2/2 + mg1*Vsr^2/2 мощностной

- mg1*Δt*Vsr^2/2+mg1*Δt*Vsr^2/2 энергетический

 

При этом, как Вы заметили, у нас в мощностном и энергетическом балансах не просто пропали, как в силовом балансе, члены, которые отражали мощность и энергию от действия сил инерции части сгораемого топлива, но и появилась новая составляющая, а именно мощность и энергия, затраченные на нагрев пыли при ее неупругом ударе о пылесборник. А вот, что касается импульсного подхода, то на его балансе изменения во влиянии сил инерции сгораемого топлива никак не отразились, т.к. этот подход для замкнутой системы никак не связан ни с силами, ни с энергиями и является в этом смысле вещью в себе. А, т.к. здесь у нас пыль и рассматривается, как часть системы, но импульс пыли первоначально был равен нулю, то от учета этого нуля здесь нечего и не изменится. Вообще то, считается, что импульсный подход не применим при диссипации энергии, но это справедливо только в том случае, когда диссипация энергии происходит при проскальзывании элементов системы относительно элементов окружающей среды, например, при движении ракеты в сопротивляющейся среде и то при решении задачи в конечном виде, а в приращениях возможно решение и в этом случае. Но эти тонкости импульсного подхода я рассмотрю ниже, а сейчас давайте закончим с разгоном безтопливной ракеты и найдем значения Δt из уравнений (21-1)... (21-4).

 

Δt = m1*ΔV / (mg1*Vg) импульсный

Δt = m1*ΔV / (mg1*Vg) силовой

Δt = 2*m1*ΔV*Vsr / (2*P - mg1*Vsr^2 - mg1*Vg^2) мощностной

Δt = m1*(V2^2 - V1^2) / (2*P - mg1*Vsr^2 - mg1*Vg^2) энергетический

 

Точно так же найдем из уравнений (21-1)... (21-4) и приращеня ΔV в функции от заданного значения Δt. И здесь так же, как и ранее для топливной ракеты, выразим Vsr и Vg через V1 и ΔV. Здесь тоже для расчета ΔV при всех подходах получается одна формула (22), а также и при применении энергетического подхода получается неоднозначное решение и я его не привожу, а для мощностного подхода также привожу вывод с промежуточными выкладками.

 

m1*(V1 + ΔV - V1) = mg1*Δt*(Vgo - V1 - ΔV/2) импульсный

m1*ΔV/Δt = mg1*(Vgo - V1 - ΔV/2) силовой

m1*Vsr*ΔV/Δt = P - mg1*(Vsr^2 - (Vgo-Vsr)^2)/2 мощностной

m1*Vsr*ΔV/Δt = mg1*Vgo*Vsr - mg1*Vsr^2

m1*ΔV/Δt = mg1*Vgo - mg1*(V1+ ΔV/2)

 

ΔV = mg1*Δt*(Vgo - V1) / (m1 + mg1*Δt / 2) (22)

для расчета среднего ускорения

 

ΔV/Δt = mg1*(Vgo - V1) / (m1 + mg1*Δt ) (23)

ускорение в конце приращения

 

dV/dt= mg1*(Vgo-V(t)) / m1 (24)

мгновенное ускорение

 

V(t) = V1 + (Vgo-V1)*(1 - e^(-mg1*t / m1)) (25)

S(t) = Vgo*t + (Vgo-V1)*m1*(e^(-mg1*t /m1) - 1) / mg1 (26)

t(ΔV) = m1*Ln((Vgo-V1) / (Vgo-V2)) / mg1 (27)

 

Здесь так же, как и у топливной ракеты, формула в приращениях для расчета среднего ускорения (22) не подходит для получения дифференциального уравнения, где определяется мгновенное ускорение (24), даже, если мы заменим в формуле (22) Δt/2 для ускорения в середине интервала времени на Δt для ускорения в конце этого интервала времени. Мы видим, что получающаяся при этом формула (23) уже очень заметно отличается от формулы дифференциального описания (24), т.е. это принципиально разные формулы. На особенностях получения дифференциальных уравнений с использованием различных подходов я остановлюсь чуть ниже, а сейчас давайте, так же, как и для топливной ракеты, сравним точность решений в приращениях с данными, получающимися по аналитическим зависимостям, вытекающим из формулы (24). Ниже я привожу данные по времени разгона, которые у меня получаются при разгоне от V1=0 до V2=180 м/с, как по аналитической формуле (27), так и в приращениях скорости при использовании различных уравнений (21-1)...(21-4). При этом в расчете использовались данные m1=1000 кг, P=100 кВт, Vgo=200 м/с, а решение в приращениях велось с шагом ΔV=0,001 м/с.

 

t=460,517 018 598 809 - аналитическое решение

t=460,517 018 578 182 - импульсный подход

t=460,517 018 578 182 - силовой подход

t=460,517 018 578 182 - мощностной подход

t=460,517 018 578 182 - энергетический подход

 

Точно так же хорошая точность решения в приращениях будет и при задании приращений времени и расчета получающихся приращений скорости по формуле (22), когда мы будем с шагом Δt=0,001 с задавать различные моменты времени и будем находить приращения скорости ΔV. Конкретно для времени разгона 460 секунд, когда начальная скорость равна нулю, мы при решении в приращениях и по аналитической формуле (25) получим.

 

V=179,948 231 255 439 - аналитическое решение

V=179,948 231 255 371 - решение в приращениях

 

А сейчас давайте по формулам (21-1)... (21-4) построим графики, чтобы, во-первых, убедиться, что результат по всем формулам получается один и тот же (как видим на рисунках графики совпали) и при этом соответствует расчету по формуле (27) для аналитического решения (и этот график тоже совпал с предыдущими), а во-вторых, чтобы посмотреть как измененяются показатели функционирования безтопливной ракеты при различных режимах ее разгона. На первых двух графиках развертка идет по Vgo и Vsr, а на нижнем по t, но здесь у нас в последнем случае в конце графика получается очень мало точек, т.к. скорость безтопливной ракеты со временем асимптотически приближается к Vgo и поэтому, задавая даже маленькое значение приращения ΔV, мы получаем очень большое приращение Δt. Поэтому, такой график для безтопливной ракеты лучше строить задавая при расчете Δt и находя приращения ΔV по формуле (22). В расчетах, также, как и при разгоне топливной ракеты, начальные данные для расчета были такими m1=1000 кг, P=100 кВт, Vgo=200 м/с, V1=310 м/с и V2=320 м/с. При этом, так же, как и на графиках разгона топливной ракеты, если мы строим графики, например, в функции от Vgo, то мы на каждом приращении задаем эти значения с заданным шагом от начального до конечного заданных значений.

 

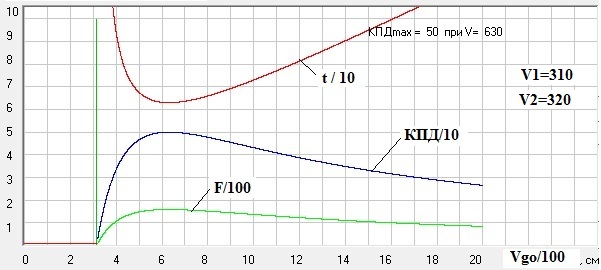
Рис. 4. Графики изменения времени разгона безтопливной ракеты t при ее разгоне с 310 до 320 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от изменения скорости газов относительно ракеты. Скриншот программы Raketa1.

 

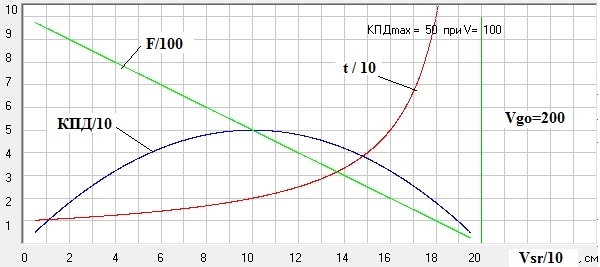
Рис. 5. Графики изменения времени разгона безтопливной ракеты t при ее разгоне на ΔV=10 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от средней скорости ракеты Vsr, определяемой на интервале ΔV, при скорости газов относительно ракеты Vgo=200 м/с. Скриншот программы Raketa1.

 

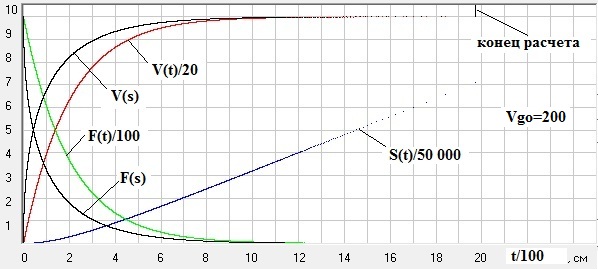
Рис. 6. Графики изменения текущей скорости безтопливной ракеты V(t) и V(s), пройденного ею пути S(t) и возникающей при этом силы F(t) и F(s), ускоряющей ракету, в функции времени V(t) и F(t) и в функции пройденного пути V(s) и F(s) при скорости газов относительно ракеты Vgo=200 м/с (здесь разгон идет от от Vn=0). Скриншот программы Raketa1.

 

Из этих графиков мы так же видим, что КПД движителя ракеты имеет для различных режимов разгона строго определенный максимум и он равен 50%. Это объясняется тем, что теперь у нас кинетическая энергия топлива, сгораемого за время Δt, не передается ракете, т.к. точно такая же знергия затрачивается на разгон этой же массы топлива (пыли) от нуля до скорости ракеты прежде, чем потом эта пыль будет выброшена из ракеты в противоположную сторону, а, кроме того, у нас точно такая же энергия затрачивается еще и на нагрев пыли при ее неупругом столкновении с летящей ракетой. По этому, хотя у нас теперь в формуле (20) энергия Eg1 и равна нулю, но прирост энергии ракеты будет значительно меньше, а конкретно он будет ΔEr=m1*(V2^2-V1^2)/2. И теперь у нас разгон ракеты будет только в том случае, если конечная скорость безтопливной ракеты V2 будет меньше скорости выброса пыли Vgo и при приближении V2 к Vgo прирост скорости ΔV стремится к нулю и, следовательно, скорость ракеты теперь ограничена Vgo. Поэтому на рис. 6, когда мы при расчете в приращениях задавали ΔV и находили Δt, мы видим, что при приближении V2 к Vgo у нас при тех же значениях ΔV получаются все большие и большие значения Δt . А вот, если мы будем задавать приращения Δt и находить приращения ΔV, то мы наоборот получим очень большое количество точек в конце графика при практически одинаковой скорости.

 

Ну, и прежде чем закончить с рассмотрением разгона наших