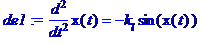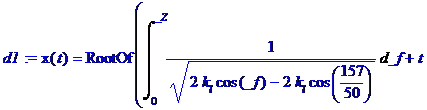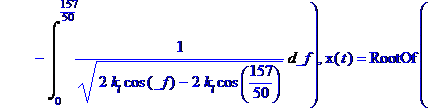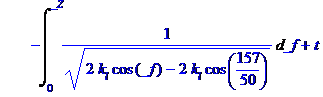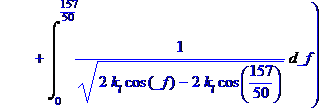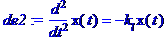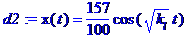Методы решения уравнений математического описания динамических систем

 

Надеюсь, что приведенный мною теоретический материал и конкретные примеры позволят теперь любому желающему корректно и без напряжения описать любые явления Природы и искусственно созданные системы с использованием различных подходов, как в конечном описании, так и в текущем (дифференциальном или в приращениях). И теперь осталось только изложить материал, связанный с решением систем уравнений, описывающих наши системы на языке математики. Что касается различных методов аналитического решения систем дифференциальных уравнений, то останавливаться на этом я почти не буду, т.к. эти вопросы широко освящены в литературе. А вот на численном решении текущего описания систем, как в дифференциальной форме, так и в приращениях я остановлюсь подробно. Исторически сложилось так, что численное решение сложных задач стало возможно только после изобретения компьютеров, а до этого были только разработаны методы численного решения, но решения практически всегда осуществляли аналитическое или геометрическое (если не считать некоторых простейших решений, которые сделал Архимед). Но и сейчас, когда повсеместно используются компьютеры, во всех учебниках рассматриваются только аналитические методы решения задач. Причем студентов упорно убеждают, что аналитическое решение является точным, а численное приближенным, хотя на самом деле все наоборот.

 

Да, существует масса математических задач (повторяю еще раз именно математических), которые решаются аналитически точно, но в Природе таких задач практически нет и получается, что математикам нечего делать в физике. Но им давно уже нечего делать и в математике, поэтому эти математико-физики, т.е. математики, перебравшиеся в физику, стараются как то теоретически обосновать свою нужность в физике. Например, Ландау, чтобы демонстрировать на полных основаниях свои математические познания в физике, во введение к тому Механики 1940 года издания делит всю физику на экспериментальную, теоретическую и математическую. Естественно, он будет заниматься теоретической физикой, а в ней очень важную роль играют приближенные вычисления, которыми он только и занимается, т.е. он будет решать приблизительные задачи с приблизительным решением. Конкретно он пишет

 

«Таким образом приближения играют очень важную роль в общих физических законах. Не менее велика, однако, их роль и при выводе из общих теорий конкретных физических законов. Слишком точные вычисления с учетом несуществующих факторов не только бесплодны и излишне усложняют результаты расчета, но могут даже привести к тому, что существующие в данном явление закономерности вообще выпадут из рассмотрения.»

Здесь, правда, надо заметить, что в издание 1958 года все эти его графоманские рассуждения о трех различных физиках, которые были во введении, додумались все-таки убрать (вместе со всем введением), но вот в последнем издании 2004 года [3] я вдруг обнаружил их опять (правда в приложении и назвали это введение теперь предисловием к первому изданию, но все же вытащили на белый свет, а значит, что это опять кому-то надо).

 

Но я еще раз повторяю, что в Природе таких задач в дифференциальном описании, которые бы решались аналитически точно, практически нет и даже уравнение математического маятника является нелинейным и аналитически не решается. Поэтому математико-физики, чтобы продемонстрировать свою потребность в физике, сначала реальные задачи переводят в условно решаемые, т.е. приблизительные, а потом их решают чаще всего опять таки приблизительными методами. Причем, говоря о приблизительных методах, я не имею в виду, например, итерационные методы решения дифференциальных уравнений, а говорю о различных манипуляциях, которые позволяют сделать не решаемые аналитически дифференциальные уравнения решаемыми. И впервые о фокусах, которые проделываются при аналитическом решении дифференциальных уравнений, я упомянул еще в своей диссертации, где привел пример из учебника по динамике трактора и автомобиля, где авторы в дифференциальном уравнении, которое даже имело аналитическое решение, для простоты его решения просто зачеркнули один член в уравнении и решали оставшуюся часть.

 

А что касается перевода задач в условно решаемые, то здесь сначала отбрасывают массу мелких эффектов, которые затрудняют решение, т.к. считается, что они существенно не повлияют на ответ. Потом, если задача получается не решаемой принципиально, например, получили не линейные дифференциальные уравнения, то ее переводят в решаемую или прямой заменой нелинейных эффектов линейными, например, сухого трения жидкостным или нелинейной жесткости линейной или производят замену нелинейной части уравнения ее приблизительным значением, производя ее разложение в ряд с использованием степенных функций и с отбрасыванием членов высоких порядков и т.д. Так в примере с математическим маятником заменяют sin(φ) на φ, хотя это и приводит к большой ошибке при φ=1,57 рад, т.к. синус при этом получается равен единице. Вот фрагмент моего файла nelinsys22.mws http://modsys/narod.ru/Arhiv/nelinsys22mws.zip для математического пакета Maple, где я рассматриваю аналитическое и численное решение дифференциального уравнения описывающего (моделирующего) движение математического маятника. Кстати, эти же вычисления и для маятника и для кривошипно-шатунного механизма для пакета Maple я нашел и на сайте Экспоненты, поэтому можете скачать похожий файл и оттуда http://exponenta.ru/educat/systemat/chudinov/mech.asp).

 

> restart ;

> # запишем уравнение колебаний маятника приняв k [ l ]:= g / l :

> de1:=diff(x(t),t$2)=-k[l]*sin(x(t));

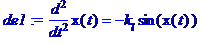
> # как ни странно, но это уравнение не имеет аналитического решения потому что оно не линейное и мы можем в этом убедиться, предложив его решить программе Maple (естественно, выданный ей результат, нас не устраивает)

> d1:=dsolve({de1,x(0)=3.14,D(x)(0)=0},x(t));

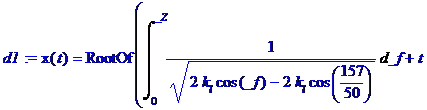
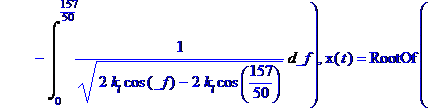
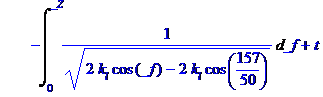
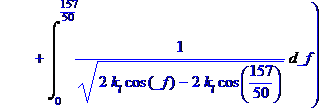
> # но если вместо sin ( x ( t )) написать просто x ( t ), что при малых x будет примерно соответствовать действительности, то такое уравнение будет линейным и его можно решить аналитически

> de2:=diff(x(t),t$2)=-k[l]*x(t);

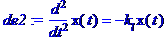
> d2:=dsolve({de2,x(0)=1.57,D(x)(0)=0},x(t));

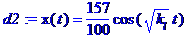
> g:=9.81:l:=1:k[l]:=g/l:

> evalf(d2);

> # теперь по этому уравнению построим график колебаний маятника

> plot(1.57*cos(3.1321*t),t=0..10);

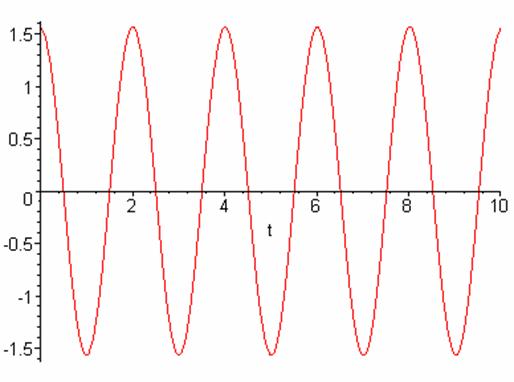
> # а теперь решим численными методами наше исходное уравнение и сравним результат с данными полученными аналитическим методом при подгонке нашего уравнения под линейное

> with(DEtools):

> DEplot(de1,[x(t)],0..10,[[x(0)=1.57,D(x)(0)=0]],stepsize=.01,linecolor=black,arrows=none,thickness=2);

 

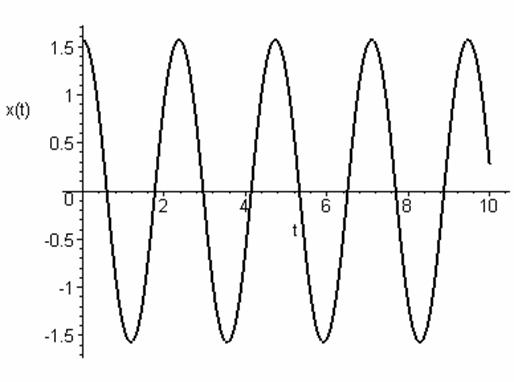
Как видим, при амплитуде колебаний pi/2 у нас получается погрешность в периоде колебаний почти 20%, что является отличным результатом для экономических моделей, но совершенно не допустимо для механических моделей. А, к чему приводит разложение в ряд, я показал на конкретном примере в своей статье [10], который повторю и здесь. Так на стр.47 [4] Ландау пишет

«Для осуществления этого перехода разложим L в ряд по степеням v / c . Тогда, опуская члены высших порядков, получаем: L = - a * c * sqrt (1- v ^2/ c ^2) ≈ - a * c + a * v ^2/(2* c ).»

 

Возьмем для примера a=1, v=290000 км/с, c=300000 км/с и получаем

-a*c*sqrt(1-v^2/c^2) = -76,81

-a*c + a*v^2/(2*c) = -159,83.

Т.е. здесь это приводит к явной ошибке в сотни процентов, но, как я уже писал, Ландау во введении к нулевому изданию своей Механики [1] не только постарался подвести какой то базис под приблизительное решение приблизительных задач, но и пытался доказать, что настоящий ученый только так и должен поступать. А при таких приблизительных методах аналитического решения задач можно получить самые разнообразные ответы, т.е. в зависимости от того, какой ответ нам нужен, мы можем выбрать тот или иной метод приблизительного решения. Показательным в этом плане является пример касающийся уже непосредственно рассматриваемого мною в работе [14] вопроса, о смещении параметров орбит планет. Вот фабула приблизительного аналитического решения по определению смещения перигелия Меркурия выполненного в работе [27].

 

«Как видно из рис. 11.1, при малых βp < 0.3 период траектории φt приближается к единице асимптотически, так что оценить значение φt при таких малых βp, которые присущи Меркурию не возможно. Численное интегрирование уравнений (4.80). (4.82) при таких параметрах дает погрешность, намного превышающую ожидаемое смещение перигелия δφt, в связи с этим рассмотрим приближенное решение уравнения траектории при малых βp. Запишем ……..

 

Так как мы рассматриваем Солнце, то для него Rg<<1, и при малых βt величина A<<1. Поэтому, экспоненту можно разложить в ряд Тейлора….

Разлагая знаменатели слагаемых в правой части и ограничиваясь членами второго порядка, получаем …..

В (11.15) мы ограничивались слагаемыми с показателями степени R меньше 6. Подставляя (11.15) в (4.80), с учетом слагаемых не выше R^3 имеем …..

При β0→0 коэффициенты имеют следующий порядок: F≈1; D≈1; Rg≈1/c1^2; E≈1/c1^4; M≈1/c1^2; N≈h/c1^2;DE≈1/c1^4. Поэтому, пренебрегая слагаемыми с y^3, выражение (11.20) можем проинтегрировать при граничном условии φ(Rp)=0, т.е. угол отсчитывается от перицентрия: …….

Так как гравитационный радиус планет Rg<<Rp, то влияние слагаемых во второй скобке не существенно, поэтому окончательно при βp<<1 вращение перицентрия получаем в виде

 

Δφt = -2*π*a1^2*βp^2 (11.31)

 

Как видим, смещение перицентрия происходит в обратную сторону, т.е. за период частица по орбите проходит угловое расстояние, меньше 2*π. Это противоречит всем полученным нами решениям, в том числе и представленным на рис. 11.1. По абсолютной величине смещение (11.31) превышает значения, рассчитанные численно: (приводится таблица).

Таким образом, полученное приближенное аналитическое решение (11.31) является ошибочным.»

 

Таким образом, у автора этого решения не просто получилась ошибкам в сотню процентов, как мы это видели с примером решения у Ландау, но ответ получился принципиально другим, т.е. получилось отрицательное смещение перигелия. Здесь же надо заметить, что, когда автор писал о больших ошибках численного интегрирования при решении уравнений (4.80) и (4.82), то речь там шла о решении промежуточного решения полученного им же аналитически, поэтому, ошибка-то у него быстрее всего была при аналитическом решении, т.к. при численном интегрировании может быть только небольшая погрешность решения. Причем, что интересно, и при аналитическом выводе им уравнения (4.80) мы встречаем такие же выражения

 

«Это нелинейное дифференциальное уравнение второго порядка. Рассмотрим его решение. С этой целью перейдем к новым переменным …..»

«Таким образом, мы свели (4.68) к нелинейному дифференциальному уравнению первого порядка. Перейдем к новым переменным ….., которые сводят (4.72) к линейному дифференциальному уравнению первого порядка. ….»

 

Т.е. здесь мы видим конкретный пример приведения исходных нелинейных дифференциальных уравнений к линейным. А при решении дифференциальных уравнений численными методами нам все равно какие у нас исходные уравнения (линейные или нелинейные) и сколько и каких эффектов они учитывают. А, как показала моя практика, при их решении на современных компьютерах, например, методом Рунге-Кутта, при правильно подобранных параметрах, ошибка решения обычно не превышает тысячных долей процента. Таким образом, при решении реальных физических задач, а не учебных, надо говорить о том, что численное решение дает почти точный результат, а аналитическое приблизительный. И даже, если разные авторы получили одинаковый результат при приблизительном аналитическом решении приблизительных уравнений, это ни в коей мере не является доказательством того, что будет наблюдаться именно этот эффект. А то вот автор, вышеприведенных длинных цитат, хоть и получил результат с другим знаком, но пытается показать, что его решение не совсем ошибочное и возможно, что это решение Гербера и Эйнштейна ошибочное, а заодно и Сухорукова [28], формулу которого я тоже проверял в своей работе [14]. Кстати, у меня там по формуле Сухорукова получилось при численном решении 8,7294 угл.сек за сто лет, а он согласно своему аналитическому решению по своей формуле (81*) получил 13,99 угл.сек. И я бы не удивился, если бы у Сухорукова получился и совсем другой результат, т.к. все эти аналитические методы решения реальных задач являются приблизительными методами решения приблизительных задач и доверять полученным аналитическим решениям без их проверки численными методами никак нельзя. А в заключении, чтобы Вам стала более понятна вся абсурдность приблизительных аналитических методов решения приблизительных задач и выводов, которые из таких решений делаются, я позволю себе привести еще одну длинную цитату из работы [27]

«Смещение перигелия (11.4), полученное П. Гербером и подтвержденное А. Эйнштейном после подстановки ε, Т и а, согласно (5.14), (5.36) и (5.15), принимает вид

 

Δφt = 6*π*a1^2*βp^2 (11.34)

 

Как видим, полученное нами выражение (11.31) дает в 3 раза меньший по абсолютной величине результат. Г.И. Сухоруков и др. [28] получили тоже в 3 раза меньшее смещение перигелия Меркурия по сравнению с (11.34). Численное значение (11.34) для Меркурия составляет Δφt = 5*10^-7, которое, хотя и в 200 раз больше полученного нами значения 2.7*10^-9, но все же представляет достаточно малую величину. В работе А. Эйнштейна [23] задача двух тел сводится к интегралу (автор приводит выражение 11.35*), который идентичен полученному нами интегралу (11.20). Последний мы решали, ограничиваясь слагаемыми с y^2. А. Эйнштейн интегрировал (11.35) также приближенно, но другим методом. Этим и объясняется отличие результата (11.34) от (11.31). И оба они являются неверными приближенными решениями точного уравнения траектории (4.80)-(4.82).

 

В заключение подведем некоторые итоги:

 

1. Действительная величина прецессии перигелиев планет в настоящее время остается неопределённой.

 

2. Зависимость силы взаимодействия двух тел от скорости приводит к прецессии перицентрия. При очень малых скоростях смещение перицентрия за оборот определяется выражением (11.33), и для Меркурия оно составляет 2.7*10^-9 радиана или 0.23’’ в столетие. Этот эффект представляет такую малую величину, что она никогда не сможет быть подтверждена наблюдениями.

 

3. Величина смещения перигелия Меркурия, определенная У. Леверье на основе закона тяготения Ньютона, подлежит сомнению и для его нахождения должна быть решена «проблема многих тел».

 

Теперь давайте подведём уже итоги по итогам, которые сделал математико-физик Смульский. Здесь мы с одной стороны видим явное утверждение о том, что все аналитические методы решения являются приближёнными и могут давать совершенно разные результаты, а с другой стороны, мы видим слепую веру в безупречность полученного им аналитического решения (4.80*). И даже расчетные данные Гербера и Эйнштейна, хоть они и отличаются от полученных им данных, он ставит выше наблюдаемых данных. Более того, Смульский утверждает, что раз данные наблюдений не подтверждают его теорию, то ошибочными являются именно данные наблюдений. Правда, он оставляет нам маленькую возможность возразить ему, если мы решим проблему многих тел и подтвердим величину смещения перигелия Меркурия определенную Леверье. И я как раз решил эту проблему почти точными методами численного решения дифференциальных уравнений и доказал справедливость данных Леверье [13], так что эти выводы математико-физика Смульского о справедливости его теории ошибочны. А вот его вывод о том, что «Этот эффект представляет такую малую величину, что она никогда не сможет быть подтверждена наблюдениями», уже явно не является выводом о точности аналитических решений и попахивает позитивизмом и явным утверждением о том, что мир непознаваем. И тут Смульский оправдывает философские взгляды других математико-физиков, которые отрицают познаваемость микромира и утверждают, что мы можем только статистическими распределениями описать в современной квантовой механике видимые нами эффекты от процессов, протекающих в микромире. И делают они так не потому, что имеют какие-то философские взгляды на вопросы микромира, а потому, что они, во-первых, не могут грамотно описать эти процессы, а во-вторых, принципиально не могут решить эту задачу аналитически, т.к. уже в атоме гелия мы имеем ядро и два электрона, то есть уже задачу трёх тел.

 

Таким образом, вся научная философия математико-физиков сводится не к изучению внутренних пружин заставляющих протекать процессы так или иначе, а к изобретению различных математических выражений, которые бы удовлетворительно описывали наблюдаемые нами эффекты. При этом закрываются глаза на любые несуразности и ошибки, если полученная формула позволяет это сделать, например, как мы это видели у Планка [9] при выводе им своей формулы. Или возьмем ОТО Эйнштейна, где считается, что скорость распространения гравитации равна скорости света, но все решения с применением этой теории, которые приводятся в учебниках, получены аналитическим путем, а сделать это не возможно при учете скорости гравитации для расчета запаздывания по координатам. Таким образом, и в ОТО, также как и у Гербера, фактически принята скорость гравитации равная бесконечности. Да у них и уравнение для расчета аномального смещения перигелия Меркурия получилось одно и то же. При чем, что интересно, свои уравнения гравитационного поля Эйнштейн получил уже после того, как опубликовал эту формулу [23], т.е. получается, что он просто передрал эту формулу у Гербера, а потом подгонял свои уравнения поля под нее. Хотя здесь не всё так однозначно, т.к. само решение общековариантного тензорного уравнения Эйнштейн украл у математика Гильберта, а тот уж точно ничего не подгонял под заданный ответ.

 

Вообще-то, примерно то же самое, т.е. подгонку своего решения задачи под заданный ответ (пусть даже и несознательно) делали все математико-физики и в то время делают и сейчас, т.к. они пытались и пытаются объяснить своими физическими теориями, например, именно аномальное смещение перигелия Меркурия, а не физическое явление гравитации. И хотя, нужный практический результат давала и просто поправка Холла к закону тяготения, но эти якобы ученые пытались получить нужный результат именно путем видоизменения закона тяготения исходя из каких-то теоретических предпосылок. А теории должны не заранее подгоняться под нужный результат, а создаваться исходя из существующих представлений об окружающем мире, а потом уже проверяться по получающимся результатам. Вообще-то за такие вещи, когда теория подгоняется под нужный результат, надо не Нобелевские премии давать, как, например, Планку и Эйнштейну или Тейлору и Халсу, а наказывать. Вопрос только в том, кто и как будет наказывать. При этом я не призываю казнить таких мошенников, как раньше казнили еретиков, а по подсчетам Вольтера таковых набралось 9 718 800 человек, но что-то надо делать, т.к. наука за последние 100 лет деградировала и многие достижения техники сделаны инженерами не благодаря таким теориям, как квантовая механика или ОТО, а вопреки им.

 

В общем, мне кажется, что процесс оболванивания в науке достиг своего апогея. И, если при работе над своей статьёй [10], я еще удивлялся, как все эти математико-физики не видят явных ляпов в применении принципа наименьшего действия у Ландау и Фейнмана, то сейчас я уже не знаю чему удивляться. И во многом этому оболваниванию способствует то, что и сейчас продолжают упорно учить студентов только аналитическим методам решения задач, а, т.к. реальные задачи не решаются аналитически, то выдумываются любые самые фантастические теории, где критерием их истинности является только то, что с использованием этих теорий решение задач можно получить аналитически. Т.е. во главу угла здесь ставится не физическая сущность рассматриваемых явлений Природы, а только требования математики к этим теориям. А чтобы повернуть процесс развития науки в правильное русло, надо больше учить студентов именно численным методам решения задач, а не аналитическим, т.к. сложность решаемых сегодня задач возросла настолько, что аналитически они уже не решаются.

 

А вот если мы опишем явления Природы в приращениях и будем потом по этому описанию решать эту задачу численным методом, то никаких проблем у нас не возникает. Точно также не будет никаких проблем ни с задачей трех тел, ни с нелинейностью дифференциальных уравнений, если мы будем решать систему дифференциальных уравнений, описывающих явление Природы или искусственную систему численными методами. При этом простейшим методом численного решения дифференциальных уравнений является метод Эйлера, согласно которому по заданным в данный момент времени T1 координатам тел и их скоростям находятся силы, действующие на эти тела, а потом, согласно 2-у закону Ньютона в интерпретации Эйлера, т.е. уже в современной трактовке, находятся ускорения масс при действии на них, полученных сил. Затем, по найденным ускорениям, уточняются скорости тел и из предположения, что за очень маленький промежуток времени P0 они изменяться незначительно, делается расчет новых скоростей и новых координат тел в новый момент времени T1+P0 и т.д.

 

Но метод Эйлера очень неточен при большой кривизне траектории движения, и особенно, если мы имеем знакопеременную функцию, поэтому накапливается большая ошибка при увеличении времени решения задачи. Этих недостатков практически лишен метод Рунге-Кутта по 4-м коэффициентам, где у нас 4-е раза как бы прощупывается кривизна траектории для разных моментов времени, а потом делается окончательный расчет новых координат и скоростей для следующего момента времени T1+P0 с учетом полученных 4-х промежуточных значений координат и скоростей, рассчитанных для моментов времени T1, T1+P0/2 (два раза) и T1+P0. А при описании в приращениях у нас, как и в методе Эйлера, на одном шаге решения P0 (шаге приращения) делается только одно вычисление новых параметров системы, но точность решения получается гораздо выше. Наглядно точность этих двух методов отражает рисунок 13, где приведена зависимость высоты подъема камня в функции времени h(t). Но, допустим у нас нет этого аналитического решения, а есть только дифференциальное уравнение dh/dt=f(h,t) и нам надо его решить методом Эйлера, чтобы получить график зависимости h(t). В момент времени T1 скорость подъема dh/dt будет равна тангенсу угла наклона кривой h(t), т.е. тангенсу угла Q1e. Поэтому за шаг времени P0 у нас камень должен подняться на высоту h1e. На следующем шаге решения в момент времени T1+P0 касательная к функции h(t) будет проходить под углом Q2e, поэтому из этой точки проводим отрезок прямой под этим углом до момента времени T1+2P0 и получаем высоту h2e и т.д.

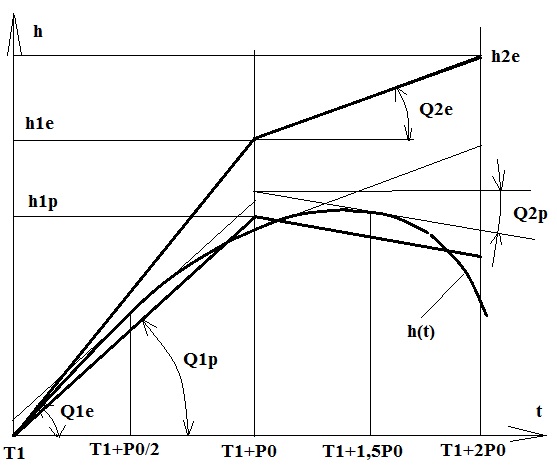
Рис. 13. Сравнительная схема численного решения в приращениях и методом Эйлера.

 

А при описании в приращениях у нас находится среднее приращение скорости на шаге решения, т.е. можно сказать, что мы находим производную в точке T1+P0/2, но при условии, что кривизна поверхности на этом шаге не изменяется, и потом мы вычисляем и среднюю скорость, что более точно отражает производную dh/dtна этом шаге решения. А далее мы точно также из точки T1 проводим прямую, но под углом Q1p и находим высоту в конце этого шага решения h1p. А потом уже из этой точки на следующем шаге решения проводим прямую под углом Q2p и т.д. Как мы уже видели выше, при решении задачи разгона топливной ракеты в приращениях у нас при шаге решения Δt= P0=0,001 секунды решение в приращениях дает очень хорошую точность. А сейчас давайте сравним ее с точностью численного решения дифференциального уравнения описывающего разгон топливной ракеты методами Эйлера и Рунге-Кутта с этим же шагом, т.е. тоже определим скорость ракеты через 170 секунд.

 

V=379,423 996 977 176 - аналитическое решение

V=379,423 996 968 305 - решение в приращениях с P0=0,001

V=379,423 996 977 281 - решение в приращениях с P0=0,00025

V=379,423 996 978 800 - метод Рунге-Кутта с P0=0,001

V=379,421 163 663 565 - метод Эйлера с P0=0,001

 

Как видим, метод Эйлера действительно дает большую погрешность даже при незначительной кривизне функции скорости и таком маленьком шаге решения, а метод Рунге-Кутта дает отличный результат, т.к. точность решения даже на одну значащую цифру лучше, чем при решении в приращениях. Но при одинаковом времени решения, т.е., когда шаг решения в приращениях в 4 раза меньше, чем при решении методом Рунге-Кутта, точность решения в приращениях может быть даже выше. Но все это было в том случае, когда функция скорости не меняла знака, поэтому давайте посмотрим, как эти методы покажут себя при знакопеременной функции. Пусть у нас на тело массой m1 действует сила, которая изменяется по закону F = Fo*cos(w*T), где w- круговая частота, T- текущее время, а Fo- максимальное значение силы, которое в программе Raketa будем задавать как Fo= mg1*Vgo. Таким образом, для всех ниже рассмотренных примеров у нас при тех исходных данных, что мы задавали, рассматривая разгон топливной и безтопливной ракет, Fo будет 5*200=1000 Н, а m1 будет 1000 кг.

 

Давайте вычислим, какова будет скорость тела массой m1 при круговой частоте изменения силы w = 0,5 рад/с. Дифференциальное уравнение, которое будет описывать движение массы, у нас будет (44). У него есть аналитическое решение и оно для скорости массы в момент времени T будет (45), а для пути пройденного этой массой (46), где V1 это начальная скорость массы, т.е. в момент времени T=0. А, если мы опишем движение этой массы в приращениях, то мы получим уравнения (47) и (48), где V1 это скорость в начале шага решения P0, т.е. в момент времени T1, а V2 это скорость в конце шага решения (шага приращения времени), т.е. в момент времени T2=T1+P0, и то же самое для S1 и S2. Чтобы наглядно были видны погрешности решения, возможные при численном решении, давайте сравним аналитическое решение с численным решением методом Эйлера, которые даны на рис.14.

 

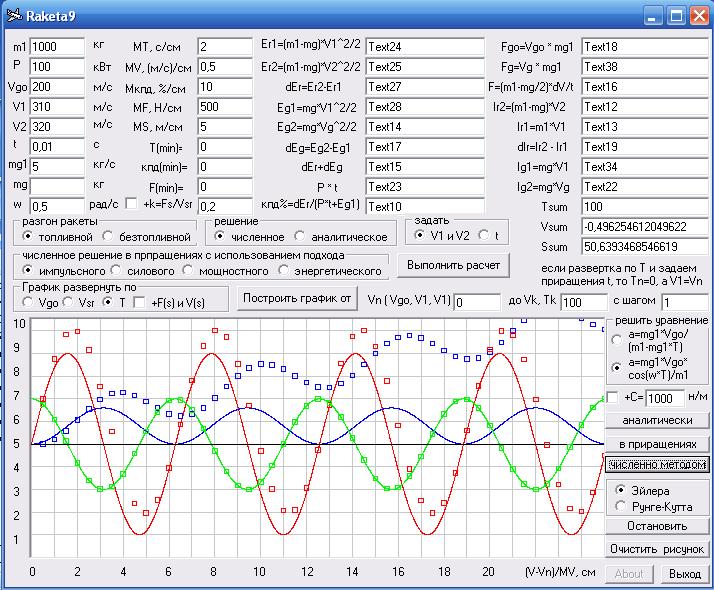
Рис.14. Сравнение точности решения задачи при воздействии на массу периодической силы. Сплошные линии – аналитическое решение дифференциального описания (44) и квадратики – численное решение методом Эйлера с шагом 1 с. Зеленые точки – сила, красные – скорость и синие – смещение тела в функции времени. Скриншот программы Raketa9.

 

m1*dV/dt=Fo*cos(w*T) (44)

V = V1 + Fo*sin(w*T) / (m1*w) (45)

S = V1*T + Fo* (1 - cos(w*T)) / (m1*w^2) (46)

V2 = V1 + ΔV= V1 + P0*Fo* cos(w*(T1+P0/2)) / m1 (47)

S2 = S1 + P0 * (V1+V2)/2 (48)

 

Здесь мы явно видим, что метод Эйлера для решения таких задач не подходит, т.к. у него идет постоянное запаздывание по используемой в расчетах скорости, что наглядно было видно и на рис. 13, в результате мы имеем камулятивное накопление ошибки по смещению. А вот метод Рунге-Кутта для дифференциального описания и описание в приращениях, как мы это видим на рис. 15, прекрасно справляются с этой задачей при том же шаге решения 1 с. Здесь у нас на графиках скорости и перемещеня при решении описания в приращениях (кружки) совпали с решением дифференциального описания методом Рунге-Кутта (квадратики) и хорошо легли на линии аналитического решения. А вот на графике силы мы видим, что кружки и квадратики не совпали друг с другом, хотя и те и те хорошо легли на линию аналитического решения. Это объясняется тем, что при численном решении дифференциального уравнения сила вычислялась четыре раза и я вывел на график ее значение для времени в конце шага решения, как и для скоростей и перемещений, а при решении задачи в приращениях нам нужна была сила на середине шага решения, где я ее и вычислял, поэтому и на график я вывел ее значение для этого момента времени.

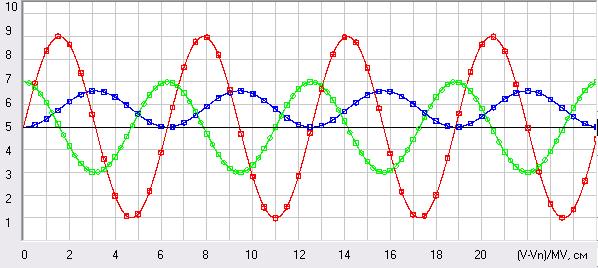
Рис. 15. Решение задачи при воздействии на массу периодической силы. Сплошные линии – аналитическое решение дифференциального описания (44), квадратики – его численное решение методом Рунге-Кутта с шагом P0=1 с и кружки - описание (оно же и решение) в приращениях (47) и (48) с шагом P0=1 с. Скриншот программы Raketa1.

 

Но самым жестким тестом на точность решения задачи тем или иным методом является режим резонанса в системах, поэтому давайте рассмотрим и систему, где на массу будет действовать не только внешняя периодическая сила, но и внутренняя сила возникающая в пружине жесткостью С, с которой соединена наша масса. Дифференциальное описание данной системы будет (49). Это уравнение тоже имеет аналитическое решение для скорости (50) и отклонения от положения равновесия системы (51). А, если у нас начальная скорость V1=0, то получатся более простые формулы (50') и (51'), где k = (C / m1)^0,5 это собственная частота колебаний этой системы. А описание данной системы в приращениях (оно же решение) будет (52) и (53), где V1 это скорость в начале шага решения P0, т.е. в момент времени T1, а V2 это скорость в конце шага решения (шага приращения времени), т.е. в момент времени T2=T1+P0, и то же самое для S1 и S2.

 

m1*dV/dt = -C * S + Fo*cos(w*T)  

               (49)

V = V1*k*(m1 / C)^0,5*cos(k* T) + Fo*(k*sin(k*T) - w*sin(w*T)) / (C – m1*w^2)

                            (50)

S = V1*(m1 / C)^0,5*sin(k*T) - Fo*(cos(k*T) - cos(w*T)) / (C – m1*w^2)

                (51)

V = Fo*(k*sin(k* T) - w*sin(w*T)) / (C – m1*w^2)                         (50’)

S = Fo*(cos(w*T) - cos(k* T)) / (C – m1*w^2)   

                           (51’)

V2=V1 + ΔV= V1 + P0*(Fo*cos(w*(T1+P0/2)) - C*S1) / (m1 + C*P0^2 / 2)  

                        (52)

S2=S1 + P0*(V1+V2)/2 (53)

 

К сожалению, аналитическое решение уравнения (49) не имеет, так сказать, решения потому, что в знаменателе формул (50) и (51) получается ноль, а делить на ноль нельзя. А получается это потому, что при резонансе у нас частота вынужденных колебаний должна совпадать с частотой собственных колебаний системы, т.е. w должно быть равно k=(C/m1)^0,5. И, если мы подставим это значение w в формулы (50) и (51), то у нас в знаменателе получится C-C. А при численном решении уравнения (49) никаких проблем не возникает. Их не будет и при описании этого процесса в приращениях. Смотрите рис. 16 при жесткости С=1000 Н/м и частоте w=1 рад/с. Там все графики практически совпадают, но все же имеется маленькое отличие. Вот только не понятно какое решение более точное – дифференциального описания (49) методом Рунге-Кутта или решение в приращениях (52) и (53).

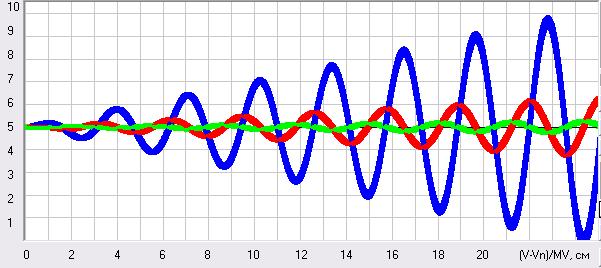
Рис. 16. Режим резонанса при решении дифференциального описания (49) методом Рунге-Кутта и решении задачи в приращениях (52) и (53) при шаге решения (приращения) 0,01 с. Масштабы были следующие MT=2 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

Выяснить мы это сможем, если рассмотрим режим биений, т.е. режим близкий к резонансному, когда частота вынужденных колебаний немного отличается от частоты собственных колебаний системы. Кстати, если мы зададим частоту вынужденных колебаний w=0,999*k, то мы получим по формулам аналитического решения в начале процесса резонанса почти точное решение для режима резонанса, но мы возьмем эту частоту такой, чтобы у нас в обозримом времени явно просматривалось несколько циклов биений. Пусть у нас жесткость так и останется 1000 Н/м, т.е. частота собственных колебаний так и будет 1 рад/с, а частоту вынужденных колебаний зададим 0,95 рад/с. Биения в системе, возникающие при таких параметрах вы видите на ниже приведенных рисунках 17, 18 и 19, где тонкие сплошные линии это аналитическое решение дифференциального описания системы (49), а толстые линии, в которые слились квадратики и кружки, это решение этого описания методом Рунге-Кутта и решение описания в приращениях. Как видим, на рис. 17 у нас оба решения практически слились, т.е., если погрешность численного решения методом Рунге-Кутта и есть, то она даже при шаге решения 0,01 с очень маленькая. А вот решение в приращениях с таким шагом дает очень большую погрешность (рис. 18), но может быть она станет такой же при шаге решения 0,0025 с, когда время решения этой задачи на компьютере методом Рунге-Кутта и в приращениях будет примерно одно и то же и тогда можно будет говорить о равнозначности точности этих решений. Ответ на этот вопрос дают графики на рис. 19.

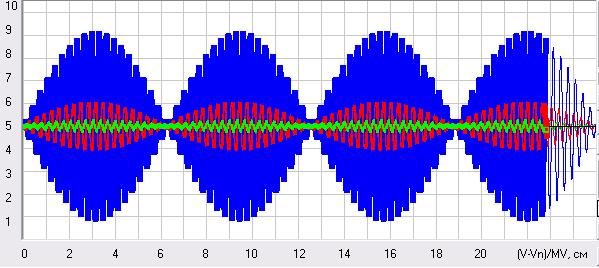
Рис. 17. Режим биений при решении дифференциального описания (49) методом Рунге-Кутта при шаге решения 0,01 с. Масштабы были следующие MT=20 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

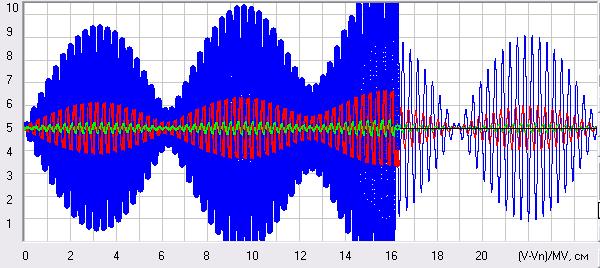
Рис. 18. Режим биений при решении задачи в приращениях (52) и (53) при шаге решения (приращения) 0,01 с. Масштабы были следующие MT=20 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

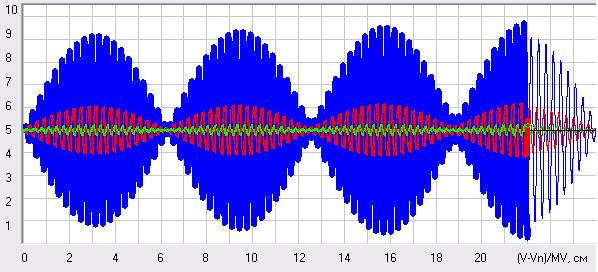
Рис. 19. Режим биений при решении задачи в приращениях (52) и (53) при шаге решения (приращения) 0,0025 с. Масштабы были следующие MT=20 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

 

Как видим, решение в приращениях даже при шаге решения 0,0025 с, хоть и стало гораздо лучше, чем при шаге решения 0,01 с, но все равно гораздо хуже, чем при решении методом Рунге-Кутта при шаге решения 0,01 с. Таким образом, в общем случае описание систем в приращениях при том же времени решения задачи на компьютере не может соперничать по точности решения с решением дифференциального описания методом Рунге-Кутта. Хотя, например, для экономических систем описание в приращениях и является единственно возможным описанием, т.к. хотя, как я отмечал в работе [6], в этих системах и наблюдаются инерционные свойства систем, как и в механических системах, но дифференциальное описание ускорений для процессов в этих системах получить не удается. Поэтому описание явлений Природы и искусственных систем в приращениях все же может в некоторых случаях соперничать с дифференциальным описанием и последующим решением этого описания методом Рунге-Кутта. Я здесь ничего не говорю о преимуществах аналитического решения для дифференциального описания, т.к. для реальных систем, а не для учебных, получается такое дифференциальное описание, которое никогда не имеет аналитического решения.

 

А сейчас давайте немного остановимся на допустимых погрешностях численного решения задач, т.к. мы чаще всего не можем даже оценить эту погрешность из-за того, что при решении реальных задач у нас полученный ответ просто не с чем сравнить, т.к. у нас нет аналитического решения. Да, здесь чем меньше шаг решения и чем выше разрядность представления данных, которую может обеспечить наша операционная система на компьютере и используемый язык программирования, тем будет меньше погрешность решения из-за округления данных в последней значащей цифре, которая будет кумулятивно накапливаться. Но вместе с тем у нас, чем меньше шаг решения, тем больше будет время работы компьютера при решении нашей задачи, поэтому погрешность численного решения всегда должна определяться компромиссно со временем решения задачи. Например, для оптимизации абсолютной скорости Солнечной системы и скорости гравитации мне надо на математической динамической механической модели Солнечной системы проводить десятки вычислительных экспериментов по планам многофакторного планирования. И для 6-и факторного рототабельного плана мне надо провести 79 экспериментов, каждый из которых для определения, например, параметров орбиты Меркурия длится около 7 часов. Итого на весь план требуется 553 часа, т.е. при непрерывной работе компьютера это будет 23 дня. А, если учесть, что мне надо выполнить десятки таких планов, то время работы компьютера измеряется уже годами. И это не считая времени для составления этих планов и обработки данных вычислительных экспериментов.

 

Да, сейчас я использую четырехядерный компьютер и это позволяет сократить время его работы почти в четыре раза, т.к. я запускаю программу Solsys7mm