Рассмотрим случай сеточной функции, определенной на равномерной сетке
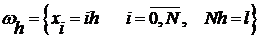 ,
, 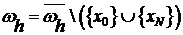 .
.
Будем рассматривать финитные сеточные функции, если:
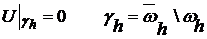 .
.
Содержательно, факт финитности означает, что в случае граничных условий первого рода разностную задачу можно переформулировать таким образом, что граничные условия станут нулевыми.
(1)  ;
;
(2)  ;
;
Пусть 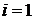
(3) 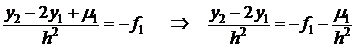 .
.
Аналогично для 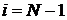
(4)  .
.
Будем считать, что  .
.
Изменим постановку задачи (1), (2), скорректировав правую часть в зависимости от узла (в приграничных узлах), а также заменив правые условия на однородные.
(5)  ;
;
(6)  ;
;
(7) 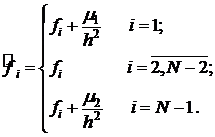
Задачи (1), (2) и (5), (6) эквивалентны за исключением двух точек: х=0, х=N-1, где значения сеточных функций были переопределены.
Введем на сетке  скалярное произведение:
скалярное произведение: 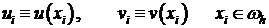 .
.
(8) 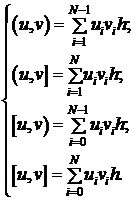
___________________________________________________________
‼ Проверить аксиомы скалярного произведения самостоятельно.
___________________________________________________________
На пространстве сеточных функций определенных на сетке  рассмотрим оператор симметричной разностной производной второго порядка
рассмотрим оператор симметричной разностной производной второго порядка 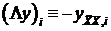 .
.
 .
.
Используя ранее введенные формулы Грина, установим некоторые свойства этого оператора.
Свойство 1.
Оператор  является положительным, т.е.
является положительным, т.е. 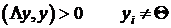 ,
, 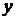 из пространства финитных функций из гильбертова пространства, т.е.
из пространства финитных функций из гильбертова пространства, т.е. 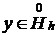 .
.
Доказательство:
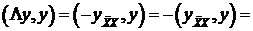
Используем первую формулу Грина, где 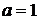 ,
, 
 .
.
В соответствии с полученными результатами задача (1), (2) сведенная к задаче (5), (6) имеет единственное решение. Это следует из того факта, что задача (5), (6) может быть записана в виде 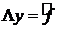 , где
, где 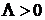 , следовательно, существует и ограничен оператор
, следовательно, существует и ограничен оператор  , таким образом
, таким образом  . Кроме того,
. Кроме того, 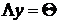 тогда и только тогда, когда
тогда и только тогда, когда 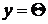 .
.
___________________________________________________________
‼ Показать самостоятельно, что этот оператор линейный.
___________________________________________________________
Свойство 2.
Оператор  является самосопряженным, т.е.
является самосопряженным, т.е. 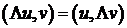 ,.
,.
Доказательство:
Используем вторую разностную формулу Грина,

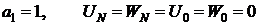 .
.
Следовательно,  .
.
Второе свойство в совокупности с первым позволяет ввести энергетическое пространство сеточных функций, которое представляет собой частный случай Гильбертова пространства сеточных функций с определенным специальным образом скалярным произведением и нормы, которая называется энергетической нормой.
 .
.
________________________________________________________________
‼ Доказать, что введенное таким образом скалярное произведение удовлетворяет всем аксиомам скалярного произведения. Показать самостоятельно, что этот оператор линейный. Проследить где используется самосопряженность оператора, а где его положительность.
________________________________________________________________
(9) 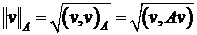 ;
;
(10) 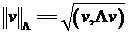 .
.
Получим нужные в дальнейшем оценки вида:
(11) 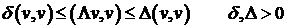 .
.
Эти оценки, по возможности, должны быть не улучшаемыми, т.е.  должно быть наименьшим, а
должно быть наименьшим, а  - наибольшей константами.
- наибольшей константами.
Получим оценку (11) используя информацию о спектре оператора  .
.
___________________________________________________________________________________________________________
‼ Доказать равенство самостоятельно.
________________________________________________________________
Ранее было получено, что спектральная задача:
 ;
;

имеет решение:
(12)  - собственные значения.
- собственные значения.
(13) 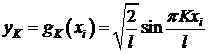 ;
;
(14)  ,
, 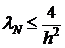 .
.
Так как оператор  самосопряженный, то существует базис из собственных векторов этого оператора, который можно пронормировать. Элементы этого базиса заданы собственными функциями
самосопряженный, то существует базис из собственных векторов этого оператора, который можно пронормировать. Элементы этого базиса заданы собственными функциями 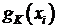 .
.

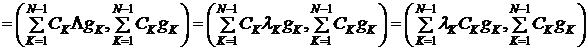
в силу ортогональности
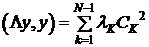 .(15)
.(15)
Оценим сверху и снизу полученную сумму.
 .
.
Учитывая равенство (15) и последнее соотношение, получаем:
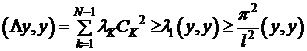 .
.
В виде  можно взять
можно взять 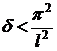 . На самом деле, приведенное ранее значение
. На самом деле, приведенное ранее значение 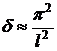 превышает
превышает 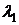 , т.к.
, т.к. 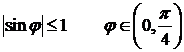 . Поэтому
. Поэтому  должна быть заменена на
должна быть заменена на  .
.
Используя (15), получим оценку сверху.
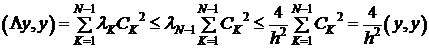 .
.
Итак, получили оценку:
(16) 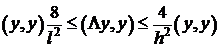 .
.
Вспомним определение нормы оператора в линейном нормированном пространстве.
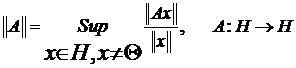 .
.
Не трудно показать, что
(17)  .
.
В этой оценке понимается минимальная из всех возможных норм оператора.
________________________________________________________________
‼ Показать самостоятельно, что  с точностью до величины О(1).
с точностью до величины О(1).
________________________________________________________________





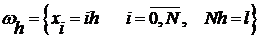 ,
, 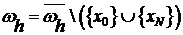 .
.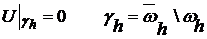 .
. ;
; ;
;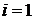
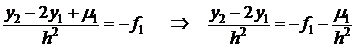 .
.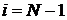
 .
. .
. ;
;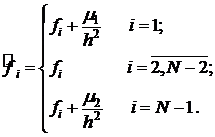
 скалярное произведение:
скалярное произведение: 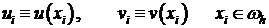 .
.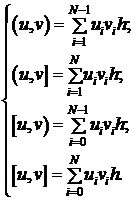
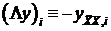 .
. .
. является положительным, т.е.
является положительным, т.е. 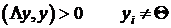 ,
, 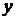 из пространства финитных функций из гильбертова пространства, т.е.
из пространства финитных функций из гильбертова пространства, т.е. 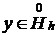 .
.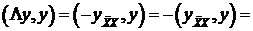
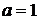 ,
, 
 .
.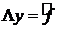 , где
, где 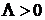 , следовательно, существует и ограничен оператор
, следовательно, существует и ограничен оператор  , таким образом
, таким образом  . Кроме того,
. Кроме того, 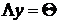 тогда и только тогда, когда
тогда и только тогда, когда 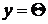 .
.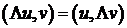 ,.
,.
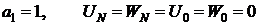 .
. .
. .
.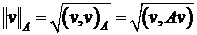 ;
;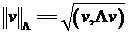 .
.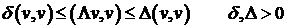 .
. должно быть наименьшим, а
должно быть наименьшим, а  - наибольшей константами.
- наибольшей константами. ;
;
 - собственные значения.
- собственные значения.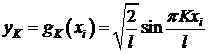 ;
; ,
, 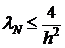 .
.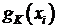 .
.
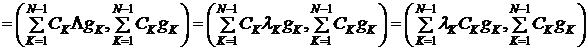
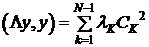 .(15)
.(15) .
.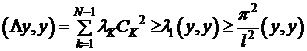 .
.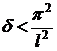 . На самом деле, приведенное ранее значение
. На самом деле, приведенное ранее значение 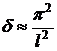 превышает
превышает 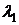 , т.к.
, т.к. 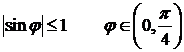 . Поэтому
. Поэтому  .
.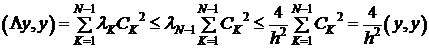 .
.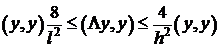 .
.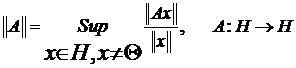 .
. .
.


