До сих пор мы рассматривали простейшие операторы, не зависящие от пространственных переменных. На практике это редко встречающаяся ситуация. Поэтому получим оценки для оператора разностной производной второго порядка с переменными коэффициентами.
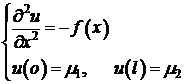
 ;
;
 .
.
В двумерном случае рассматривается задача Дирихле.
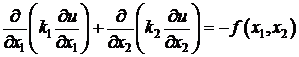 ;
;
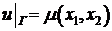 ,
,
В этих задачах мы приходим к оператору второго порядка с переменными коэффициентами.
(1) 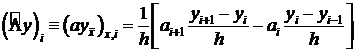 .
.
Будем использовать:
(2) 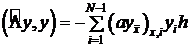 .
.
Получим по возможности более точные оценки вида:
(3) 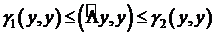 , где константы
, где константы  и не могут быть улучшены.
и не могут быть улучшены.
Опр. 1
Постоянные 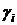 в неравенстве (3) называются постоянными энергетической эквивалентности или энергетическими постоянными.
в неравенстве (3) называются постоянными энергетической эквивалентности или энергетическими постоянными.
Воспользуемся первой разностной формулой Грина для финитных сеточных функций.
(4) 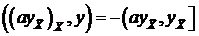 .
.
В соответствии с (4), скалярное произведение (2) запишется в виде:
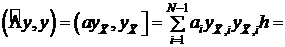 (*)
(*)
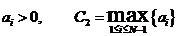 . В соотношении (1), если иметь в виду аппроксимацию ОДУ II-го порядка
. В соотношении (1), если иметь в виду аппроксимацию ОДУ II-го порядка 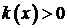 .
.
Следовательно, 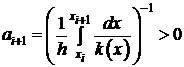 , тогда:
, тогда:
(*) 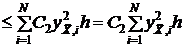
Воспользуемся еще раз формулой (4) в которой 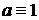 , прочитав ее справа на лево и умножив на (-1).
, прочитав ее справа на лево и умножив на (-1).
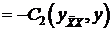 .
.
Вспомним оценку сверху для 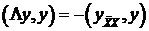 , т.е.
, т.е.
(5) 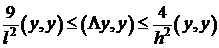 , тогда
, тогда
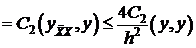 .
.
Итак, получили оценку:
(6) 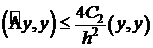 .
.
Будем считать, что 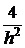 - точная константа в (5).
- точная константа в (5).
___________________________________________________________
?? Можно ли улучшить оценку (6), уменьшив 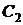 .
.
‼ Получить самостоятельно оценку снизу (7).
___________________________________________________________
(7) 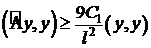 , где
, где 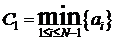 .
.
Приведем без вывода соответствующие оценки – укажем постоянные энергетической эквивалентности для оператора  (двумерный случай):
(двумерный случай):
(8) 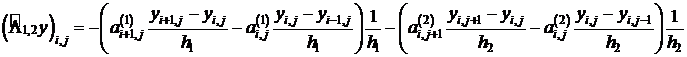 (8) - дискретный аналог (9):
(8) - дискретный аналог (9):
(9) 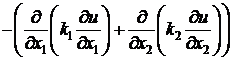 ;
; 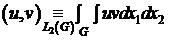 .
.
(10) 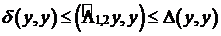 , где
, где
(11) 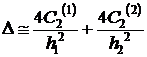 ,
,
(12) 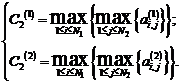
(13) 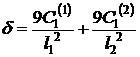 , где
, где
(14) 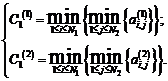
___________________________________________________________
‼ Получить самостоятельно оценки для: а)  и
и  ; б) уточнить формулы (12) и (13).
; б) уточнить формулы (12) и (13).
___________________________________________________________
Корректность операторно-разностных уравнений
Общие сведения
Построенные разностные аналоги краевой задачи для ОДУ II-го порядка, а также задачу Дирихле для уравнения Пуассона, могут быть представлены в виде операторного уравнения:
(1)  .
.
Здесь 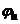 - известная функция правой части из гильбертова пространства сеточных функций,
- известная функция правой части из гильбертова пространства сеточных функций, 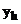 - искомая сеточная функция, которая может считаться финитной при соответствующем переопределении граничных условий и правой части.
- искомая сеточная функция, которая может считаться финитной при соответствующем переопределении граничных условий и правой части.
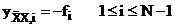 ,
,
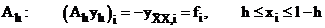 ,
,

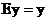 ,
,
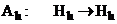 .
.
Пусть нормы 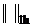 и
и 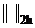 - нормы, введенные на пространстве функций, являющихся решением (1), норма
- нормы, введенные на пространстве функций, являющихся решением (1), норма 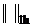 для
для 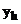 , а норма
, а норма 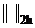 введена на пространстве функций, являющихся правыми частями в (1), т.е. для
введена на пространстве функций, являющихся правыми частями в (1), т.е. для 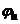 .
.
В простейшем случае эти нормы могут совпадать.
Можно считать, что решение – это множество финитных функций.
Опр. 1
Операторное уравнение (1) называется корректным, если:
1. решение задачи (1) существует и единственно для всех 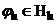 - семейство функций;
- семейство функций;
2. для любой пары 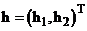 существует
существует  , не зависящая от
, не зависящая от 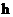 , такая, что выполняется неравенство:
, такая, что выполняется неравенство:
(2)  .
.
Гильбертово пространство финитных функций обозначим 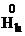 .
.
С пунктом 2) определения корректности, мы встречались ранее, называя его условием устойчивости по правой части. Новым здесь является то, что в левых и правых частях 2) могут фигурировать разные нормы, а также граничные условия, если они есть, учтены в правой части. Неравенство (2) означает, что малым изменениям входных данных соответствует малое изменение возмущений. Т.е. малое по норме изменение функции 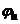 приводит к малому изменению нормы
приводит к малому изменению нормы 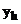 .
.
В формулировке, как и ранее, подразумевается линейность и ограниченность оператора 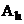 .
.
Докажем последнее утверждение, т.е., на ряду с задачей (1) рассмотрим задачу (3):
(3) 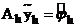 .
.
Вычтем из (3) (1), получим
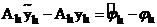 , операторы задач (1), (3), (4) совпадают.
, операторы задач (1), (3), (4) совпадают.
(4) 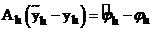 .
.
 .
.
Поскольку 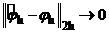 , то, следовательно,
, то, следовательно, 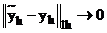 .
.



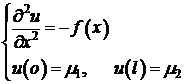
 ;
; .
.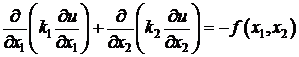 ;
;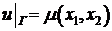 ,
,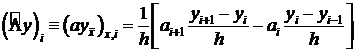 .
.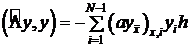 .
.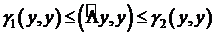 , где константы
, где константы  и не могут быть улучшены.
и не могут быть улучшены.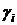 в неравенстве (3) называются постоянными энергетической эквивалентности или энергетическими постоянными.
в неравенстве (3) называются постоянными энергетической эквивалентности или энергетическими постоянными.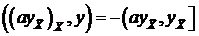 .
.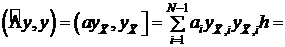 (*)
(*)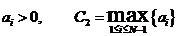 . В соотношении (1), если иметь в виду аппроксимацию ОДУ II-го порядка
. В соотношении (1), если иметь в виду аппроксимацию ОДУ II-го порядка 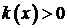 .
.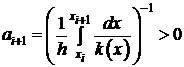 , тогда:
, тогда: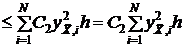
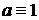 , прочитав ее справа на лево и умножив на (-1).
, прочитав ее справа на лево и умножив на (-1).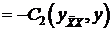 .
.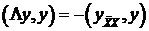 , т.е.
, т.е.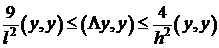 , тогда
, тогда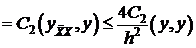 .
.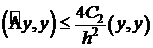 .
.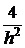 - точная константа в (5).
- точная константа в (5).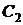 .
.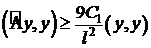 , где
, где 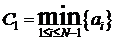 .
. (двумерный случай):
(двумерный случай):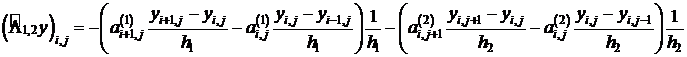 (8) - дискретный аналог (9):
(8) - дискретный аналог (9):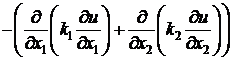 ;
; 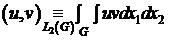 .
.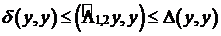 , где
, где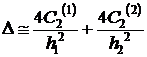 ,
,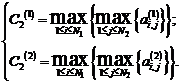
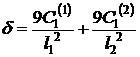 , где
, где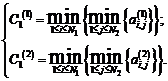
 и
и  ; б) уточнить формулы (12) и (13).
; б) уточнить формулы (12) и (13). .
.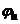 - известная функция правой части из гильбертова пространства сеточных функций,
- известная функция правой части из гильбертова пространства сеточных функций, 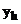 - искомая сеточная функция, которая может считаться финитной при соответствующем переопределении граничных условий и правой части.
- искомая сеточная функция, которая может считаться финитной при соответствующем переопределении граничных условий и правой части.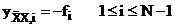 ,
,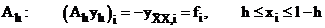 ,
,
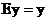 ,
,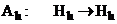 .
.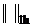 и
и 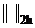 - нормы, введенные на пространстве функций, являющихся решением (1), норма
- нормы, введенные на пространстве функций, являющихся решением (1), норма 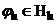 - семейство функций;
- семейство функций;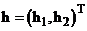 существует
существует  , не зависящая от
, не зависящая от 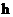 , такая, что выполняется неравенство:
, такая, что выполняется неравенство: .
.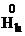 .
.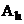 .
.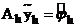 .
.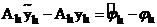 , операторы задач (1), (3), (4) совпадают.
, операторы задач (1), (3), (4) совпадают.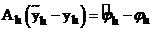 .
. .
.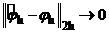 , то, следовательно,
, то, следовательно, 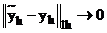 .
.

