Рассмотрим разностную задачу, содержащую оператор левой разностной производной.
(1) 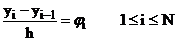 ,
,
(2) 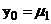 .
.
Корректность задачи Коши для разностного уравнения I-го порядка.
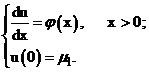
Выразим из (1) 
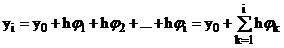 ,
,
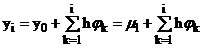 , следовательно,
, следовательно,
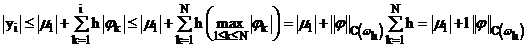 .
.
Так как  , то можно взять максимум от всех
, то можно взять максимум от всех 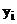 .
.
 , получаем:
, получаем:
 .
.
Таким образом, задача (1), (2) устойчива по начальным данным и правой части.
Свойства оператора левой разностной производной.
(1) 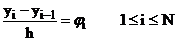 ,
,
(2) 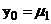 .
.
I. Задачу (1), (2) можно переформулировать таким образом, что:
(3) 
(4) 

Задачу (3), (4) перепишем в виде:
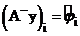 ;
;
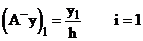 ;
;
 .
.
Для практических нужд полезно построить оператор сопряженный к  .
.
Явное выражение этого оператора чрезвычайно важно.
Опр. 1
Оператор 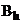 :
: 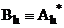 , называется сопряженным к оператору
, называется сопряженным к оператору 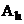 , если выполняется следующее условие
, если выполняется следующее условие
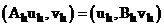
Для этого рассмотрим скалярное произведение вида:
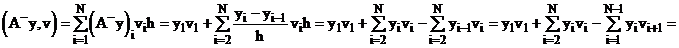
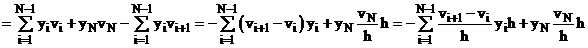 .
.
Таким образом, пришли к следующему равенству:
(5)  .
.
Заметим, что 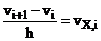 - оператор правой разностной производной.
- оператор правой разностной производной.
Введем оператор правой разностной производной:
(6) 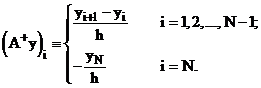
Равенство (5) с учетом соотношения (6) означает, что для оператора левой разностной производной сопряженным является минус оператор правой разностной производной.
Итак,
(7)  (8)
(8) 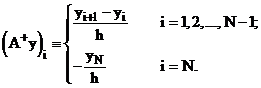
(9) 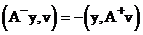 .
.
Известно, что любой линейный оператор 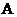 в гильбертовом пространстве сеточных функций можно представить в виде суммы его кососимметрической
в гильбертовом пространстве сеточных функций можно представить в виде суммы его кососимметрической 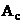 и самосопряженной
и самосопряженной  частей, т.е.
частей, т.е.
(10) 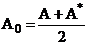 , (11)
, (11) 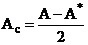 .
.
__________________________________________________________
‼ Показать, что если (11), то  .
.
__________________________________________________________
Построим 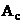 , привлекая в качестве оператора
, привлекая в качестве оператора 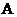 , оператор
, оператор  , задаваемый по формуле (7).
, задаваемый по формуле (7).
 , следовательно,
, следовательно,
(12) 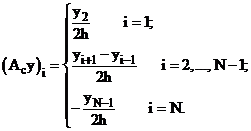
 .
.
Таким образом, мы получили признак кососимметричности оператора:
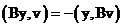 .
.
Поэтому оператор, задаваемый равенством (12), является кососимметрическим. Это означает:
(13) 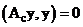 , а следовательно,
, а следовательно,
(14) 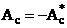 .
.
Вернемся к соотношению (12). Из него следует, что оператор разностной производной второго порядка является кососимметрическим, если в граничных узлах он определен таким образом.
Возможна и другая интерпретация соотношения (12). Оператор А можно считать определенным на расширенной сетке 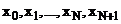 , для которой
, для которой  ,
, 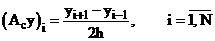 .
.
II. Покажем, что оператор  является положительно определенным, точнее положительным, т.е.
является положительно определенным, точнее положительным, т.е.  .
.
Для этого для любой сеточной функции 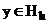 необходимо доказать неравенство:
необходимо доказать неравенство: 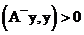 .
.
Воспользуемся формулой (7).

 что и требовалось доказать.
что и требовалось доказать.
Кроме того, было получено соотношение:
(15) 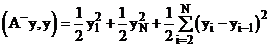 .
.
Каноническая форма двухслойных схем и
Ее применение к исследованию устойчивости
Необходимость введения двухслойных схем вызвана дискретизацией и исследованием эволюционных задач, которые можно записать в виде:
(1) 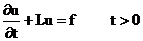 ;
;
(2) 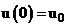 , где
, где 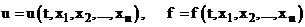 .
.
 - дифференциальный оператор.
- дифференциальный оператор.
(3) 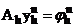 .
.
Для дискретизации задачи (1), (2) неудобно использовать выражение вида (3), т.к. переменная 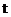 является выделенной в выражении (1), и аппроксимация будет, как минимум, двухточечного шаблона.
является выделенной в выражении (1), и аппроксимация будет, как минимум, двухточечного шаблона.
Так мы приходим к понятию двухслойной разностной схемы.
Каноническая форма.
Пусть Н конечномерное вещественное гильбертово пространство и 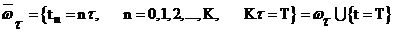 .
.
Обозначим через 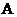 и
и 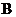 линейные операторы, переводящие
линейные операторы, переводящие 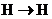 .
.
Операторы 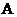 и
и 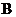 , например, это операторы разностных производных по пространственным переменным. В общем случае они могут зависеть от
, например, это операторы разностных производных по пространственным переменным. В общем случае они могут зависеть от  .
.
Пусть 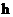 - векторный параметр, от которого зависят операторы
- векторный параметр, от которого зависят операторы 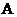 и
и 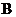 . Считаем, что
. Считаем, что 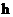 фиксирован.
фиксирован.
Рассмотрим абстрактную задачу Коши операторно-разностного типа.
(4) 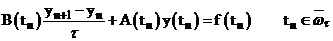 ;
;
(5) 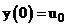 .
.
Можно считать, что задача (4), (5) будет дискретным аналогом задачи (1), (2), если выбрать операторы 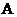 и
и 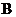 подходящим образом:
подходящим образом: 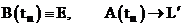 .
.
В уравнении (4) предполагается известными параметр 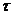 , функция
, функция 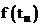 , заданными
, заданными 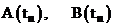 и функция
и функция 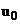 .
.
Считаем, что операторы 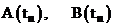 явно не зависят от
явно не зависят от 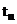 . Также считаем, что оператор
. Также считаем, что оператор 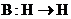 обратим, т.е. существует
обратим, т.е. существует 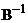 . Условие
. Условие 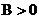 гарантирует обратимость оператора;
гарантирует обратимость оператора; 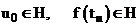 , где
, где 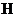 - гильбертово пространство сеточных функций.
- гильбертово пространство сеточных функций.
Рассмотрим теперь задачу (4), (5).
Опр. 1 Двухслойной схемы.
Поставленная выше операторно-разностная задача Коши (4), (5) называется двухслойной схемой, записанной в канонической форме.
Это семейство задач Коши зависящих от параметра 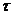 .
.
Введем оператор перехода через все остальные функции, предполагая обратимость оператора В.
 ;
;
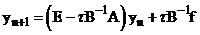 .
.
При достаточно малых значениях параметра 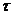 можно определить оператор
можно определить оператор 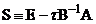 называемый оператором перехода.
называемый оператором перехода.
Введем также обозначения:
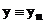 ;
; 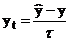 ;
;  ;
;
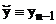 ;
; 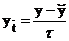 ;
; 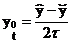 .
.
Тогда схему (4), (5) можно записать в виде:
(6) 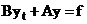 ;
;
(7) 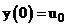 .
.



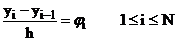 ,
,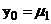 .
.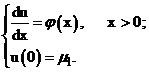

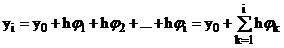 ,
,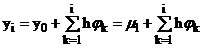 , следовательно,
, следовательно,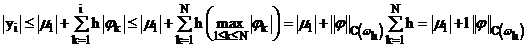 .
. , то можно взять максимум от всех
, то можно взять максимум от всех 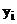 .
. , получаем:
, получаем: .
.


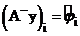 ;
;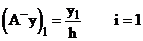 ;
; .
. .
.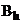 :
: 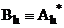 , называется сопряженным к оператору
, называется сопряженным к оператору 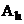 , если выполняется следующее условие
, если выполняется следующее условие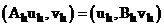
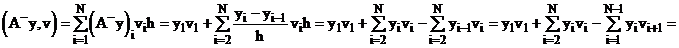
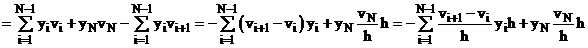 .
. .
.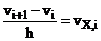 - оператор правой разностной производной.
- оператор правой разностной производной.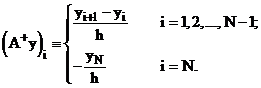
 (8)
(8) 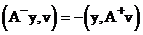 .
.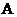 в гильбертовом пространстве сеточных функций можно представить в виде суммы его кососимметрической
в гильбертовом пространстве сеточных функций можно представить в виде суммы его кососимметрической 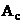 и самосопряженной
и самосопряженной  частей, т.е.
частей, т.е. 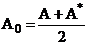 , (11)
, (11) 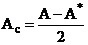 .
. .
. , следовательно,
, следовательно,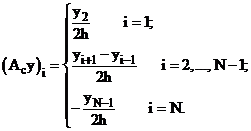
 .
.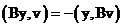 .
.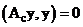 , а следовательно,
, а следовательно,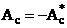 .
.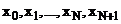 , для которой
, для которой  ,
, 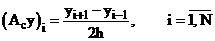 .
. .
.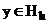 необходимо доказать неравенство:
необходимо доказать неравенство: 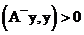 .
.
 что и требовалось доказать.
что и требовалось доказать.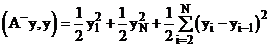 .
.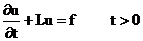 ;
;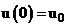 , где
, где 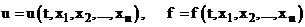 .
. - дифференциальный оператор.
- дифференциальный оператор.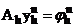 .
.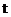 является выделенной в выражении (1), и аппроксимация будет, как минимум, двухточечного шаблона.
является выделенной в выражении (1), и аппроксимация будет, как минимум, двухточечного шаблона.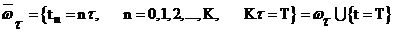 .
.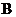 линейные операторы, переводящие
линейные операторы, переводящие 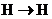 .
. .
.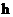 - векторный параметр, от которого зависят операторы
- векторный параметр, от которого зависят операторы 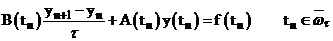 ;
;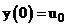 .
.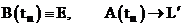 .
.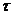 , функция
, функция 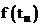 , заданными
, заданными 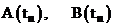 и функция
и функция 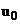 .
.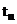 . Также считаем, что оператор
. Также считаем, что оператор 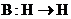 обратим, т.е. существует
обратим, т.е. существует 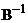 . Условие
. Условие 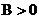 гарантирует обратимость оператора;
гарантирует обратимость оператора; 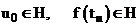 , где
, где 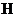 - гильбертово пространство сеточных функций.
- гильбертово пространство сеточных функций. ;
;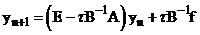 .
.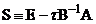 называемый оператором перехода.
называемый оператором перехода.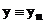 ;
; 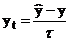 ;
;  ;
; 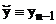 ;
; 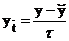 ;
; 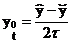 .
.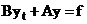 ;
;


