Для двухслойной схемы (6), (7) будем рассматривать множество решений, зависящих от 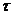 как от параметра, а также от входных данных: начального условия
как от параметра, а также от входных данных: начального условия 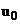 и правой части
и правой части  .
.
Опр. 2
Говорят, что схема(6), (7) корректна (корректно поставлена), если для достаточно малых значений 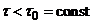 :
:
1. решение задачи (6), (7) существует и единственно;
2. для любых  существуют
существуют 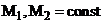 , независящие от
, независящие от 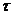 и
и 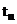 , параметра
, параметра 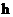 , такие, что выполняется неравенство:
, такие, что выполняется неравенство:
(8)  .
.
Условие 2) является определением устойчивости (6), (7) по начальным данным и правой части.
Можно отдельно ввести условие устойчивости по начальным данным.
В приложениях возникает потребность получать более сильные по сравнению с (8) оценки устойчивости по начальным данным.
Опр. 3
Схема (6), (7) называется 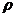 -устойчивой по начальным данным, если для любого n:
-устойчивой по начальным данным, если для любого n: 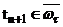 выполняется неравенство:
выполняется неравенство:
(9)  , где
, где 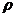 -константа независящая от
-константа независящая от  ;
;  .
.
Нетрудно видеть, что достаточным условием 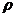 -устойчивости (9), является ограниченность оператора перехода S:
-устойчивости (9), является ограниченность оператора перехода S: 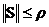 .
.
Действительно, при однородной правой части имеем:  .
.
(10) 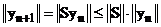 , если
, если 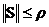 , то приходим к (9).
, то приходим к (9).
Замечание.
1. в определение 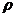 - устойчивости, как правило, используются значения
- устойчивости, как правило, используются значения 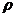 близкие к единице.
близкие к единице.
Например,  ,
,
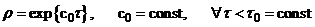 .
.
2. в определение корректности двухслойной схемы в условии устойчивости (8) часто используется несколько другая форма:
вместо  (8) используют
(8) используют
(8′) 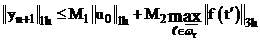 .
.
Очевидно, что  также является нормой, которую можно обозначить
также является нормой, которую можно обозначить  .
.
В соответствии с формой (8) и (8′), а также учтя отдельно начальные данные сформируем две задачи:
I.
(12)  ;
;
(13)  ;
;
II.
(14)  ;
;
(15)  .
.
Для этих задач должно выполняться:
(16)  ;
;
(17)  .
.
 , а, следовательно, и
, а, следовательно, и
 .
.
Оказывается, нет необходимости отдельно исследовать устойчивость по правой части, если схема 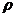 -устойчива по начальным данным. Точнее имеет место теорема.
-устойчива по начальным данным. Точнее имеет место теорема.
Теорема 1
(18)  ;
;
(19)  .
.
Если задача (18), (19) равномерно устойчива по начальным условиям (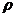 -устойчива относительно начальных данных) в норме
-устойчива относительно начальных данных) в норме  . Тогда она устойчива и по правой части и имеет место оценка:
. Тогда она устойчива и по правой части и имеет место оценка:
 ,
,
где  ,
,  .
.
Доказательство:
Выразим из (18)  , предполагая, как и везде
, предполагая, как и везде  .
.
 .
.
Очевидно неравенство:
(*) 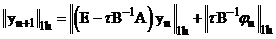 .
.
Решим вспомогательную задачу, оценив сверху норму оператора перехода.
Покажем, что  ,
, 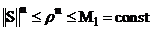 .
.
Заметим, что 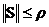 . Действительно, сформулируем вспомогательную задачу, отличающуюся от задачи (18), (19) однородной правой частью.
. Действительно, сформулируем вспомогательную задачу, отличающуюся от задачи (18), (19) однородной правой частью.
 ;
;
 .
.
Из того, что схема (7), (8) 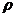 - устойчива следует выполнение:
- устойчива следует выполнение:
(20)  ,
,
(21)  ,
, 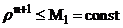 .
.
Возьмем норму от обеих частей равенства (20).
(22)  .
.
Используем наименьшую норму оператора  из его возможных норм.
из его возможных норм.
Сравнивая (22) и (21), можем считать, что 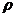 фигурирующее в определении (21) удовлетворяет неравенству.
фигурирующее в определении (21) удовлетворяет неравенству.
Оценка (22) достигается в конечномерном случае при определенном выборе вектора 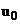 .
.
Строго говоря, надо было указать  .
.
В случае если  и
и 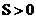 этого можно добиться выбором
этого можно добиться выбором  .
.
 , то в роли функции
, то в роли функции  , можно подставить собственную функцию оператора
, можно подставить собственную функцию оператора  , которая соответствует собственному значению. Мы добьемся выполнения (22).
, которая соответствует собственному значению. Мы добьемся выполнения (22).
Вернемся к соотношению (*), где 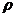 - постоянная, фигурирующая в определении
- постоянная, фигурирующая в определении 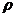 - устойчивости.
- устойчивости.
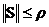 ,
, 


1.7.4. Необходимое и достаточное условие устойчивости в НА
Энергетическое пространство
Пусть  - гильбертово пространство сеточных функций и задан оператор А с областью определения
- гильбертово пространство сеточных функций и задан оператор А с областью определения  и выполняются соотношения:
и выполняются соотношения:
1.  ,
,
2. 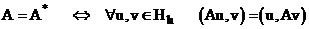 ,
,
3. оператор 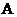 является линейным оператором.
является линейным оператором.
Примерами такого оператора могут быть:
1)  будет финитным в
будет финитным в  , т.е.
, т.е. 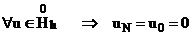 , тогда он положительно определен и является самосопряженным.
, тогда он положительно определен и является самосопряженным.
2)  , предполагаем, что
, предполагаем, что  ,
,
 ,
,  для всех
для всех 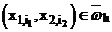
Опр. 1 Энергетического пространства.
Энергетическим пространством  называется линейное нормированное пространство сеточных функций в котором скалярное произведение любых двух сеточных функций
называется линейное нормированное пространство сеточных функций в котором скалярное произведение любых двух сеточных функций  определяется следующим образом
определяется следующим образом
(1)  . Норма в
. Норма в  определяется по формуле
определяется по формуле
(2) 
__________________________________________________________
‼ Проверить аксиомы скалярного произведения.
__________________________________________________________
Теорема А.А. Самарского.
Пусть дана двухслойная разностная схема вида:
(3) 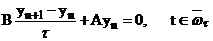 ;
;
(4)  ;
;
(5)  .
.
Тогда для равномерной устойчивости схемы (3), (4) по начальным данным с  необходимо и достаточно выполнение операторного неравенства:
необходимо и достаточно выполнение операторного неравенства:
(6)  , т.е. должно выполняться
, т.е. должно выполняться 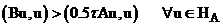 .
.
Доказательство:
В соответствии с теоремой требуется доказать, что для выполнения неравенств
(7) 
необходимо и достаточно выполнение неравенства (6) при условии (5) для схемы (3), (4).
Достаточность.
Перепишем (3) в компактной форме.

Умножим обе части полученного равенства на  .
.
(8)  .
.
Заметим, что
(9)  ;
;
подставим (9) в (8).


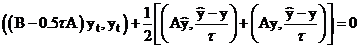
(10) 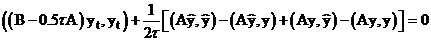
Равенство (10) носит название основного энергетического тождества.
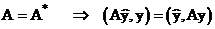
С учетом введенной ранее энергетической нормой (2) последнее равенство (10) перепишется:
(11) 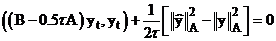 - вторая форма основного энергетического тождества.
- вторая форма основного энергетического тождества.
Опустим первое слагаемое, принимая во внимание (6), а точнее  , получим:
, получим:
(13) 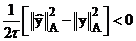 , следовательно,
, следовательно,  .
.
Поскольку n – любое, то достаточность доказана.
(14)  .
.
Замечание.
Если неравенство (6) нестрогое, то неравенства (12), (13), (14) также будут нестрогими.
Свойство 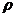 - устойчивости с
- устойчивости с  при этом также выполняется.
при этом также выполняется.
Необходимость.
Указание: воспользоваться энергетическим тождеством в форме (11).
Положим в (11) 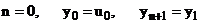 , учтем, что справедливо соотношение
, учтем, что справедливо соотношение 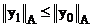 , так как
, так как 
 , где
, где 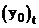 может быть любой функцией из
может быть любой функцией из  .
.
При n=0 схема имеет вид:
 .
.
Выберем  произвольно.
произвольно.
Покажем, что всегда найдется элемент  , который удовлетворяет задаче (3), (4). Фактически мы его найдем.
, который удовлетворяет задаче (3), (4). Фактически мы его найдем.
 , так как оператор обратим, то есть,
, так как оператор обратим, то есть,  , то
, то
(15)  , умножим на
, умножим на  , найдем требуемую функцию
, найдем требуемую функцию  .
.
 .
.
Таким образом, мы приходим к неравенству для произвольной функции 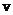 .
.
 , что и означает
, что и означает  .
.
Замечание.
Пусть 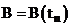 , т.е. зависит от временного слоя. Тогда выполнение неравенства
, т.е. зависит от временного слоя. Тогда выполнение неравенства  для любых
для любых 
 гарантирует
гарантирует 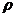 -устойчивость с
-устойчивость с  схемы (3), (4).
схемы (3), (4).
Пример 1.
Исследовать устойчивость неявной схемы для уравнения теплопроводности.
(16) 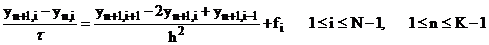 ;
;
(17) 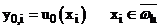 ;
;
(18) 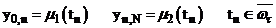 .
.
Граничные условия (18) можно учесть в функции правой части  , таким образом, что их можно считать нулевыми, т.е.
, таким образом, что их можно считать нулевыми, т.е. 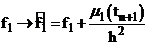 ,
, 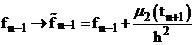 .
.
По теореме 1, из 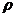 - устойчивости по начальным данным следует
- устойчивости по начальным данным следует  - устойчивости по правой части.
- устойчивости по правой части.
Изучение задачи (16)-(18) сводится к изучению 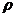 - устойчивости, если таковая имеется, по начальным данным.
- устойчивости, если таковая имеется, по начальным данным.
Запишем соответствующую двухслойную схему.
(19) 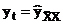 ;
;
(20)  .
.
Получим каноническую форму двухслойной схемы.
(21) 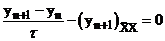 .
.
Ранее было показано, что  - оператор положительно определен
- оператор положительно определен
(22)  - самосопряжен.
- самосопряжен.
Используя (22) можно переписать (21) в виде:
(23)  .
.
В канонической форме (23) будет иметь вид: 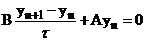 . Получим ее.
. Получим ее.
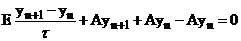 ,
,
 ,
,
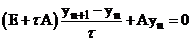 .
.
Сравнивая с формой (3), видим, что 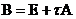 .
.
Проверим операторное неравенство  .
.

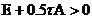 . Поскольку
. Поскольку  , то последнее неравенство выполняется.
, то последнее неравенство выполняется.
Пример 2.
Исследовать устойчивость. Получить достаточные условия устойчивости для уравнения теплопроводности.
Явная схема для уравнения теплопроводности имеет вид:
(24) 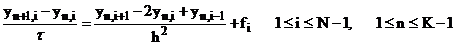 ;
;
(17) 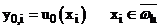 ;
;
(18) 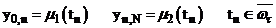 .
.
Проведя аналогичные рассуждения, что и в первой задаче, мы приходим к виду:
(25) 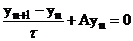 , где
, где  ,
,
(26)  .
.
Сравнивая с канонической формой (3), видим, что 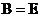 .
.
Определим значение шага по времени  , гарантирующего выполнение операторного неравенства
, гарантирующего выполнение операторного неравенства 
То есть надо найти такие 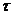 для которых выполняется операторное неравенство.
для которых выполняется операторное неравенство.
Легко показать, что
(27)  .
.
__________________________________________________________
‼ Доказать самостоятельно (27).
__________________________________________________________
Итак, имеем цепочку 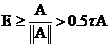 , т.е. выполнение неравенства
, т.е. выполнение неравенства 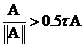 - достаточное условие выполнения неравенства
- достаточное условие выполнения неравенства  .
.
 , в силу линейности оператора
, в силу линейности оператора  , поскольку,
, поскольку, 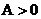 , то
, то  , а, следовательно,
, а, следовательно,
(28)  .
.
Ранее было выведено достаточное условие для  , тогда получим
, тогда получим  , что совпадает с результатом, который можно получить методом гармоник.
, что совпадает с результатом, который можно получить методом гармоник.
Выражение (28) показывает, что явная схема приводит к достаточно жестким ограничениям на шаг по времени.
Пусть  , тогда
, тогда 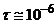 и число шагов по времени будет составлять порядка
и число шагов по времени будет составлять порядка  . Желательно не превышать число шагов по времени
. Желательно не превышать число шагов по времени  , так как число
, так как число  может обесценить результат при накоплении ошибок.
может обесценить результат при накоплении ошибок.
Это и есть основной недостаток явных схем, зато преимуществом является ее простота – приводит к диагональным матрицам.
Формально явные схемы допускают любой шаг по времени, однако он не может быть слишком велик.
Далее будет рассмотрено понятие асимптотической устойчивости применительно к уравнению теплопроводности.
При 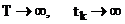 , решение уравнения теплопроводности выходит на так называемый регулярный режим, и его вид определяется собственной функцией и соответствующим ей минимальным собственным значением оператора задачи.
, решение уравнения теплопроводности выходит на так называемый регулярный режим, и его вид определяется собственной функцией и соответствующим ей минимальным собственным значением оператора задачи.
Правильная передача такого поведения дискретной задачи обеспечивается свойством устойчивости асимптотической модели, которая в свою очередь приводит к  .
.





 как от параметра, а также от входных данных: начального условия
как от параметра, а также от входных данных: начального условия 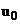 и правой части
и правой части  .
.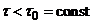 :
: существуют
существуют 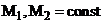 , независящие от
, независящие от 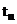 , параметра
, параметра 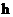 , такие, что выполняется неравенство:
, такие, что выполняется неравенство: .
.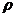 -устойчивой по начальным данным, если для любого n:
-устойчивой по начальным данным, если для любого n: 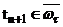 выполняется неравенство:
выполняется неравенство: , где
, где  ;
;  .
.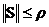 .
. .
.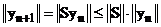 , если
, если  ,
,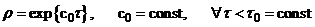 .
.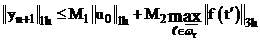 .
. также является нормой, которую можно обозначить
также является нормой, которую можно обозначить  .
. ;
; ;
; ;
; .
. ;
; .
. , а, следовательно, и
, а, следовательно, и  .
. ;
; .
. . Тогда она устойчива и по правой части и имеет место оценка:
. Тогда она устойчива и по правой части и имеет место оценка: ,
, ,
,  .
. , предполагая, как и везде
, предполагая, как и везде  .
. .
.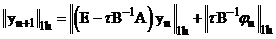 .
. ,
, 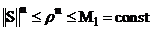 .
. ;
; .
. ,
, ,
, 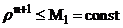 .
. .
. из его возможных норм.
из его возможных норм. .
. и
и 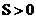 этого можно добиться выбором
этого можно добиться выбором  .
. , то в роли функции
, то в роли функции 


 - гильбертово пространство сеточных функций и задан оператор А с областью определения
- гильбертово пространство сеточных функций и задан оператор А с областью определения  и выполняются соотношения:
и выполняются соотношения: ,
,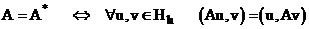 ,
,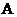 является линейным оператором.
является линейным оператором. будет финитным в
будет финитным в  , т.е.
, т.е. 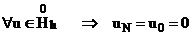 , тогда он положительно определен и является самосопряженным.
, тогда он положительно определен и является самосопряженным. , предполагаем, что
, предполагаем, что  ,
, ,
,  для всех
для всех 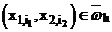
 называется линейное нормированное пространство сеточных функций в котором скалярное произведение любых двух сеточных функций
называется линейное нормированное пространство сеточных функций в котором скалярное произведение любых двух сеточных функций  определяется следующим образом
определяется следующим образом . Норма в
. Норма в 
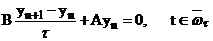 ;
; .
. необходимо и достаточно выполнение операторного неравенства:
необходимо и достаточно выполнение операторного неравенства: , т.е. должно выполняться
, т.е. должно выполняться 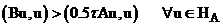 .
.

 .
. .
. ;
;

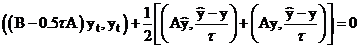
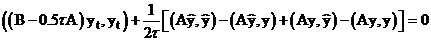
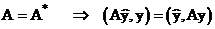
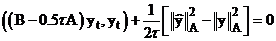 - вторая форма основного энергетического тождества.
- вторая форма основного энергетического тождества. , получим:
, получим: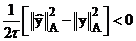 , следовательно,
, следовательно,  .
. .
.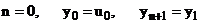 , учтем, что справедливо соотношение
, учтем, что справедливо соотношение 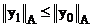 , так как
, так как 
 , где
, где 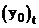 может быть любой функцией из
может быть любой функцией из  .
. произвольно.
произвольно. , который удовлетворяет задаче (3), (4). Фактически мы его найдем.
, который удовлетворяет задаче (3), (4). Фактически мы его найдем. , так как оператор обратим, то есть,
, так как оператор обратим, то есть,  , то
, то , умножим на
, умножим на  , найдем требуемую функцию
, найдем требуемую функцию  .
.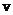 .
. , что и означает
, что и означает  .
.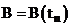 , т.е. зависит от временного слоя. Тогда выполнение неравенства
, т.е. зависит от временного слоя. Тогда выполнение неравенства  для любых
для любых 
 гарантирует
гарантирует 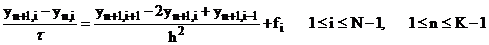 ;
;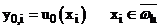 ;
;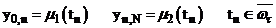 .
. , таким образом, что их можно считать нулевыми, т.е.
, таким образом, что их можно считать нулевыми, т.е. 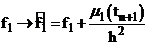 ,
, 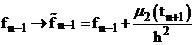 .
.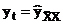 ;
;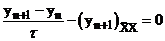 .
. - оператор положительно определен
- оператор положительно определен - самосопряжен.
- самосопряжен. .
.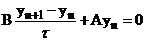 . Получим ее.
. Получим ее.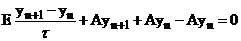 ,
, ,
,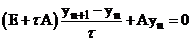 .
.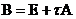 .
.
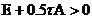 . Поскольку
. Поскольку  , то последнее неравенство выполняется.
, то последнее неравенство выполняется.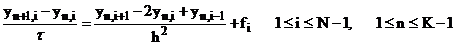 ;
;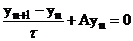 , где
, где  ,
,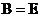 .
. , гарантирующего выполнение операторного неравенства
, гарантирующего выполнение операторного неравенства  .
.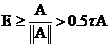 , т.е. выполнение неравенства
, т.е. выполнение неравенства 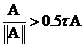 - достаточное условие выполнения неравенства
- достаточное условие выполнения неравенства  , в силу линейности оператора
, в силу линейности оператора  , поскольку,
, поскольку, 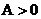 , то
, то  , а, следовательно,
, а, следовательно, .
. , тогда получим
, тогда получим  , что совпадает с результатом, который можно получить методом гармоник.
, что совпадает с результатом, который можно получить методом гармоник. , тогда
, тогда 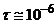 и число шагов по времени будет составлять порядка
и число шагов по времени будет составлять порядка  . Желательно не превышать число шагов по времени
. Желательно не превышать число шагов по времени  , так как число
, так как число  может обесценить результат при накоплении ошибок.
может обесценить результат при накоплении ошибок.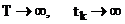 , решение уравнения теплопроводности выходит на так называемый регулярный режим, и его вид определяется собственной функцией и соответствующим ей минимальным собственным значением оператора задачи.
, решение уравнения теплопроводности выходит на так называемый регулярный режим, и его вид определяется собственной функцией и соответствующим ей минимальным собственным значением оператора задачи. .
.


