Различные физические процессы (распространение тепла или колебаний в среде, процессы газодинамики и аэродинамики) характеризуются некоторыми интегральными законами сохранения (тепла, массы, количества движения, энергии). При выводе дифференциальных уравнений математической физики обычно исходят из некоторого интегрального соотношения (уравнения баланса), выражающего закон сохранения для малого объема. Дифференциальное уравнение получается из уравнения баланса при стягивании объема к нулю в предположении существования непрерывных производных, входящих в уравнение.
Одно из основных свойств разностной схемы является ее консервативность. Разностная схема называется консервативной, если для нее выполняются разностные аналоги физических законов сохранения. Для получения консервативных разностных схеме естественно исходить из уравнений баланса, записанных для элементарных объемов (ячеек) сеточной области. Входящие в эти уравнения баланса интегралы и производные следует заменить приближенными разностными выражениями. В результате получаем однородную разностную схему. Такой метод получения консервативных схем будем называть интегро-интерполяционным методом (методом баланса).
Итак, метод позволяет строить разностные схемы, удовлетворяющие основным законам сохранения, если этим законам удовлетворяют соответственные непрерывные модели.
Метод рассмотрим на примере краевой задачи для ОДУ второго порядка вида:
 (1)
(1)
 (2)
(2)
 (3)
(3)
В уравнении (1) и условии (2) искомой является функция 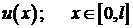 . Функции
. Функции 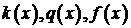 и постоянные
и постоянные 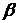 ,
, 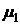 ,
,  задаются. Относительно этих функции будем предполагать, что
задаются. Относительно этих функции будем предполагать, что
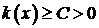 ,
, 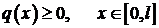 и
и 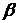 ≥ 0.
≥ 0.
Кроме того, будем предполагать, что все функции имеют необходимую по ходу изложения гладкость. При указанных условиях решение задачи (1), (2), (3) существует и единственно.
Уравнение (1) можно рассматривать как уравнение установившегося распределения температуры u(x) в стержне длины l, на одном конце которого поддерживается заданная температура, а на другом происходит теплообмен с окружающей средой.
Для построения решения разностной схемы будем использовать равномерную сетку: 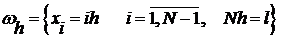 ;
;
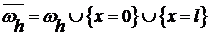 ;
;
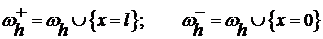 ;
;
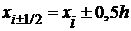 .
.
Проинтегрируем обе части уравнения (1) по отрезку
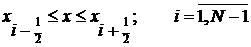 .
.
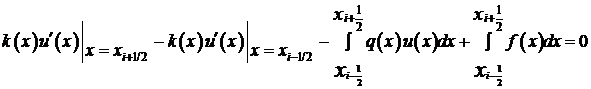 . (4)
. (4)
Будем предполагать, что 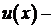 температура. Поток тепла внутри тела
температура. Поток тепла внутри тела
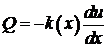 .
.
Уравнение (2) является несколько измененной формой теплообмена по закону Ньютона.
Введем функцию теплового потока:
 . (5)
. (5)
Тогда уравнение (4) может быть переписано в виде:
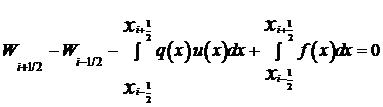 . (4׳)
. (4׳)
Используем приближенные замены (6-8):
 . (6)
. (6)
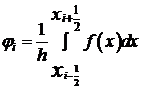 . (7)
. (7)
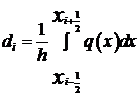 , (8)
, (8)
получим из (4׳) приближенное равенство, которое заменим на точное, не меняя для простоты прежние обозначения.
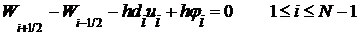 . (9)
. (9)
Выразим значение функции 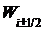 , используя значения функции
, используя значения функции 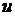 (х) в узлах сетки. Из уравнения (5) получаем, что
(х) в узлах сетки. Из уравнения (5) получаем, что
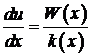 .
.
Интегрируя соотношение на отрезке 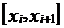 , имеем:
, имеем:
.
 .
.
Здесь
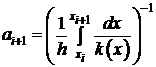 . (10)
. (10)
Переходя к точным равенствам, получаем:
 , (11)
, (11)
аналогично
 . (12)
. (12)
Подставим (11) и (12) в равенство (9) получаем:
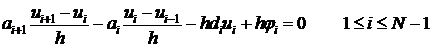 .
.
Разделим обе части полученного равенства на 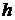 :
:
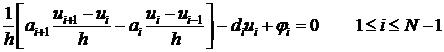 . (13)
. (13)
Разностная аппроксимация уравнения (1) построена.
По сравнению с непосредственной аппроксимацией возникли особенности в вычислении коэффициентов разностных уравнений:
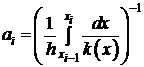 .
.
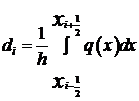 .
.
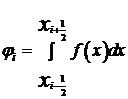 .
.
Аппроксимация граничного условия (3) очевидна:
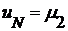 . (14)
. (14)
С граничным условием (2) необходимо аппроксимировать. Для получения его дискретного аналога воспользуемся интегро – итерполяционным методом.
Проинтегрируем обе части уравнения (1) по отрезку  , тогда
, тогда
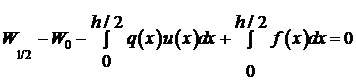 .
.
Из условия (2): 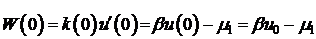 .
.
Из условия (12): 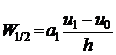 . Подставляя значения в предыдущее уравнение, получаем
. Подставляя значения в предыдущее уравнение, получаем
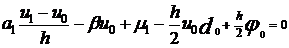 ; (15)
; (15)
Где 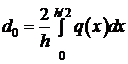 ;
; 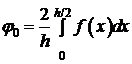 .
.
Формула (15) аппроксимирует граничное условие (2). Таким образом, разностная схема (13), (14), (15) построена.
Полученное разностное граничное условие (15) можно записать:
 . (16).
. (16).
Т.о. краевое условие (2) имеет разностным аналогом уравнение(16).
В дальнейшем решение разностной задачи в отличии от решения дифференциальной задачи будем обозначать буквой y, так что yi = y (xi), 
Объединяя уравнений (13), (16) получаем дискретную модель для задачи (1) – (3):
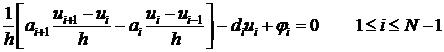
(17)
 ; yN = µ2.
; yN = µ2.
При исследовании дискретной модели (17) возникают следующие вопросы:
1) о существовании и единственности решения системы линейных алгебраических уравнений (17); 2) каким методом надо решать эту систему; 3) вопрос об аппроксимации дифференциальной задачи (1) – (3) разностной схемой (17); 4) сходиться решение разностной задачи к решению дифференциальной задачи при 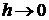 ? На первые два вопроса можно ответить, преобразуя систему (17) к системе с ленточной треугольной матрицей:
? На первые два вопроса можно ответить, преобразуя систему (17) к системе с ленточной треугольной матрицей:

Где 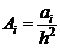 ,
, 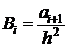 ,
,  и
и  .
.
Граничные условия можно записать в виде:
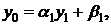
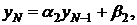 здесь
здесь
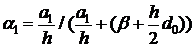 ;
;  и
и
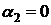 ,
, 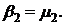
Из условия ai >0, β≥0, d i ≥0 следует, что 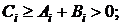 т. е. выполнены условия устойчивости прогонки. Систему (17) можно решать методом скалярной прогонки. На последние два вопроса ответы даются в следующих параграфах.
т. е. выполнены условия устойчивости прогонки. Систему (17) можно решать методом скалярной прогонки. На последние два вопроса ответы даются в следующих параграфах.



 (1)
(1) (2)
(2) (3)
(3)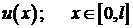 . Функции
. Функции 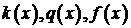 и постоянные
и постоянные 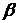 ,
, 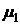 ,
,  задаются. Относительно этих функции будем предполагать, что
задаются. Относительно этих функции будем предполагать, что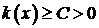 ,
, 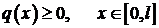 и
и 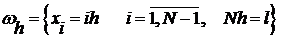 ;
;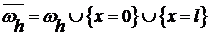 ;
;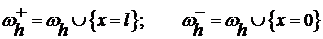 ;
;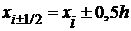 .
.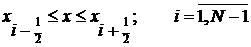 .
. 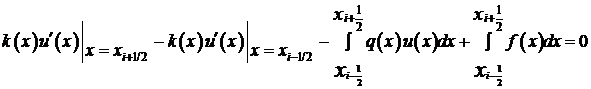 . (4)
. (4)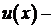 температура. Поток тепла внутри тела
температура. Поток тепла внутри тела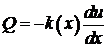 .
. . (5)
. (5)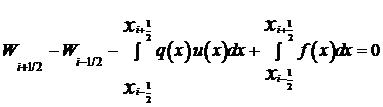 . (4׳)
. (4׳) . (6)
. (6)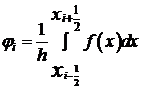 . (7)
. (7)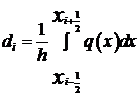 , (8)
, (8)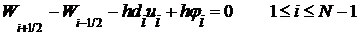 . (9)
. (9)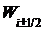 , используя значения функции
, используя значения функции 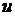 (х) в узлах сетки. Из уравнения (5) получаем, что
(х) в узлах сетки. Из уравнения (5) получаем, что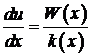 .
.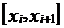 , имеем:
, имеем: .
.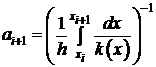 . (10)
. (10) , (11)
, (11) . (12)
. (12)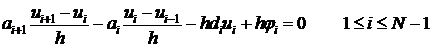 .
.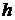 :
: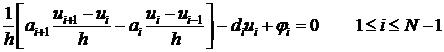 . (13)
. (13)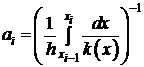 .
.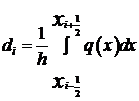 .
.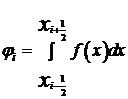 .
.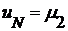 . (14)
. (14) , тогда
, тогда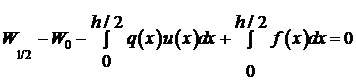 .
.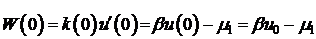 .
.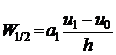 . Подставляя значения в предыдущее уравнение, получаем
. Подставляя значения в предыдущее уравнение, получаем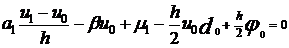 ; (15)
; (15)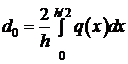 ;
; 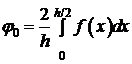 .
. . (16).
. (16).
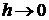 ? На первые два вопроса можно ответить, преобразуя систему (17) к системе с ленточной треугольной матрицей:
? На первые два вопроса можно ответить, преобразуя систему (17) к системе с ленточной треугольной матрицей:
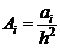 ,
, 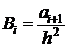 ,
,  и
и  .
.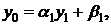
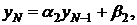 здесь
здесь 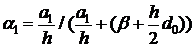 ;
;  и
и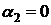 ,
, 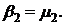
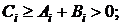 т. е. выполнены условия устойчивости прогонки. Систему (17) можно решать методом скалярной прогонки. На последние два вопроса ответы даются в следующих параграфах.
т. е. выполнены условия устойчивости прогонки. Систему (17) можно решать методом скалярной прогонки. На последние два вопроса ответы даются в следующих параграфах. 

