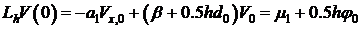 .
.
 .
.
Если выбрать произвольную гладкую функцию  , то нетрудно показать, что
, то нетрудно показать, что 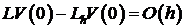
и эта оценка не улучшаема.
Однако если рассматривать функцию 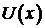 - решение задачи (1), (2):
- решение задачи (1), (2):
 . (1)
. (1)
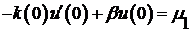 , (2)
, (2)
то оценка может быть улучшена.
Рассмотрим и покажем что:
 . (*)
. (*)
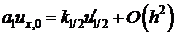 . (3)
. (3)
Так как
 . (4)
. (4)
и
 ,
,
то
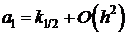 . (5)
. (5)
Подставим (4) и (5) в (3) получим:
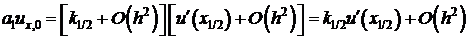 .
.
Вспоминая, что

получаем
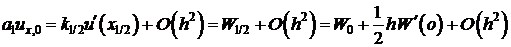 . (6)
. (6)
Здесь  .
.
Преобразуем разностное граничное условие х=0 с учетом (6).
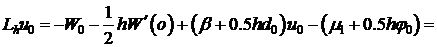
 .
.
Поскольку граничное условие
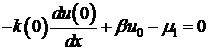 ,
,
то мы получаем:
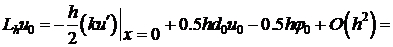
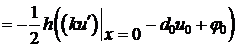 . (7)
. (7)
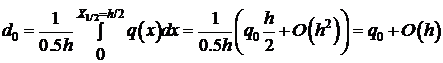 . (8)
. (8)
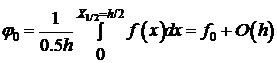 . (9)
. (9)
Подставим (8), (9) в (7).
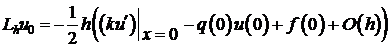 . (10)
. (10)
Выражение 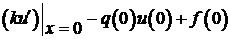 представляет собой левую часть дифференциального уравнения (1) которая выполняется и для х=0
представляет собой левую часть дифференциального уравнения (1) которая выполняется и для х=0
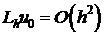 .
.
Условие на правой границе задается точно  и в исследовании не нуждается.
и в исследовании не нуждается.
В итоге получаем оценку (*) к которой мы и стремились.
1.4.5. Понятие о погрешности аппроксимации, устойчивости и сходимости разностной схемы на примере краевой задачи для ОДУ второго порядка
Ранее интегро – интерполяционным методом была построена модель, состоящая из разностных уравнений:
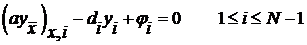 . (1)
. (1)
 . (2)
. (2)
Решение этой задачи есть вектор  .
.
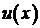 - решение задачи с непрерывным оператором.
- решение задачи с непрерывным оператором.
Пользователю важно знать погрешность, введем ее как
 . (3)
. (3)
Мы имеем семейство задач (1-2) которые зависят от 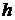 как от параметра, размерность решения устремляется к бесконечности, если устремить шаг к нулю.
как от параметра, размерность решения устремляется к бесконечности, если устремить шаг к нулю.
Подставим выражение (3) в задачу (1) и (2).
 . (4)
. (4)
 . (5)
. (5)
Заметим, что все разностные операторы являются линейными(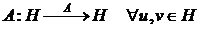 ,
,  числа
числа 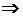
 )
)
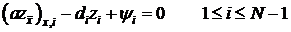 . (6)
. (6)
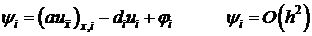 . (7)
. (7)
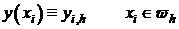 - решение дискретной задачи,
- решение дискретной задачи,
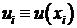 - решение непрерывной задачи.
- решение непрерывной задачи.

Разностное граничное условие (5) запишется в виде:
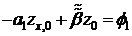 , (8)
, (8)
 , (9)
, (9)
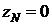 . (10)
. (10)
Задача для погрешности (6), (8), (10) поставлена.
Перед тем, как провести рассуждения относительно погрешности, сформулируем определение сходимости разностного решения.
Определение Локальной сходимости.
Решение разностной задачи 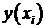 сходится к решению непрерывной задачи
сходится к решению непрерывной задачи  с порядком m>0 в точке
с порядком m>0 в точке 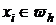 , если
, если 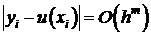 , h – шаг сетки.
, h – шаг сетки.
На практике используют понятие глобальной сходимости или сходимости по норме. Это в свое время требует введения какой-либо нормы в пространстве функций, определенных на сетке.
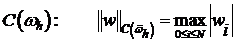
или 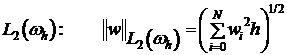
введем определение глобальной сходимости решения разностной задачи.
Определение Глобальной сходимости.
Решение разностной задачи 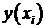 сходится к решению непрерывной задачи
сходится к решению непрерывной задачи  с порядком m>0, если
с порядком m>0, если
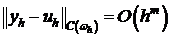 ,
,
где 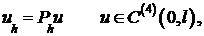
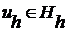 - определена на сетке,
- определена на сетке, 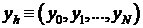 .
.
Структура задачи (6), (8), (10) совпадает со структурой задачи (1), (2), поэтому целесообразны следующие утверждения.
Определение. Разностная схема (1), (2) устойчива по правой части и граничному условию, если для произвольных правых частей 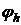 , для любых шагов сетки справедливо неравенство:
, для любых шагов сетки справедливо неравенство:
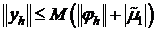 , где М= const>0 не зависящая от h. (12)
, где М= const>0 не зависящая от h. (12)
Оценки вида (12) называют априорными. Получением такого вида оценок занимается теория устойчивости.
Предположим, что оценка вида (12) для задачи (1), (2) выполняется. Тогда сразу следует сходимость разностной задачи (1), (2) к решению непрерывной задачи (1), (2) из параграфа 1, если функция решения спроектирована в  .
.
В соответствии с оценкой (12) для задачи (6)-(10) справедливо неравенство:
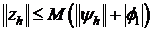 .
.
Ранее было показано, что 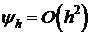
 , поэтому
, поэтому
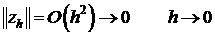 .
.
Более общее утверждение называемое теоремой Лакса – Филиппова.
Теорема Лакса – Филиппова. Для линейных разностных задач из аппроксимации и устойчивости следует сходимость, причем скорость сходимости m совпадает с порядком аппроксимации  .
.



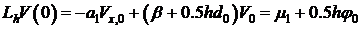 .
. .
. , то нетрудно показать, что
, то нетрудно показать, что 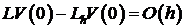
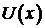 - решение задачи (1), (2):
- решение задачи (1), (2): . (1)
. (1)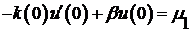 , (2)
, (2) . (*)
. (*)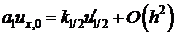 . (3)
. (3) . (4)
. (4) ,
,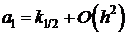 . (5)
. (5)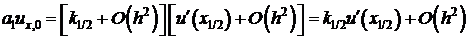 .
.
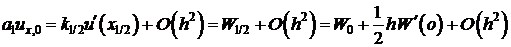 . (6)
. (6) .
.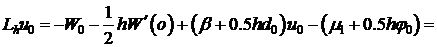
 .
.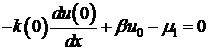 ,
,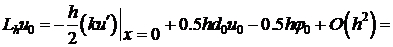
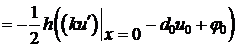 . (7)
. (7)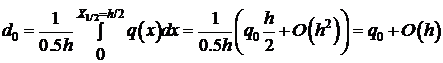 . (8)
. (8)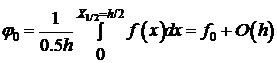 . (9)
. (9)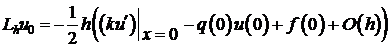 . (10)
. (10)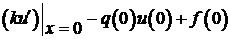 представляет собой левую часть дифференциального уравнения (1) которая выполняется и для х=0
представляет собой левую часть дифференциального уравнения (1) которая выполняется и для х=0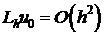 .
. и в исследовании не нуждается.
и в исследовании не нуждается.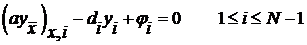 . (1)
. (1) . (2)
. (2) .
.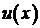 - решение задачи с непрерывным оператором.
- решение задачи с непрерывным оператором. . (3)
. (3)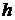 как от параметра, размерность решения устремляется к бесконечности, если устремить шаг к нулю.
как от параметра, размерность решения устремляется к бесконечности, если устремить шаг к нулю. . (4)
. (4) . (5)
. (5)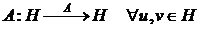 ,
,  числа
числа 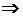
 )
)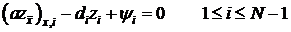 . (6)
. (6)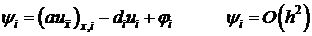 . (7)
. (7)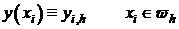 - решение дискретной задачи,
- решение дискретной задачи,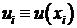 - решение непрерывной задачи.
- решение непрерывной задачи.
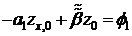 , (8)
, (8) , (9)
, (9)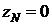 . (10)
. (10)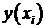 сходится к решению непрерывной задачи
сходится к решению непрерывной задачи  с порядком m>0 в точке
с порядком m>0 в точке 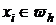 , если
, если 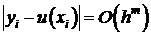 , h – шаг сетки.
, h – шаг сетки.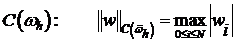
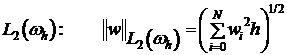
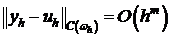 ,
,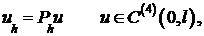
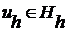 - определена на сетке,
- определена на сетке, 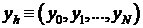 .
.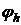 , для любых шагов сетки справедливо неравенство:
, для любых шагов сетки справедливо неравенство: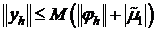 , где М= const>0 не зависящая от h. (12)
, где М= const>0 не зависящая от h. (12) .
.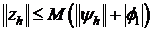 .
.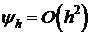
 , поэтому
, поэтому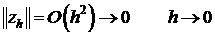 .
. .
.


