Взаимные эквивалентные преобразования схем с соединением сопротивлений в виде треугольника (рис. 2.10, а) и звезды (рис. 2.10,6) иногда могут привести к облегчению решения задачи по расчету цепи.
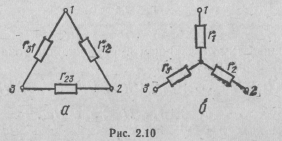
Для эквивалентности преобразований таких схем необходимо, чтобы сопротивления между любой парой точек 1, 2, 3 в треугольнике и звезде были одинаковыми при любых сопротивлениях в непреобразованной части цепи, в том числе и при сопротивлениях, равных бесконечности.
В последне м случае будем иметь:
Считая известными сопротивления сторон треугольника  и
и  , найдем неизвестные сопротивления лучей эквивалент н ой звезды
, найдем неизвестные сопротивления лучей эквивалент н ой звезды 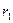 ,
, 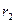 и
и 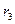 . Для этого из
. Для этого из
равенства (2. 13) почленно вычтем раве н ство (2. 15) и прибавим равенство (2. 14). При этом получим
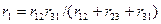 . (2.16)
. (2.16)
Ан алогичным образом н айдем
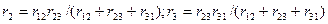 (2. 1 7)
(2. 1 7)
Из получе н ных выражений видно, что сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивле н ий трех сторон треугольника.
Для обратного преобразования звезды в эквивале н т н ый треугольник необходимо сопротивления сторон треугольника  ,
,  и
и 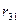 выразить через сопротивле н ия лучей звезды
выразить через сопротивле н ия лучей звезды 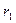 , r 2 и
, r 2 и 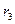 . Для этого из выражений для
. Для этого из выражений для 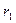 , r 2 и
, r 2 и 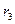 получим
получим
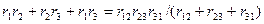 . (2. 1 8)
. (2. 1 8)
Р а зделив это равенство на каждое из равенств, определяющих 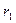 , r 2 и
, r 2 и 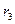 , найдем
, найдем
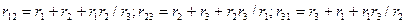 (2.19)
(2.19)
Из этих выражений видно, что сопротивление сторо н ы треугольника равно сумме сопротивлений прилегающих лучей звезды и их произведения, деленного на сопротивление третьего луча.
Пример 2.2.
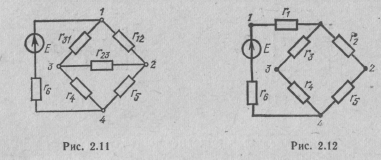
В электрической цепи, схема которой приведена на рис. 2.11, известны э. д. с. E=30 В и все сопротивления: 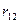 =8 Ом;
=8 Ом; 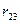 =12 Ом;
=12 Ом; 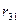 = 12 Ом;
= 12 Ом; 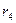 =5,5 Ом;
=5,5 Ом; 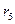 =7 О м;
=7 О м; 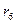 =2 О м. Определить ток в ветви с источником э. д. с. Е.
=2 О м. Определить ток в ветви с источником э. д. с. Е.
Решение.
Заменив треугольник сопротивлений 123 звездой сопротивлений (рис. 2.12), в соответствии с выражениями (2.16) и (2.17) найдем сопротивления звезды:
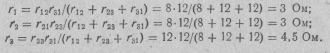
Сопротивление между точками 1 и 4:

Ток в ветви с источником э. д. с. Е:
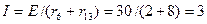 A.
A.
Рассмотренный пример показывает, что с помощью эквивалент н ых преобразований схем с соединением сопротивлений в виде треугольника и звезды иногда
от сложной электрической цепи (см. рис. 2.11) удается перейти к простой (см. рис. 2.12), где сопротивления соединены последовательно и параллельно. Это можег значительно упростить решение задачи на расчет цени.
2.3.3. Преобразование схем с источниками э. д. с. и тока
При расчетах электрических цепей иногда оказывается целесообразным от схемы замещения реального источника электрической энергии, заданной в виде источника э.д.с. (рис. 2.13), пе-

рейти к схеме замещения в виде источника тока (рис. 2.14) или осуществить обратный переход.
Для эквивалентной замены источников необходимо, чтобы токи и напряжения на выходе источников при заданной нагрузке остались без изменений.
Условия эквивалентности источников э.д.с. и тока найдем из выражений для токов и напряжений на выходе источников.
Для источника э.д.с. (см. рис. 2.13)
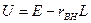 (2.20)
(2.20)
или
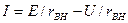 (2.21)
(2.21)
Для источника тока (см. рис. 2.14)
I = J - g вн Г (2-22)
или
 (2.23)
(2.23)
Из выражений (2.21) и (2.22) видно, что при замене источника э.д.с. источником тока его ток I и проводимость gBH будут равны:
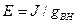 и g вн=1/ r вн. (2.24)
и g вн=1/ r вн. (2.24)
Из выражений (2.20) и (2.23) следует, что при замене источника тока источником э.д.с. параметры источника э.д.с. Е и гвя будут равны:
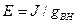
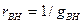 . (2.25)
. (2.25)
Переход от одного источника к другому может привести к облегчению решения задачи по расчету электрических цепей. Рассмотрим это на примере,
Пример 2.3.
В схеме электрической цепи, изображенной на рис. 2.15, известно: E1 = 6 В; E2 = 3 В; r 1 = r 2 = r 3 = 10 Ом. Найти ток в ветви с сопротивлением r3
Решение.
Перейдя от источников э. д. с. к источникам тока, получим эквивалентную схему, изображенную на рис. 2.16, где
J1 =E1/ r1 = 6/10 = 0,6 A; g1 = 1/г1 =1/10 = 0,1 См;
J2 = E2/r2 = 3/10 = 0,3 A; g2 = 1/Г2 = 1/10 = 0,1 См.
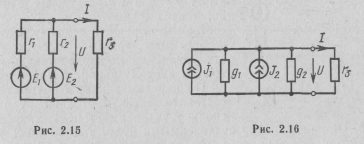
Источники тока образуют один эквивалентный источник тока (рис. 2.17), где
Jэ = J1 + J2 = 0,6 + 0,3 = 0,9 A; gэ = gl +g2 =0,1 +0,1 =0,2 См.
Перейдя от источника тока (см. рис. 2.17) к источнику э. д. с., получим схему цепи (рис. 2.18), эквивалентную исходной схеме, где
Еэ = Jэ /gэ = 0,9/0,2 = 4,5 В; rэ = l/gэ = 1/0,2 = 5 Ом.
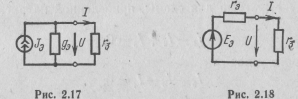
Искомый ток в ветви с сопротивлением ra в этой схеме
I 3 = Eэ/(rэ + r 3) = 4,5/(5 + 10) = 0,3 А.
Рассмотренный пример показывает, что эквивалентные преобразования источников так же, как и преобразования сопротивлений, соединенных в виде звезды и треугольника, иногда позволяют перейти от сложной электрической цепи к простой, что облегчает ее расчет.
Рассмотренные в настоящем подразделе эквивалентные преобразования схем представляют собой основной метод расчета несложных цепей с одним источником энергии. Этот метод можно назвать методом эквивалентных преобразований. При расчете сложных цепей с помощью методов, рассматриваемых в последующих подразделах, часто оказывается целесообразным предварительное преобразование части схемы цепи.
МЕТОД УРАВНЕНИЙ КИРХГОФА
Самым общим методом расчета сложных электрических цепей является метод уравнений Кирхгофа. Сущность этого метода состоит в составлении системы уравнений в соответствии с первым и вторым законами Кирхгофа и решении этой системы относительно неизвестных токов.
 Если сложная электрическая цепь имеет y узлов и в ветвей, а следовательно, в неизвестных токов, то необходимо составить и решить систему в линейно независимых уравнений. Покажем, что эти уравнения можно составить по первому и второму законам Кирхгофа.
Если сложная электрическая цепь имеет y узлов и в ветвей, а следовательно, в неизвестных токов, то необходимо составить и решить систему в линейно независимых уравнений. Покажем, что эти уравнения можно составить по первому и второму законам Кирхгофа.
По первому закону Кирхгофа можно составить всего столько уравнений, сколько узлов имеет цепь, т. е. у уравнений. Однако линейно независимыми будут только y —1 уравнений. Это следует из того, что после сложения у —1 уравнений, составленных для всех узлов, кроме одного, получим уравнение, в которое входят только токи, сходящиеся в последнем узле, так как остальные токи войдут в сумму два раза с противоположными знаками и сократятся. Это уравнение будет отличаться от уравнения для последнего узла только знаками токов. Умножим его на —1, получим уравнение для последнего узла.
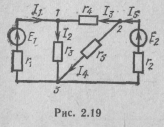
Для иллюстрации этого положения составим уравнения по первому закону Кирхгофа для схемы, приведенной на рис. 2.19: для первого узла
I1-I2 + I3 = 0; (2.26)
для второго узла
I5-I3-I4 = 0; (2.27)
для третьего узла
I2-I1+I4-I5 = 0. (2.28)
Сложив выражения (2.26) и (2.27), получим
-I2 + I1-I4+I5 = 0.
Умножим это уравнение на —1, получим уравнение для третьего узла (2.28), т. е. уравнение для последнего узла можно получить линейными комбинациями из уравнений, составленных по первому закону Кирхгофа для первых y —1 узлов. Таким образом, для цепи, имеющей y узлов, по- первому закону Кирхгофа можно составить у — 1 линейно независимых уравнений.
Остальные n =в — (у —1) линейно независимые уравнения составляются по второму закону Кирхгофа.
Для того чтобы показать это, воспользуемся топологическими свойствами электрической цепи. Так как при добавлении связи графа к дереву графа схемы электрической цепи образуется один
контур, то число связей графа схемы равно числу независимых контуров электрической цепи. Если учесть, что дерево графа содержит все узлы электрической цепи, число которых равно y, а число ветвей на дереве графа на единицу меньше числа узлов, т. е. равно y — 1, то общее число ветвей в цепи будет
в=(у-1)+ n, (2.29)
где п — число связей графа схемы электрической цепи, равное числу независимых контуров.
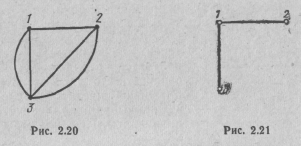
Отсюда получается выражение для определения числа связей дерева графа, а следовательно, и числа независимых контуров электрической цепи
n = в-(у-1) (2.30)
Для иллюстрации этого рассмотрим схему электрической цепи, приведенную на рис. 2.19. Граф схемы этой цепи приведен на рис. 2.20, а одно из деревьев графа схемы — на рис. 2.21. Дерево графа этой цепи содержит три узла и две ветви, т. е. y — 1 ветвей. Число связей графа схемы равно трем. Так как всего ветвей на графе пять, то, следовательно, выполняется соотношение для числа связей графа схемы (2.30), а значит, и для числа независимых контуров
n =в-(у-1)=5-(3-1)=3
Таким образом, для цепи, имеющей y узлов и в ветвей, по второму закону Кирхгофа можно составить n =в— (у— 1) линейно независимых уравнений. При этом общее число уравнений, составленных по первому и второму законам Кирхгофа, будет равно числу ветвей, т. е. числу неизвестных токов, что позволяет найти токи во всех ветвях электрической цепи.
Расчет цепей с помощью законов Кирхгофа целесообразно производить в следующем порядке:
1. Определить число узлов y и число ветвей вв цепи. В соответствии с этим определить количество уравнений, которые необходимо составить по первому и второму законам Кирхгофа.
2. Обозначить на схеме цепи токи в ветвях и произвольно выбрать их положительные направления. Выбрать независимые кон-
туры цепи. Это целесообразно сделать таким образом, чтобы в каждый последующий контур входила хотя бы одна новая ветвь. Произвольно задаться направлением обхода контуров.
3. Составить y —1 уравнений по первому закону Кирхгофа.
4. Составить n =в - (у - 1) уравнений по второму закону Кирхгофа. При составлении этих уравнений э. д. с. считаются положительными, если их направление совпадает с направлением обхода контуров. Падение напряжения будет положительным, если направление обхода контура совпадает с выбранным направлением тока.
 5. Решить составленную систему уравнений относительно неизвестных токов. Если при этом некоторые токи получатся отрицательными, то это означает, что их действительные направления противоположны первоначально выбранным положительным направлениям. Поясним это на примере.
5. Решить составленную систему уравнений относительно неизвестных токов. Если при этом некоторые токи получатся отрицательными, то это означает, что их действительные направления противоположны первоначально выбранным положительным направлениям. Поясним это на примере.
Пример 2.4.
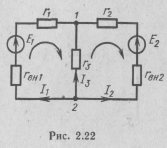
В цепи, изображенной на рис. 2.22, даны ее элементы: E 1 = 50 B; E 2 =1O В; rвн 1 = 0,4 Ом; rвн2=l,0 Ом; r1= 3 Ом; r2=2 Ом; r3=2 Ом. Требуется определить токи в ветвях.
Решение.
В схеме два узла и три ветви. Следовательно, по первому закону Кирхгофа необходимо составить одно уравнение, а но второму — два уравнения.
Обозначим на схеме цепи токи в ветвях и стрелками укажем их положительные направления. Выберем два независимых контура и стрелками покажем направления их обхода.
Составим уравнение по первому закону Кирхгофа для первого узла:
I1 + I2 + 1з = 0.
Составим уравнения по второму закону Кирхгофа для выбранных независимых контуров:
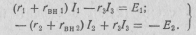
Подставляя в последние два уравнения численные значения пар а метров элементов цепи и переписав первое уравнение, получим систему из трех уравнений:
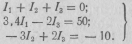
Решим эту систему, найдем: I 1 =10 A; I 2 = -2 A; I 3 = -8 A. Действительное направление тока I 1 совпадает, а токов I 2 и I 3 противоположно их выбранным положительным направлениям.
Проверку правильности расчета токов можно осуществить по балансу мощностей или по выполнению законов Кирхгофа для любого из узлов и контуров цепи.
При расчете электрических цепей с помощью законов Кирхгофа источники электрической энергии можно задавать не только ввиде источников э. д. с., но и в виде источников тока, которые учитываются при составлении уравнений по первому закону Кирхгофа.
Достоинством рассмотренного метода расчета сложных электрических цепей с помощью законов Кирхгофа является его общность, а недостатком — громоздкость (большое число уравнений, равное числу ветвей). Поэтому разработан ряд методов и приемов, упрощающих расчет. Впоследующих подразделах рассмотрим некоторые из этих методов, применимых только для линейных электрических цепей.
МЕТОД КОНТУРНЫХ ТОКОВ
 Расчет сложных электрических цепей методом контурных токов сводится крешению системы уравнений, составленных только по второму закону Кирхгофа. Этих уравнений получается только n = в — (y — 1), т. е. на (y —1) меньше, чем при расчете цепи методом уравнений Кирхгофа. Это облегчает расчет сложных цепей.
Расчет сложных электрических цепей методом контурных токов сводится крешению системы уравнений, составленных только по второму закону Кирхгофа. Этих уравнений получается только n = в — (y — 1), т. е. на (y —1) меньше, чем при расчете цепи методом уравнений Кирхгофа. Это облегчает расчет сложных цепей.
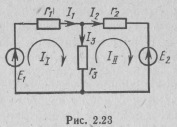
Сущность этого метода рассмотрим на примере расчета цепи, схема которой приведена на рис. 2.23. Система уравнений, составленных для этой цепи по первому и второму законам Кирхгофа, имеет вид:
 (2.31)
(2.31)
Исключим из этой системы уравнений ток I 3, протекающий вветви, входящей одновременно в два контура. Этот ток равен
I3=I1-I2.
Подставив его в уравнения, составленные по второму закону Кирхгофа, получим:
 или
или

Эта система уравнений дает основание считать, что в каждом независимом контуре протекает свой, так называемый контурный ток, который независимо от других токов создает падение напряжения на тех сопротивлениях цепи, по которым он протекает. Контурные токи обычно обозначаются буквой I с римскими индексами. В рассматриваемой схеме, приведенной на рис. 2.23, направление контурных токов II и I II показано стрелками внутри контуров. Эти токи равны токам в ветвях I 1 и I 2, по которым протекает только один из контурных токов, т. е. II = I 1 и III = I 2
При расчете электрических цепей рассматриваемым методом кроме контурных токов вводят еще ряд понятий: контурные э. д. с., собственные и взаимные сопротивления.
Контурной э. д. с. называют алгебраическую сумму всех э. д. с. контура. При этом обход контура производят по направлению контурного тока и э. д. с. берут со знаком «плюс», если ее направление совпадает с направлением контурного тока, и со знаком «минус», если эти направления противоположны. Контурные э. д. с. обычно обозначают буквой Е с римскими индексами, которые соответствуют номерам контуров.
В рассматриваемом примере контурные э. д. с. EI = Е1 и Е II =- E 2
Собственным сопротивлением контура называют сумму всех сопротивлений, входящих в данный контур. При этом каждое сопротивление берется с положительным знаком. Собственные сопротивления контуров обозначаются буквой rс двойными индексами, соответствующими номеру контура.
В рассматриваемом примере собственные сопротивления контуров r 11 = r 1 + r 3 и r 22= r 2 + r 3.
Взаимными сопротивлениями контуров называют сопротивления, одновременно входящие в два разных контура. Они обозначаются буквой r с двумя индексами, первый из которых соответствует номеру рассматриваемого контура, а второй — номеру контура, имеющего общее сопротивление с рассматриваемым контуром. Взаимные сопротивления считаются положительными, если контурные токи, протекающие по этим сопротивлениям, имеют одинаковое направление, и отрицательными, если направления контурных токов противоположны.
В рассматриваемом примере взаимное сопротивление первого контура со вторым r 12 =- r 3, а второго контура с первым r 21 =- r 3. Отсюда видно, что r 21 =- r 21, т. е. взаимные сопротивления, отличающиеся одно от другого порядком индексов, равны между собой. Это справедливо только для электрических цепей, не содержащих зависимых источников э. д. с. или тока.
C учетом введенных понятий систему уравнений (2.33) для рассматриваемого примера можно записать в виде:
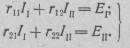 (2.34)
(2.34)
Решив эту систему уравнений, найдем контурные токи II и III. Если некоторые из этих токов получаются отрицательными, то их действительные направления будут противоположны первоначально принятым положительным направлениям. Зная контурные токи, можно найти токи в ветвях. Если в ветви протекает только один контурный ток, то истинный ток в ветви будет равен этому току. Токи в ветвях, по которым протекают несколько контурных токов, равны их алгебраической сумме.
В общем случае для электрической цепи, содержащей п неза-. висимых контуров, система контурных уравнений имеет вид:
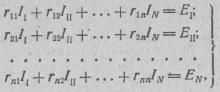 (2.35)
(2.35)
где 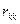 -собственное сопротивление k-го контура;
-собственное сопротивление k-го контура;
rhj — взаимное сопротивление k-го и j-го контуров;
Ek — контурная э.д.с. k-го контура.
Решая эту систему уравнений с помощью определителей, найдем ток в любом k-м контуре
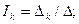 (2.36)
(2.36)
где Δ — определитель системы:
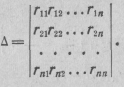
Этот определитель для пассивных цепей, не содержащих зависимых источников э. д. с. и тока, симметричен относительно его главной диагонали, так как для таких цепей любые взаимные сопротивления rkj и rjk равны между собой.
Определитель 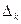 получается из определителя Δ путем замены k-го столбца свободными членами:
получается из определителя Δ путем замены k-го столбца свободными членами:
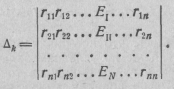
Разлагая в выражении (2.36) определитель Δk по элементам k-го столбца, получим
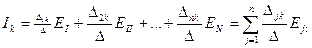 (2.37)
(2.37)
где Δjk — алгебраическое дополнение определителя системы, которое получается путем вычеркивания в нем j-й строки и k-го столбца и умножения на (—l)j+k
При расчете электрических цепей методом контурных токов целесообразно придерживаться следующего порядка:
1. Выбрать независимые контуры цепи и указать положительные направления контурных токов в них.
2. Вычислить собственные и взаимные сопротивления контуров, а также контурные э. д. с.
3. Составить систему уравнений для контурных токов в соответствии со вторым законом Кирхгофа.
4. Решить полученную систему уравнений одним из известных методов, т. е. определить контурные токи.
5. Определить токи в ветвях. Рассмотрим это на примере.
Пример 2.5.
В электрической цепи, схема которой приведенана рис. 2.23, дан о: E1 = 6 В; E2 = 3 В; r 1 = r 2 = r 3 = 1 Ом. Требуется определить токи в ветвях.
Решение.
В схеме два независимых контура. Покажем положительные направления контурных токов II и III ·. стрелками на схеме цепи. Собственные сопротивле н ия контуров 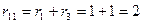 Ом;
Ом; 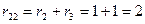 Ом.
Ом.
Взаимные сопротивления 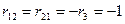 Ом.
Ом.
Контурные э. д. с. E I = E 1= 6 В; Е II = e 1 = -3 В.
Подставив эти значения в стандартную форму системы контурных уравнений (2.34), получим:

Из первого уравнения 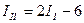 .
.
Подставим это во второе уравнение, п о лучим:
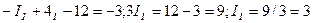 А;
А;
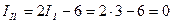
Токи в ветвях:
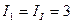 А;
А; 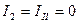 ;
; 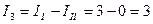 А
А
Выше предполагалось, что источники энергии заданы в виде источников э.д. с. Если же по условиям задачи часть источников энергии будет задана в виде источников тока, то эти источники можно заменить согласно правилу, изложенному в подразд. 2.3, эквивалентными источниками э. д. с. или же рассчитать электрическую цепь с заданными источниками тока. В последнем случае NT независимых контуров целесообразно выбирать таким образом, чтобы каждый из них включал один источник тока. Контурные токи в этих контурах будут равны токам источников. Остальные k =в—(y — 1 )— NT независимых контура следует выбирать таким образом, чтобы в них не входили ветви с заданными источниками тока. Для определения контурных токов в последних контурах для них составляются по второму закону Кирхгофа k уравнений.
Система контурных уравнений (2.35) может быть записана в матричной форме:
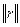
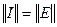 (2.38)
(2.38)
Где 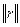 — квадратная матрица сопротивлений цепи порядка п;
— квадратная матрица сопротивлений цепи порядка п;
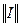 — матрица-столбец искомых контурных токов;
— матрица-столбец искомых контурных токов;
|| Е ||— матрица-столбец контурных э. д. с., причем:
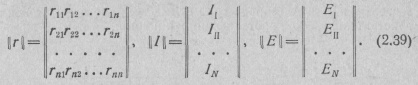
Для того чтобы решить матричное уравнение (2.38), умножим обе его части слева на обратную матрицу ||r||-1:

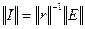
Так как  =
= 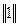 , то
, то
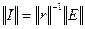 (2.40)
(2.40)
При решении несложных задач по расчету электрических цепей применять матричный метод не всегда целесообразно. Однако этот метод вобщем случае имеет ряд преимуществ. Матричная форма записи более экономна в отношении занимаемого ею места и действий над нею. Такой вид записи открывает более широкие возможности для решения уравнений с помощью вычислительных машин.
Взаключение следует отметить, что контурные токи вобщем случае являются расчетными величинами, а реально существующими токами являются токи, протекающие в ветвях электрической цепи.
Достоинством рассмотренного метода контурных токов является меньшее число уравнений по сравнению с методом уравнений Кирхгофа и возможность формализации решения, что позволяет рассчитывать очень сложные электрические цепи с применением вычислительных машин.
МЕТОД НАЛОЖЕНИЯ
Метод наложения, применяемый для расчета электрических цепей, основан на принципе наложения, который утверждает, что ток в любой ветви линейной электрической цепи, содержащей несколько источников э. д. с., можно рассматривать как алгебраическую сумму частичных токов, созданных в этой ветви действием каждой э. д. с. в отдельности.
Справедливость этого принципа следует непосредственно из выражения (2.37)
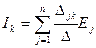 ,
,
полученного в предыдущем подразделе. Действительно, если в этом выражении положить все э.д. с., кроме Е 1, равными нулю, то по-
лучим частичный ток в k-й ветви I ' k , вызванный действием только э. д. с. Е 1. Если считать Е2 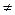 0, аостальные э. д. с. равными нулю, то получим частичный ток I " k, вызванный действием только э. д. с. Е2, и т. д. Алгебраическая сумма всех частичных токов даст действительный ток, протекающий в k-й ветви.
0, аостальные э. д. с. равными нулю, то получим частичный ток I " k, вызванный действием только э. д. с. Е2, и т. д. Алгебраическая сумма всех частичных токов даст действительный ток, протекающий в k-й ветви.
Этот принцип применим не только к токам, но и к напряжениям, так как они линейно связаны с токами. К расчету же мощности этот принцип применить нельзя, так как мощность является не линейной, а квадратичной функцией тока или напряжения. Па самом деле, если по участку цепи с сопротивлением r проходит ток I = I 1+ I 2, то мощность Р = rI 2 = r (I 1 + I 2)2 = 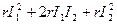 , а не
, а не 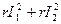 , как следовало бы из принципа наложения.
, как следовало бы из принципа наложения.
Применение принципа наложения к расчету электрических цепей составляет содержание метода наложения. Используя этот метод, можно найти токи в ветвях без составления и решения системы уравнений, а непосредственно по закону Ома. При этом вначале находят частичные токи от действия каждого источника э. д. с. в отдельности, принимая остальные э. д. с. равными нулю и оставляя в схеме только их внутренние сопротивления, а затем— действительные токи как алгебраические суммы частичных токов.
Рассмотрим это на примере.
Пример 2.6.
Найти ток в ветви с источником э. д. с. Е2 в схеме цепи, изображенной на рис. 2.22, если E1 = 50 В; E2=10 В; r BH1 = O,4 Ом; r BH2=l Ом; r 1= 3 Ом; r 2=2 Ом; r s=2 Ом.
Р ешение.
Приняв Е2=0, получим схему, приведенную на рис.2.24. Для определения
частичного тока I2, созданного вветви с источником э. д. с. E2, найдем вначале напряжение между точками 1 и 2.
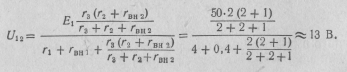
Частичный ток
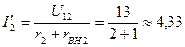 А.
А.
Этот ток направлен от узла 1 к узлу 2.
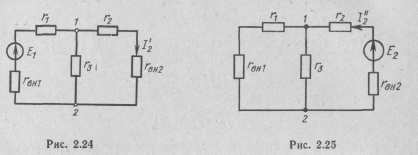
Приняв E 1= 0,получим схему, приведенную на рис.2.25. Частичный ток врассматриваемой ветви найдем по закону Ома:
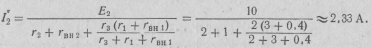
Этот ток направлен от узла 2 кузлу 1. Действительный ток в ветви 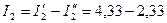 = 2 A направлен от узла 1 к узлу 2.
= 2 A направлен от узла 1 к узлу 2.
В заключение следует отметить, что метод наложения применим только к линейным электрическим цепям.
МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ
 Расчет сложных электрических цепей методом узловых потенциалов, или узловых напряжений, сводится к решению системы уравнений, составленных только по первому закону Кирхгофа. Из этих уравнений определяют напряжения в узлах схемы электрической цепи относительно некоторого базисного узла, потенциал которого принимают равным нулю, а токи в ветвях, соединяющих узлы, находят по закону Ома.
Расчет сложных электрических цепей методом узловых потенциалов, или узловых напряжений, сводится к решению системы уравнений, составленных только по первому закону Кирхгофа. Из этих уравнений определяют напряжения в узлах схемы электрической цепи относительно некоторого базисного узла, потенциал которого принимают равным нулю, а токи в ветвях, соединяющих узлы, находят по закону Ома.
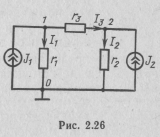
Сущность этого метода рассмотрим на примере электрической цепи (рис. 2.26), источники энергии которой заданы в виде источников тока.
Потенциал одного из узлов, например нулевого, зафиксируем и будем считать его равным нулю. Такой узел обычно называют базисным узлом. При этом потенциалы остальных узлов будут равны напряжениям между этими узлами и базисным узлом.
Выбрав положительные направления токов составим уравнения по первому закону Кирхгофа для незаземленных узлов:
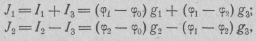
где g 1 = l/ r 1; g 2 =1/r2; g3 = l/r3.
Учитывая, что φθ=0, после преобразования получим:

Обозначив g 11 = g 1 + g 3; g 22 = g 2 + g 3 ; g 12 = g 21 =- g 3
получим:
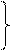 g11φ1 + g12φ2 = J1;
g11φ1 + g12φ2 = J1;
g21φ1 + g22φ2 = J2. (2·41)
В общем случае для электрической цепи, имеющей гс+1 узлов, система уравнений для определения узловых потенциалов будет иметь вид:
 g11φ1 + g12φ2 +... + g1nφn = J1;
g11φ1 + g12φ2 +... + g1nφn = J1;
g21φ1 + g22φ2 +... + g2nφn = J2;
.......................... (2.42)
gn1φ1 + gn2φ2 +... + gnnφn = Jn,
где gkk — собственная проводимость k-гo узла, равная сумме проводимостей всех ветвей, соединенных с этим узлом; эта проводимость всегда положительна;
gkj — взаимная проводимость между k-м и j-м узлами, равная сумме проводимостей ветвей, соединяющих эти узлы; эта проводимость при выбранном направлении всех узловых напряжений к базисному узлу для цепей, не содержащих зависимых источников электрической энергии, всегда отрицательна;
Jk — узловой ток k-ro узла, равный алгебраической сумме токов источников тока, подсоединенных к fe-му узлу, эти токи берутся со знаком «плюс», если они направлены к узлу, и со знаком «минус», если направлены от узла. Выше предполагалось, что источники электрической энергии заданы в виде источников тока. Если в схеме электрической цепи часть источников задана в виде источников э. д. с., то эти источники необходимо заменить согласно правилу, изложенному в под-разд. 2.3, эквивалентными источниками тока. Эту замену можно произвести и мысленно, без изменения схемы цепи: оставить в ветви, содержащей источник э. д. с., имеющиеся в ней сопротивления, а при определении узловых токов учесть, что между узлами рассматриваемой ветви подсоединен источник тока, ток которого равен произведению э. д. с. на суммарную проводимость ветви.
В случае если какая-нибудь ветвь содержит идеальный источник э. д. с., τ. е. ее сопротивление равно нулю, и, следовательно, напряжение между двумя узлами задано, целесообразно в качестве базисного узла выбрать один из узлов данной ветви. В этом случае число неизвестных узловых напряжений и, следовательно, число узловых уравнений сократится на единицу.
Для пассивных цепей всегда справедливо равенство gkj = gjk а для активных цепей это равенство может оказаться несправедливым. Это будет рассмотрено в разд. 12.
Решив одним из известных методов систему уравнений (2.42), найдем потенциалы узлов, зная которые можно по закону Ома найти токи в ветвях.
Система уравнений узловых потенциалов (2.42) может быть записана в матричной форме:
||g|| ||φ||=||J||, (2.43)
где
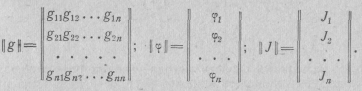
Решая это уравнение относительно матрицы ||φ||, получим
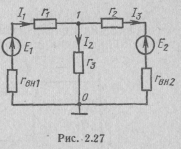 ||φ||=||g||-1||J||
||φ||=||g||-1||J||
При расчете электрических цепей методом узловых потенциалов целесообразно придерживаться следующего порядка:
1. Принять потенциал одного из узлов равным нулю, т. е. заземлить один из узлов и пронумеровать по порядку остальные узлы.
2. Вычислить узловые токи.
3. Определить собственные и взаимные проводимости узлов.
4. Составить и решить систему уравнений узловых потенциалов.
5. Найти токи в ветвях. Рассмотрим это на примере.
Пример 2.7.
Найти токи в ветвях электрической цепи, схема которой приведена на рис. 2.27, если дано: El=50 В; E2=10 В; rВН1=0,4 Ом; r1=3 Ом·, rВН2=1 Ом; r2=r3=2 Ом.
Решение.
Заземлим нижний узел, а верхний узел будем считать первым. Находим узловой ток верхнего узла
J1 = glE1 + g2E2 = 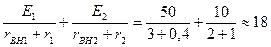 А.
А.
Собственная проводимость первого узла
gll =gl +g2 +g3 = 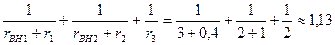 См.
См.
В рассматриваемом случае
gllφl =Jl,
откуда
φl=Jl/gll = 18/1,13  16 В.
16 В.
Токи в ветвях:
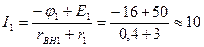 А;
А;
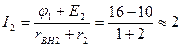 А;
А;
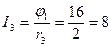 А.
А.
Одним из важных свойств метода узловых потенциалов, обеспечивающих ему наиболее широкое распространение для расчета электронных схем, является то, что матрица проводимостей сложной электрической цепи может быть получена путем простого сложения элементов матриц составляющих цепей, если потенциалы соответствующих узлов равны между собой.




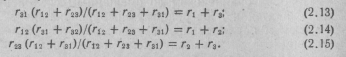
 и
и 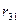 , найдем неизвестные сопротивления лучей эквивалент н ой звезды
, найдем неизвестные сопротивления лучей эквивалент н ой звезды 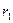 ,
, 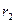 и
и 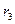 . Для этого из
. Для этого из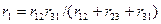 . (2.16)
. (2.16)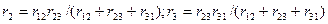 (2. 1 7)
(2. 1 7)
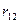 ,
, 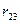 и
и 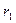 , r 2 и
, r 2 и 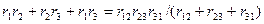 . (2. 1 8)
. (2. 1 8)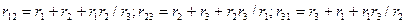 (2.19)
(2.19)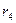 =5,5 Ом;
=5,5 Ом; 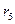 =7 О м;
=7 О м; 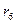 =2 О м. Определить ток в ветви с источником э. д. с. Е.
=2 О м. Определить ток в ветви с источником э. д. с. Е.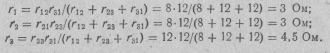

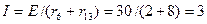 A.
A.
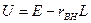 (2.20)
(2.20)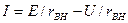 (2.21)
(2.21) (2.23)
(2.23)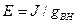 и g вн=1/ r вн. (2.24)
и g вн=1/ r вн. (2.24)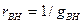 . (2.25)
. (2.25)
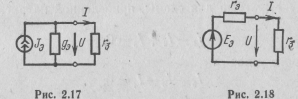
 Если сложная электрическая цепь имеет y узлов и в ветвей, а следовательно, в неизвестных токов, то необходимо составить и решить систему в линейно независимых уравнений. Покажем, что эти уравнения можно составить по первому и второму законам Кирхгофа.
Если сложная электрическая цепь имеет y узлов и в ветвей, а следовательно, в неизвестных токов, то необходимо составить и решить систему в линейно независимых уравнений. Покажем, что эти уравнения можно составить по первому и второму законам Кирхгофа.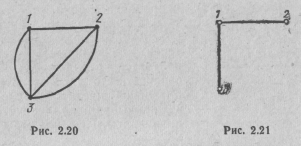
 5. Решить составленную систему уравнений относительно неизвестных токов. Если при этом некоторые токи получатся отрицательными, то это означает, что их действительные направления противоположны первоначально выбранным положительным направлениям. Поясним это на примере.
5. Решить составленную систему уравнений относительно неизвестных токов. Если при этом некоторые токи получатся отрицательными, то это означает, что их действительные направления противоположны первоначально выбранным положительным направлениям. Поясним это на примере.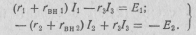
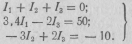
 Расчет сложных электрических цепей методом контурных токов сводится крешению системы уравнений, составленных только по второму закону Кирхгофа. Этих уравнений получается только n = в — (y — 1), т. е. на (y —1) меньше, чем при расчете цепи методом уравнений Кирхгофа. Это облегчает расчет сложных цепей.
Расчет сложных электрических цепей методом контурных токов сводится крешению системы уравнений, составленных только по второму закону Кирхгофа. Этих уравнений получается только n = в — (y — 1), т. е. на (y —1) меньше, чем при расчете цепи методом уравнений Кирхгофа. Это облегчает расчет сложных цепей. (2.31)
(2.31) или
или
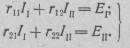 (2.34)
(2.34)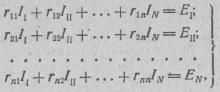 (2.35)
(2.35)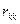 -собственное сопротивление k-го контура;
-собственное сопротивление k-го контура;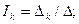 (2.36)
(2.36)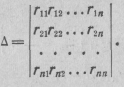
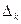 получается из определителя Δ путем замены k-го столбца свободными членами:
получается из определителя Δ путем замены k-го столбца свободными членами: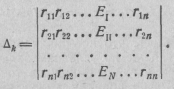
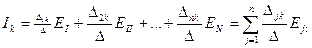 (2.37)
(2.37)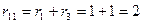 Ом;
Ом; 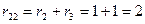 Ом.
Ом.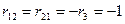 Ом.
Ом.
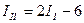 .
.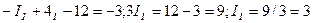 А;
А;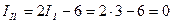
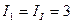 А;
А; 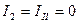 ;
; 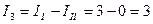 А
А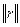
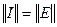 (2.38)
(2.38)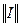 — матрица-столбец искомых контурных токов;
— матрица-столбец искомых контурных токов;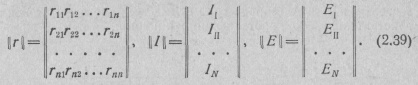

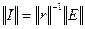
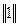 , то
, то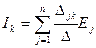 ,
,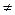 0, аостальные э. д. с. равными нулю, то получим частичный ток I " k, вызванный действием только э. д. с. Е2, и т. д. Алгебраическая сумма всех частичных токов даст действительный ток, протекающий в k-й ветви.
0, аостальные э. д. с. равными нулю, то получим частичный ток I " k, вызванный действием только э. д. с. Е2, и т. д. Алгебраическая сумма всех частичных токов даст действительный ток, протекающий в k-й ветви.
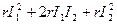 , а не
, а не 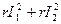 , как следовало бы из принципа наложения.
, как следовало бы из принципа наложения.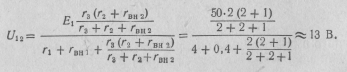
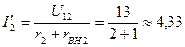 А.
А.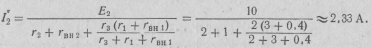
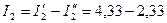 = 2 A направлен от узла 1 к узлу 2.
= 2 A направлен от узла 1 к узлу 2. Расчет сложных электрических цепей методом узловых потенциалов, или узловых напряжений, сводится к решению системы уравнений, составленных только по первому закону Кирхгофа. Из этих уравнений определяют напряжения в узлах схемы электрической цепи относительно некоторого базисного узла, потенциал которого принимают равным нулю, а токи в ветвях, соединяющих узлы, находят по закону Ома.
Расчет сложных электрических цепей методом узловых потенциалов, или узловых напряжений, сводится к решению системы уравнений, составленных только по первому закону Кирхгофа. Из этих уравнений определяют напряжения в узлах схемы электрической цепи относительно некоторого базисного узла, потенциал которого принимают равным нулю, а токи в ветвях, соединяющих узлы, находят по закону Ома.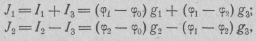

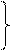 g11φ1 + g12φ2 = J1;
g11φ1 + g12φ2 = J1; g11φ1 + g12φ2 +... + g1nφn = J1;
g11φ1 + g12φ2 +... + g1nφn = J1;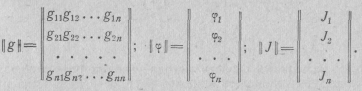
 ||φ||=||g||-1||J||
||φ||=||g||-1||J||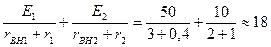 А.
А.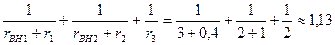 См.
См. 16 В.
16 В.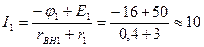 А;
А;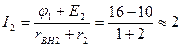 А;
А;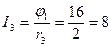 А.
А.


