К сожалению, далеко не всегда для алгоритма легко получить точную асимптотическую оценку, и приходится удовлетворяться оценками менее точными. Говорят, что f(n)=O(g(n)) (читается “О большое от g от n”), если найдётся такая константа c>0 и такое число n0, что f(n) 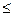 cg(n) для всех n
cg(n) для всех n 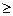 n0 (рис. 1.4,б). Функция g(n) представляет собой верхнюю асимптотическую оценку функции f(n) (где f(n) - например, время работы или другая характеристика алгоритма).
n0 (рис. 1.4,б). Функция g(n) представляет собой верхнюю асимптотическую оценку функции f(n) (где f(n) - например, время работы или другая характеристика алгоритма).
Зная оценку времени выполнения алгоритма T(n)=O(g(n)), мы можем сказать, что число операций алгоритма не превышает g(n), умноженному на некоторую константу. Однако, мы не знаем, действительно ли алгоритм будет выполнять столько операций – возможно, на самом деле их значительно меньше. Например, для алгоритма сортировки пузырьком, рассмотренного выше, можно сказать, что T(n)=O(n4). Однако, оценка T(n)=O(n3) характеризует алгоритм более точно, а T(n)=O(n2) - ещё точней (она совпадает с точной асимптотической оценкой). При анализе алгоритма нужно стремиться получить верхнюю оценку как можно ниже, тогда она будет иметь практическое значение.
Нижняя асимптотическая оценка Ω
Аналогично определяется нижняя асимптотическая оценка. Говорят, что f(n)=Ω(g(n)), если найдётся такая константа c>0 и такое число n0, что f(n) 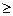 cg(n)) для всех n
cg(n)) для всех n 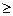 n0 (рис. 1.4в). Зная, что временя выполнения алгоритма T(n)=Ω(g(n)), мы можем сказать, что число операций алгоритма не меньше, чем g(n), умноженное на некоторую константу. Однако, данная характеристика не показывает, насколько действительно больше операций выполняет алгоритм в действительности. При анализе алгоритма нужно стремиться получить как можно более высокую нижнюю оценку.
n0 (рис. 1.4в). Зная, что временя выполнения алгоритма T(n)=Ω(g(n)), мы можем сказать, что число операций алгоритма не меньше, чем g(n), умноженное на некоторую константу. Однако, данная характеристика не показывает, насколько действительно больше операций выполняет алгоритм в действительности. При анализе алгоритма нужно стремиться получить как можно более высокую нижнюю оценку.
Примечание
Иногда нижнюю границу определяют несколько по-другому [3]: говорят, что f(n)=Ω(g(n)), если существует такая константа c, что f(n) 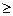 cg(n)) для бесконечно большого количества значений n. Например, алгоритм, который выполняет n операций для чётных значений n и n2 для нечётных, с этой точки зрения будет иметь максимальную нижнюю границу Ω(n2), тогда как для ранее данного определения – только Ω(n). Однако, для большинства практических алгоритмов оценки совпадают.
cg(n)) для бесконечно большого количества значений n. Например, алгоритм, который выполняет n операций для чётных значений n и n2 для нечётных, с этой точки зрения будет иметь максимальную нижнюю границу Ω(n2), тогда как для ранее данного определения – только Ω(n). Однако, для большинства практических алгоритмов оценки совпадают.
Точная асимптотическая оценка времени работы алгоритма находится где-то между его нижней и верхней оценками. В частности, несложно показать, что если T(n)=O(g(n)) и T(n)=Ω(g(n)), то T(n)=Θ(g(n)).
Исторически так сложилось, что верхняя асимптотическая оценка О была введена намного раньше оценок Θ и Ω (учебник Бахмана по теории простых чисел, 1892 год). Две последних асимптотических оценки были введены Дональдом Кнутом. Возможно, в связи с этим в литературе по программированию чаще используется оценка О, даже в тех случаях, когда она совпадает с точной асимптотической оценкой Θ. В дальнейшем изложении мы будем использовать все асимптотические оценки, отдавая предпочтение точной оценке Θ, если это не связано с чрезмерно большими вычислительными затратами.





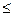 cg(n) для всех n
cg(n) для всех n 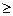 n0 (рис. 1.4,б). Функция g(n) представляет собой верхнюю асимптотическую оценку функции f(n) (где f(n) - например, время работы или другая характеристика алгоритма).
n0 (рис. 1.4,б). Функция g(n) представляет собой верхнюю асимптотическую оценку функции f(n) (где f(n) - например, время работы или другая характеристика алгоритма).


