Бинарный поиск в упорядоченном массиве

Он состоит в последовательном разделении упорядоченного массива пополам, при этом на каждом шаге можно определить, в какой из двух половин находится искомый элемент, сравнив искомый элемент и элемент, который находится в точке деления. При этом локализуется сначала половина массива, затем уже четверть массива и т. д. Процесс продолжается до тех пор, пока в массиве не останется один последний элемент. Если он совпадает с искомым значением, то поиск успешен, в противном случае имеем промах.

Данный алгоритм можно реализовать как итеративно, так и рекурсивно. На практике чаще используется более эффективный итеративный вариант, но рекурсивное решение является хорошей иллюстрацией идеи бинарного поиска.

// рекурсивный вариант функции,

// начальный вызов: seach_bin_r(a, 0, n-1, k);

item seach_bin_r(item a[], int l, int r, T_key k)

{ int m=(l+r)/2;

if (a[m].key==k) return a[m];//искомый элемент на границе

if (l==r)   return nullitem;//поиск закончен промахом

if (k<a[m].key) return seach_bin_r(a,l,m-1,k);

else       return seach_bin_r(a,m+1,r,k);

}

// нерекурсивный вариант функции бинарного поиска

item seach_bin(item a[], int n, T_key k)

{ int l=0, r=n-1;

while (l<=r)

{ int m=(l+r)/2;

if (k>a[m].key) l=m+1;

   else if (k<a[m].key) r=m-1;

   else return a[m];

}

return nullitem;

}

Максимальное количество делений массива пополам составляет ближайшее целое, большее log₂n, следовательно, асимптотическая оценка сложности поиска O(logn). Например, если в массиве 1000 элементов, то за 10 делений пополам мы уменьшим массив до одного элемента. Поиск может закончиться и раньше, если искомый элемент окажется граничным на каком-то промежуточном шаге.

Попробуем оценить, во что обходится поддержание массива в отсортированном виде. Ведь новый элемент уже нельзя вставить в конец массива, а удаляемый элемент нельзя заменить последним. Действительно, порядок временной сложности вставки становится O(n), время удаления также увеличивается, но асимптотическая оценка остается по-прежнему O(n) (сначала движемся по массиву вперед, чтобы найти нужный элемент, после этого продолжаем движение, перемещая каждый элемент влево).

На практике вопрос о применении данного алгоритма обычно решают путем сравнения количества операций поиска и операций обновления. Если данные обновляются редко, и размер массива велик, то бинарный поиск существенно ускорит производительность всего приложения в целом.

Бинарные деревья поиска

Проанализировав в целом реализацию поддержки поиска на основе линейной структуры, можно сделать вывод, что любой вариант включает функции с линейной временной сложностью алгоритма. При организации поиска на больших совокупностях данных стоит подумать об отказе от линейной структуры в пользу иерархической. Для этого есть весомые основания — в древовидной структуре, в отличие от линейной, путь от корня к любым данным не превышает высоты дерева, следовательно, имеется реальная возможность вообще избавиться от медленных операций с линейной сложностью.

Бинарное дерево поиска уже упоминалось в предыдущих главах. Напомним, что это упорядоченное бинарное дерево, для каждого узла которого выполняется условие — все левые потомки имеют ключи, меньшие, чем ключ узла, а правые — большие (возможно равные).

Анализ алгоритмов поиска, вставки и удаления

Поиск

На рис. 5.1 приведены четыре различных бинарных дерева одинаковой высоты, каждое из которых обладает свойством упорядоченности, поэтому принципиально может использоваться в качестве дерева поиска. При изображении деревьев здесь и далее в узлах будем показывать только значения ключей (целые положительные числа), этого вполне достаточно для того, чтобы понять суть дела.

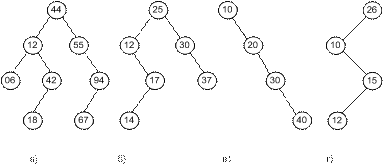
При достаточной плотности бинарного дерева поиска (рис.5.1,а) оно является очень удобной структурой быстрого поиска. Само название этого дерева, очевидно, связано с тем, что поиск нужного элемента можно выполнить кратчайшим путем. Двигаясь от корня к листьям и поворачивая при этом то вправо, то влево, мы в конце концов или найдем нужное значение ключа (попадание) или дойдем до пустой ссылки (промах). Путь, который был пройден до обнаружения попадания или промаха, назовем путем поиска.

Например, в дереве на рис.5.1,а значение 18 можно найти за 4 сравнения, при этом путь поиска пройдет через узлы с ключами 44 12 42 18 (последнее значение является искомым). Значение 55 будет найдено за 2 сравнения, а 44 (корень) будет обнаружено при первом же сравнении. При поиске значения 100 обнаружим промах за 3 сравнения, а при поиске числа 50 — промах за 2 сравнения.

При восьми узлах дерева это не так плохо, однако можно было бы получить и лучший результат (максимум 4 сравнения при 15 узлах), если бы бинарное дерево поиска оказалось полным (см. разд. 3.4). Действительно, высота полного бинарного дерева

h =log₂(n+1)-1,

т.е. в лучшем случае имеем логарифмическую сложность поиска, как для бинарного поиска в отсортированном массиве.

Для дерева на рис.5.1, б получаем результат похуже — для 6 узлов максимум 4 сравнения. И, наконец, на рис.5.1,в и 5.1,г представлены два самых худших варианта — вырожденные деревья, которые, по сути, ничем не отличаются от линейных списков, т. е. дают линейную сложность поиска.

Для того, чтобы избежать подобных крайне нежелательных ситуаций, на практике обычно используют так называемые сбалансированные деревья, высота которых специально поддерживается на своем нижнем уровне или близком к нему. Понятно, что сбалансированность дерева должна поддерживаться во время вставок и удалений элементов. Этому вопросу посвящен отдельный раздел, а сначала рассмотрим самые простые алгоритмы вставки и удаления, которые не гарантируют сбалансированной структуры дерева. Для нас они интересны тем, что с их помощью можно легко понять принципы работы с бинарными деревьями поиска, а затем использоваться их как основу алгоритмов для сбалансированных деревьев.

Для того, чтобы каждый раз отдельно не оговаривать лучший и худший случаи, будем оценивать сложность алгоритмов в зависимости от высоты дерева, а не от количества его узлов. Так, сложность алгоритма поиска можно оценить как

O(h), где h — высота бинарного дерева,

т. е. временная сложность поиска линейно зависит от высоты бинарного дерева поиска.

Вставка

Наиболее простым для реализации случаем вставки в бинарное дерево поиска является вставка каждого нового элемента в качестве листа дерева. В [13, 10] рассматривается алгоритм вставки нового элемента в корень, который также не гарантирует сбалансированности дерева, но приводит к тому, что последние добавленные элементы располагаются вблизи корня, следовательно, будут найдены быстрее (в некоторых задачах это важно). Вставка в корень будет рассмотрена немного позже, в данном разделе рассмотрим алгоритм вставки нового элемента в качестве листа.

Алгоритм вставки листа мало отличается от алгоритма поиска, поскольку сама вставка в уже найденную позицию сводится всего лишь к формированию нового элемента и присвоению значения соответствующей ссылке родителя. Поиск позиции для вставки представляет собой передвижение по пути поиска до обнаружения пустой ссылки.

Например, для того, чтобы вставить в дерево на рис.5.1,а новый узел с ключом 50, сначала перемещаемся по пути поиска. При этом обнаружим пустую ссылку на левого сына у узла с ключом 55. Именно в эту позицию и будет вставлен новый элемент (рис.5.2,а).

 

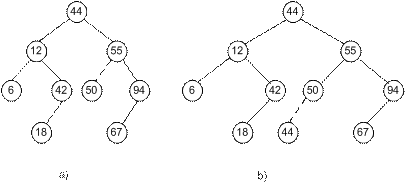
Рис.5.2. Добавление узлов в бинарное дерево поиска

Несколько слов о повторяющихся значениях ключей. Для приложений бинарных деревьев поиска это достаточно редкая ситуация, но принципиально она допустима. Попробуем добавить к дереву на рис.5.2,а еще один элемент с ключом 44. Но такой ключ уже есть у корня. Не обращая внимания на это совпадение, движемся дальше по правой ветви, следуя определению бинарного дерева поиска. Новое значение добавится в качестве левого сына только что добавленного листа со значением 50, оказавшись довольно далеко от корня. Можно сказать и точнее— повторяющееся значение будет крайним левым сыном в правом поддереве своего дубликата. Это наблюдение нам еще пригодится при реализации удаления.

Конечно, алгоритм поиска, который работает до первого совпадения, новый лист вообще никогда не найдет, поэтому для повторяющихся ключей этот алгоритм должен быть доработан.

А главный вывод, который можно сделать по алгоритму вставки — его временная сложность имеет тот же порядок, что и поиск. Временная сложность вставки, как и поиска, линейно зависит от высоты дерева.

Удаление

Удаление узлов выполняется несколько сложнее, чем поиск и вставка, поскольку новый узел можно всегда вставлять в качестве листа, но удалять приходится не только листья, но и внутренние узлы. Рассмотрим 3 основных ситуации.

1. Удаляется лист. Это самый простой случай, т. к. достаточно лишь обнулить соответствующую ссылку у родителя и, конечно, освободить память (это действие обязательно во всех случаях).

2. Удаляется внутренний узел, но имеющий только одно поддерево (левое или правое). Этот случай также особых проблем не представляет, т. к. единственное поддерево удаляемого узла подсоединяется к его родителю, и дерево не теряет своей упорядоченности.

3. Последний случай является самым сложным. У удаляемого внутреннего узла есть оба сына, например, из дерева на рис.5.3,а нужно удалить корень.

 

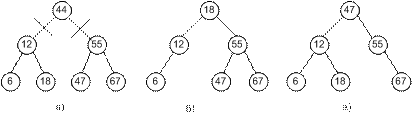
Рис.5.3. Удаления корня из бинарного дерева поиска (два варианта)

Ни один из сыновей удаляемого корня не сможет занять его место, не нарушив упорядоченности дерева. Но все же есть два варианта решения этой задачи, изображенные на рис.5.3,б и 5.3,в. В первом случае это самый последний правый сын из левого поддерева, во втором, наоборот, самый последний левый сын, но из правого поддерева. Оба решения вполне логичны, на самом деле, это два самых близких значения к ключу корня (одно немного меньше, другое немного больше, а при наличии повторяющихся значений вторым способом будет найден дубликат). При реализации для определенности можно следовать любому из двух вариантов.

Несмотря на разветвленную логику алгоритма удаления, количество перемещений по дереву по-прежнему не превышает его высоту. Это значит, что  мы опять имеем линейную зависимость от высоты дерева.

Итак, последний вывод — бинарное дерево поиска с хорошей степенью плотности позволяет полностью избежать медленных операций с линейной сложностью от количества узлов дерева, при этом все операции имеют линейную сложность от высоты.

 Теперь можно перейти к реализации функций для работы с бинарным деревом поиска.