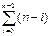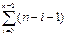Время выполнения в худшем и среднем случае

Существуют алгоритмы, время работы которых зависит только от размера входных данных, но не зависит от самих данных (например, поиск суммы элементов заданного массива). Для таких алгоритмов можно вывести аналитическую зависимость времени выполнения от размера задачи T(n).

Однако большинство алгоритмов содержит ветвления, поэтому время их выполнения зависит не только от количества входных данных, но и от самих значений этих данных. Для сравнения таких алгоритмов обычно определяют время их выполнения для наихудшего или для среднего случая (время выполнения в наилучшем случае обычно представляет меньший интерес). В связи с этим говорят о времени выполнения алгоритма в наихудшем случае (т.е. максимальное время выполнения по возможным входным данным) и о времени выполнения в среднем. Время выполнения в среднем можно определить по-разному:

· среднее время работы алгоритма по всем возможных вариантам входных данных;

· ожидаемое время его работы по всем возможным вариантам входных данных с учетом вероятности их появления

Недостатки есть и у того, и у другого способов:

· Первый способ не учитывает, что в реальных задачах данные часто распределены неравномерно.

· При втором способе получается, что мы анализируем алгоритм не в общем виде, а применительно к некой предполагаемой области, для которой можно определить вероятности появления различных входных данных.

Чаще всего при анализе времени работы алгоритма ограничиваются наихудшим случаем. Причины этого в следующем:

· Время выполнения в наихудшем случае обычно найти гораздо проще, чем в среднем.

· Зная верхнюю границу, мы можем быть уверены, что алгоритм не будет работать дольше ни на каких входных данных.

· Для многих алгоритмов плохие случаи (или близкие к ним) могут происходить очень часто.

· Зачастую «средний случай» почти так же плох, как и наихудший. Например, сортировка вставками или любой другой квадратичный алгоритм сортировки.

Тем не менее, время выполнения в среднем также иногда анализируют – например, для тех алгоритмов, где оно существенно отличается от наиухудшего, и при этом вероятность появления «плохих» входных данных достаточно мала (алгоритм быстрой сортировки Хоара и др.)

Для примера найдём время выполнения алгоритма сортировки массива методом пузырька для худшего случая. Сортировка методом пузырька выполняется следующим образом. Двигаясь от конца массива к началу, мы на каждом шаге сравниваем очередные два соседних элемента. Если первый элемент больше второго, то меняем их местами. Таким образом, после первого прохода по массиву самый маленький элемент поднимется на самый верх массива и займёт нулевую позицию. Второй цикл сортировки выполняется для оставшейся части массива (без первого элемента), в результате следующий по величине элемент окажется в первой позиции массива, и т.д.

Отметим около каждой строки её стоимость (число операций) и число раз, которое эта строка выполняется.

void bubble(int *a, int n) { int i,j,temp; 1 for(i=0; i<n-1; i++)   2 for (j=n-1; j>i;j--)      3      if (a[j-1]>a[j])   4   { temp=a[j-1];   5     a[j-1]=a[j];   6     a[j]=temp;      }  }

стоимость     c1   c2   c3   c4   c5   c6

Число раз     N

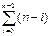
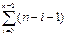
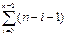
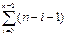
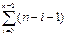
В худшем случае массив изначально упорядочен по убыванию, и условие в строке 3 всегда истинно, в результате чего строки 4-6 всегда выполняются.

Общее время работы получается следующим:

 T(n)=c₁n+c₂ 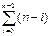+(c₃+c₄+c₅+c₆) =

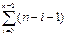=c₁n+c₂ 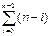+(c₃+c₄+c₅+c₆) 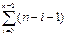= (с₂+c₃+c₄+c₅+c₆)n²/2+(c₁+(c₂-c₃-c₄-c₅-c₆)/2)n-c₂

Как видим, даже для сравнительно несложного алгоритма расчет получается весьма трудоемким.