В большинстве случаев нет необходимости находить точное число действий, выполняемых алгоритмом. Интерес представляет общий вид зависимости времени работы алгоритма от размера входных данных, стремящегося в пределе к бесконечности – т.е. асимптотическая временная сложность ( аналогично можно рассматривать асимптотическую пространственную сложность). Так, для рассмотренного выше примера сортировки методом пузырька T(n) имеет вид an2+bn+c. Однако, можно огрубить данную зависимость ещё сильней и сказать, что T(n) имеет порядок n2. Слагаемые низшего порядка не учитываются, поскольку при больших входных данных они играют незначительную роль. Мультипликативную константу при старшем члене также обычно опускают. Причины этого в следующем:
Мультипликативная константа может зависеть от разных факторов, не связанных непосредственно с алгоритмом – например, от мастерства программиста, качества компилятора и других факторов.
Для подавляющего большинства известных алгоритмов эта константа находится в разумных пределах. Это означает, что алгоритмы, которые более эффективны асимптотически, оказываются более эффективными и при тех сравнительно небольших размерах входных данных, для которых они используются на практике.
Для примера рассмотрим два алгоритма сортировки. Пусть первый алгоритм выполняет сортировку массива из n чисел за 2·n2 операций, второй – за 100·n·log2n операций. Хотя при совсем маленьких значениях n первый алгоритм работает быстрее, с увеличением n второй алгоритм становится значительно более эффективным. Так, при n=10000 второй алгоритм работает в 15 раз быстрее первого, при n=100000 – в 120 раз, а при n=1000000 – более чем в 1000 раз.
Примечание
Асимптотические оценки всё-таки достаточно грубо характеризуют алгоритм, и в ряде случаев при анализе алгоритма (особенно при сравнении алгоритмов одного порядка сложности) стремятся получить и более точные оценки, например, сколько раз выполнится та или иная специфическая операция. Так, для алгоритмов сортировки часто рассматриваются такие характеристики, как число сравнений элементов и число замен.
Рассмотрим теперь данные понятия более строго, используя асимптотические обозначения, принятые в математике.
Точная асимптотическая оценка Θ
Запись f(n)=Θ(g(n)) (читается как “тэта от g от n”), где g(n) - некоторая функция, означает следующее: найдутся такие константы c1,c2>0 и такое число n0, что c1g(n) 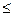 f(n)
f(n) 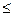 c2g(n) для всех n
c2g(n) для всех n 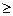 n0. Функция g(n) в этом случае является асимптотически точной оценкой для f(n). На рис. 1.4а. показана иллюстрация данного определения.
n0. Функция g(n) в этом случае является асимптотически точной оценкой для f(n). На рис. 1.4а. показана иллюстрация данного определения.
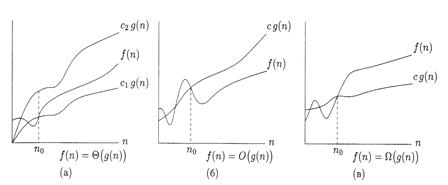
Рис.1.4. Иллюстрации к определениям f(n)=Θ(g(n)), f(n)=O(g(n), f(n)=Ω(g(n)) (рисунок взят из [10]).
Здесь и далее предполагается, что функции f и g неотрицательны по крайней мере для достаточно больших n.
Пример 1. Покажем, что (n+1)2=Θ(n2). Нам нужно найти такие константы c1 и c2, что для всех достаточно больших n будут выполняться неравенства: c1n2 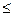 (n+1)2, (n+1)2
(n+1)2, (n+1)2 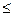 c2n2.
c2n2.
Возьмём c1=1, тогда первое неравенство, очевидно, верно для всех n 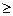 1. Возьмём c2=4. Тогда имеем:
1. Возьмём c2=4. Тогда имеем:
(n+1)2 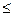 4n2
4n2  (n+1)2-4n2
(n+1)2-4n2 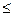 0
0  (n+1-2n)(n+1+2n)
(n+1-2n)(n+1+2n) 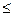 0
0  (1-n)(3n+1)
(1-n)(3n+1) 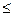 0.
0.
Полученное неравенство также выполняется для всех n 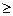 1. Таким образом, действительно (n+1)2=Θ(n2).
1. Таким образом, действительно (n+1)2=Θ(n2).
Пример 2. Покажем, что 3n 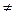 Θ(2n). Для этого убедимся, что неравенство 3n
Θ(2n). Для этого убедимся, что неравенство 3n 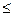 c22n не может выполняться для всех достаточно больших n ни для какого фиксированного c2. Имеем:
c22n не может выполняться для всех достаточно больших n ни для какого фиксированного c2. Имеем:
3n 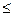 c22n
c22n  (3/2)n
(3/2)n 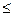 c2.
c2.
Какая бы большая ни была константа c2, выражение (3/2)n при достаточно больших n всё равно превысит её. Отсюда следует, что 3n 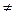 Θ(2n).
Θ(2n).
Используя аналогичные рассуждения, легко показать, что точная асимптотическая оценка времени выполнения рассмотренного выше алгоритма сортировки пузырьком T(n)= Θ (n2) в наихудшем случае.





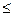 f(n)
f(n) 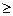 n0. Функция g(n) в этом случае является асимптотически точной оценкой для f(n). На рис. 1.4а. показана иллюстрация данного определения.
n0. Функция g(n) в этом случае является асимптотически точной оценкой для f(n). На рис. 1.4а. показана иллюстрация данного определения.
 (n+1)2-4n2
(n+1)2-4n2 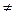 Θ(2n). Для этого убедимся, что неравенство 3n
Θ(2n). Для этого убедимся, что неравенство 3n 

