Явления переноса. Внутреннее трение (вязкость). Закон Ньютона. Коэффициент динамической вязкости идеального газа.

Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества. Выравнивание неоднородностей приводит к возникновению явления переноса.

Явления переноса в газах и жидкостях состоят в том, что в этих веществах возникает упорядоченный, направленный перенос массы (диффузия), импульса (внутренняя энергия) и внутренней энергии (теплопроводность). При этом в газах нарушается полная хаотичность движения молекул и распределение молекул по скоростям.

Вя́зкость (вну́треннее тре́ние) — свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

В газах внутреннее трение обусловлено переносом импульса, в жидкостях – взаимодействием молекул. Явление вязкости или внутреннего трения наблюдается, когда соприкасающиеся слои жидкости или газа движутся с различными скоростями. Если │ 2│>│ 1│, то для поддержания такого движения нужно приложить силуF в направлении скорости движения, равную силе внутреннего трения. Величина этой силы равна:│F │=s*η*(│ 2- 1│)/∆z и называется законом Ньютона для силы внутреннего трения.

Коэффициент динамической вязкости идеального газа:

Билет №15

Вопрос №1

Динамика гармонических колебаний. Дифференциальное уравнение гармонических колебаний. Энергия гармонических колебаний. Примеры свободных колебательных систем: пружинный маятник, математический маятник, физический маятник.

Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Уравнение гармонических колебаний имеет вид x=ACos(wt+ф) или x=ASin(wt+ф) где x - смещение колеблющейся величины от положения равновесия.

Дифференциальное уравнение гармонических колебаний

Составим дифференциальное уравнение гармонических колебаний на примере пружинного маятника Сначала запишем уравнении динамики 2ой закон Ньютона: 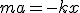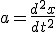И теперь: Делим на m и обозначаем : 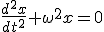Это уравнение решается.

Энергия гармонических колебаний

По определению кинетическая энергия тела массой m, движущегося со скоростью равна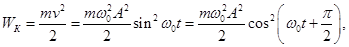

Потенциальная энергия равна

Полная энергия равна

Пружинный маятник - это груз массой m, закрепленный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы Fупр= - k x, где k - коэффициент упругости, в случае пружины называемый жесткостью. Уравнение движения маятника или . Из приведенных выражений следует, что пружинный маятник совершает гармо­нические колебания по закону х = A cos (w0 t + j), с циклической частотой и периодом

Математический маятник - материальная точка, совершающая под действием силы тяжести колебания вдоль дуги окружности, расположенной в вертикальной плоскости. Период длина нити

Физический маятник - абсолютно твердое тело, совершающее малые колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через его центр тяжести.

Билет №15

Вопрос №2

Рапределение молекул по кинетическим энергиям ɛ их поступательного движения. График f(). Вычисления вероятнейшей ɛвер и средней <ɛ> кинетической энергии поступательного движения молекул.

Функция распределения по значениям кинетической энергии поступательного движения молекул, характеризующая вероятность попадания значений кинетической энергии в интервал: . Приравняв вероятности или 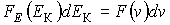, и используя подстановку и , имеем: 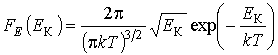. Это распределение справедливо только для равновесного состояния термодинамической системы. Вследствие достаточно общего метода его получения, оно применимо не только для газов, но и для любых систем, движение микрочастиц которых описывается уравнениями классической механики.

Вероятнейшее значение Определим производную функции 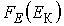и приравняем её нулю: .Тогда имеем выражение для наиболее вероятного значения кинетической энергии :.

Среднее значение: т.к. i=3, то <E>=3/2*k*T

Билет №16

Вопрос №1