Идеальный газ - газ, молекулы которого пренебрежительно малого размера и между которыми отсутствуют силы взаим-ия.
Если газ поместить в поле внешних сил, то концентрация молекул и др. хар-ки связанные с конц-ией изменяться.
Будем считать что все силы, действующие на молекулы консервативны и во всех точках расм. объема одинаково направлены.
dp=FnSdz/S=Fndn; где n-концентрация молекул; F-сила, дейст-ая на одну молекулул сое с координатой z.
F(z)=-dU(z)/dz dP=-n(dU/dz)/dz=-ndU т. к. газ идеальный P=nkT, тогда dp=kTdn; -ndU=kTdn; dn/n=-dU/kT; ln n = -U/kT+ln c:
ln n/c=-UkT n=c*exp(-U/kT); no=c n= no exp(-U/kT);- это выражение связывает конц-ию n(z) молекул идеального газа с потенциальной энергией U(z) одной молекулы при T=const во всех слоях и наз-ся формулой распределения Больцмана.
Поскольку концентрация молекул и давление связаны прямой пропорциональной зависимостью, то давление можно записать аналогично p(z)=poexp(-U(z)/kT)
Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.
Для идеального газа, имеющего постоянную температуру  и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения
и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения  одинаково), барометрическая формула имеет следующий вид:
одинаково), барометрическая формула имеет следующий вид:
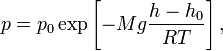 где
где  — давление газа в слое, расположенном на высоте
— давление газа в слое, расположенном на высоте  ,
, 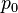 — давление на нулевом уровне (
— давление на нулевом уровне ( ),
),  — молярная масса газа,
— молярная масса газа, 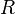 — универсальная газовая постоянная,
— универсальная газовая постоянная,  — абсолютная температура.
— абсолютная температура.
Билет№3
Вопрос №1
Механическая система частиц. Понятие о состоянии частицы и системы частиц в классической механике. Внешние и внутренние силы. Замкнутая система. Центр масс механической системы и закон его движения.
Системой мат. точек (частиц) – пространственная совокупность мат. точек, связанных между собой силами или имеющих возможность сталкиваться между собой. При этом каждое тело системы может взаимодействовать, как с телами, принадлежащими этой системе, так и с телами, на входящими в нее.
Силы, действующие между телами системы, называются внутренними силами. Силы, действующие на тела системы со стороны тел, не входящих в данную систему, называются внешними силами.
Система тел наз. замкнутой, если внешние силы отсутствуют или их сумма равна нулю.
Центром масс (центр инерции) механической системы наз. т. С, радиус-вектор который задан ур-ем

Дифференциальное уравнение движением центра масс:

Теорема о движении центра масс: центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему. Скорость движения центра масс замкнутой системы остается постоянной.
Билет №3
Вопрос №2
Понятие о релаксационных процессах и времени релаксации. Явление переноса. Размеры и сечение столкновения молекул. Число столкновений и длина свободного пробега молекулы. Их зависимость от давления, температуры и размеров молекул.
Процесс перехода системы из неравновесного состояния в равновесное наз. процессом релаксации.
Время затрачиваемое на такой переход- время релаксации- время за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в e раз.
Релаксация осущ. за счет так наз. явлении переноса, приводящих к выравниванию неоднородности. Явление переноса - необр. процесс. К ним относятся: Диффузия, теплопроводность, вязкость. Явления переноса хар. для идеального газа (газ, молекулы которого двигаются от соударения до соударения без взаимодействия в первом приближении).
Будем представлять молекулы в виде твердых шариков со вполне определенным диаметром.
Мин. расстояние d между центрами сблизившихся при соударении молекул наз. эффективным диаметром молекулы.
Величина σ=πd^2(м^2) наз=ся эффективным сечением столкновения.
Число соударений в единицу времени ν=(√2)πd^2<V>n=(√2)σ <V>n
Средняя длина свободного пробега молекулы: λ=<V>/ν=1/(√2)σn
При этом длина свободного пробега не зависит от температуры, т к ни одна величина от Т не зависит.
Чем меньше температура (меньше скорость движения молекул) тем больше эффективное сечение и тем меньше длина свободного пробега.
Билет№4
Вопрос №1





 и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения
и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения  одинаково), барометрическая формула имеет следующий вид:
одинаково), барометрическая формула имеет следующий вид: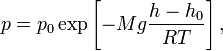 где
где  — давление газа в слое, расположенном на высоте
— давление газа в слое, расположенном на высоте  ,
, 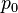 — давление на нулевом уровне (
— давление на нулевом уровне ( ),
),  — молярная масса газа,
— молярная масса газа, 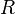 — универсальная газовая постоянная,
— универсальная газовая постоянная, 




