Метастабильное состояние — состояние квазиустойчивого равновесия физической системы, в котором система может находиться длительное время.
Метастабильные состояния соответствуют одному из минимумов термодинамического потенциала системы при заданных внешних условиях. Устойчивому (стабильному) состоянию отвечает самый глубокий минимум. Однородная система в метастабильном состоянии удовлетворяет условиям устойчивости равновесия термодинамического Cр>Cv>0, (dP/dV)_T<0, относительно малых возмущений физических параметров (энтропии, плотности и др.). При достаточно больших возмущениях система переходит в абсолютно устойчивое состояние.
Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением  , где
, где  — удельная теплота фазового перехода,
— удельная теплота фазового перехода,  — изменение удельного объёма тела при фазовом переходе.
— изменение удельного объёма тела при фазовом переходе.
Билет №20
Вопрос №1
Понятие о затухающих колебаниях. Дифференциальное уравнение затухающих колебаний. Зависимость амплитуды колебаний от времени. Коэффициент затухания. Логарифмический декремент затухания.
Механическими колебаниями называют движения тел, повторяющиеся точно или приблизительно через одинаковые промежутки времени.
Свободные механические колебания всегда оказываются затухающими, те колебаниями с убывающей амплитудой.
Диф. Уравнение затухающих колебаний:  , где
, где 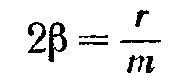 , а
, а 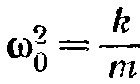 .
.
Амплитуда колебаний постепенно уменьшается, и через некоторое время после начала колебаний становится равной нулю.
Коэффициент затухания – скорость затухания колебаний, определяемая величиной β=r/2m. Коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшилась в е раз. (βτ=1, где τ, время, за которое амплитуда уменьшится в е раз.)
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно a(t) / a(t+T)= eβT. Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания: Λ=lna(t)/a(t+T)=βT
Последнюю величину обычно используют для характеристики затухания колебаний. Выразив β через λ и Т в соответствии с (73.12), закон убывания амплитуды можно записать в виде а = а0 е -λ/T· tЗа время т, за которое амплитуда уменьшается в е раз, система успевает совершить Ne = τ/Т колебаний.Из условия е -λ·τ/T =е-1 получается, что λ·τ/T = λNe = 1.Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.
Билет №20
Вопрос №2!!!!!!!





 , где
, где  — удельная теплота фазового перехода,
— удельная теплота фазового перехода,  — изменение удельного объёма тела при фазовом переходе.
— изменение удельного объёма тела при фазовом переходе. , где
, где 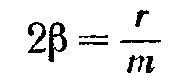 , а
, а 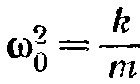 .
.


