Билет№1
Вопрос №1
Предмет динамики. Инерциальные системы отсчета. 1 закон Ньютона. Масса. 2 закон Ньютона. Принцип независимости действия сил. Уравнения движения в векторной и координатной формах.
Динамика занимается изучением движения обладающих массой тел под действием приложенных к ним сил.
Инерциальная СО – система координат, жестко связанная со свободной мат. точкой.. Любая сис-ма отсчета, движущаяся относительно некоторой инерц. сис-мы прямолинейно и равномерно, будет также инерциальной.
1-й з-н Ньютона: свободная мат. точка движется равномерно и прямолинейно, если на нее не действуют никакие силы.
Количественная мера механического воздействия на тело со стороны других тел или силового поля наз. силой.
Масса - физическая величина тела, являющаяся мерой его инерционных и гравитационных свойств.
2-й з-н Ньютона: Изменение скорости движения тела пропорционально приложенной силе и происходит по направлению той прямой, по которой действует сила.
В векторной форме: F=ma=m*dv/dt
при m=const: d(mv)/dt=dP/dt =F
В координатной форме:  ,
, 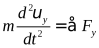 ,
, 
Принцип независимости: Если на тело действует сразу несколько сил то ускорение которое приобретается телом от каждой силы не зависит от того действует ли на это тело другие силы или нет.
Уравнения движения в векторной и координатной формах: r=ix+jy+kv; x=x(t), y=y(t), z=z(t)
Билет№1
Вопрос №2
Билет №2
Вопрос №1
Система отсчета. Координатная и векторная формы описания движения материальной точки. Перемещение, скорость, ускорение и их проекции на координатные оси. Криволинейное движение. Нормальное и тангенсальное ускорения.
Система отсчета- система координат, тесно связанная с 1 телом или с группой тел (если их взаимное положение не меняется).
Уравнения движения в векторной и координатной формах: r=ix+jy+kv; x=x(t), y=y(t), z=z(t)
Мат. точка-тело размерами формой которого в условиях данной задачи можно пренебречь.
Перемещение-вектор, направленный от начальной точки к конечной, численно равный расстоянию между этими точками.
Траектория- линия которую описывает точка при своем движении
Скорость- векторная величина, хар. быстротой перемещения частицы по траектории и направлению, в котором движется частица в каждый момент времени.<V>=∆r/∆t;
 ; V= iVх+jVу+kVz
; V= iVх+jVу+kVz
Ускорение- векторная величина, хар. изменения скорости мат. точки с течением времени.  a=iaх+jaу+kaz
a=iaх+jaу+kaz
Криволинейное движение - это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу).
 У скорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
У скорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
Изменение величины скорости за единицу времени – это тангенциальное ускорение:
 или
или  , где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно.
, где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно.
Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение - это изменение скорости по направлению за единицу времени: 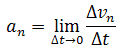
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Полное ускорение при равнопеременном криволинейном движении тела равно:

Билет №2
Вопрос №2
Билет№3
Вопрос №1
Билет №3
Вопрос №2
Понятие о релаксационных процессах и времени релаксации. Явление переноса. Размеры и сечение столкновения молекул. Число столкновений и длина свободного пробега молекулы. Их зависимость от давления, температуры и размеров молекул.
Процесс перехода системы из неравновесного состояния в равновесное наз. процессом релаксации.
Время затрачиваемое на такой переход- время релаксации- время за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в e раз.
Релаксация осущ. за счет так наз. явлении переноса, приводящих к выравниванию неоднородности. Явление переноса - необр. процесс. К ним относятся: Диффузия, теплопроводность, вязкость. Явления переноса хар. для идеального газа (газ, молекулы которого двигаются от соударения до соударения без взаимодействия в первом приближении).
Будем представлять молекулы в виде твердых шариков со вполне определенным диаметром.
Мин. расстояние d между центрами сблизившихся при соударении молекул наз. эффективным диаметром молекулы.
Величина σ=πd^2(м^2) наз=ся эффективным сечением столкновения.
Число соударений в единицу времени ν=(√2)πd^2<V>n=(√2)σ <V>n
Средняя длина свободного пробега молекулы: λ=<V>/ν=1/(√2)σn
При этом длина свободного пробега не зависит от температуры, т к ни одна величина от Т не зависит.
Чем меньше температура (меньше скорость движения молекул) тем больше эффективное сечение и тем меньше длина свободного пробега.
Билет№4
Вопрос №1
Билет №4
Вопрос №2
Распределение Максвелла. Функция распределения молекул по абсолютным значениям скорости(f(v)). График f(v). Вычисление вероятнейшей Vвер, средней арифметической <v> и средней квадратичной vср.кв. скоростей молекул идеального газа.
распределение Максвелла.
Распределение Максвелла по скоростям: 
Распределение Максвелла по компонентам скорости ( ):
): 
Распределение Максвелла по абсолютным значениям скорости: 
Наиболее вероятная скорость,  — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению
— вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению  . Чтобы найти её, необходимо вычислить
. Чтобы найти её, необходимо вычислить  , приравнять её нулю и решить относительно
, приравнять её нулю и решить относительно 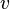 :
: 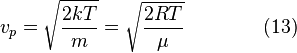
Средняя скорость 
Среднеквадратичная скорость 
Подставляя  и интегрируя, мы получим
и интегрируя, мы получим 
Билет №5
Вопрос №1
Потенциальные кривые. Потенциальные кривые межмолекулярного взаимодействия (потенциал Ленарда- Джонса) и межатомного взаимодействия.
График зависимости потенциальной энергии от некоторого аргумента называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.
Билет№5
Вопрос №2
Билет №6
Вопрос №1
Билет №6
Вопрос №2
Предмет молекулярной физики. Статистический и термодинамический методы. Основные положения МКТ. Размеры и сечение столкновения молекул. Число столкновений и длина свободного пробега молекул. Число Ван-дер-Ваальса. Число Кнудсена. Идеальный газ.
Молек.ф. представляет собой раздел ф., изучающий строение и свойства вещ-ва, исходя из молекул.-кинет. представлений. Согласно этому любое тело-состоит из большого кол-ва очень маленьких обособленных частиц. Они находятся в хаотическом движении. Его интенсивность зависит от температуры вещ-ва. Док-вом этого служит броуновское движение. МКТ ставит себе целью истолковать свойства тел наблюдаемые на опыте (давление, температуру) как суммарный результат действия молекул.
Статистический метод-использую лишь средними величинами, кот. хар. движение огромной совокупности частиц. Изучением различных св-в тел и изменений сост. в-ва занимается термодинамика.
Положения МКТ: 1) все тела состоят из большого числа мельчайших частиц.2) эти частицы непрерывно и хаотически движутся. 3)частицы взаимодействуют друг с другом. молекулы газа находясь в тепловом движении непрерывно сталкиваются друг с другом.
Будем представлять молекулы в виде твердых шариков со вполне определенным диаметром.
Мин. расстояние d между центрами сблизившихся при соударении молекул наз. эффективным диаметром молекулы.
Величина σ=πd^2(м^2) наз=ся эффективным сечением столкновения.
Число соударений в единицу времени ν=(√2)πd^2<V>n=(√2)σ <V>n
Средняя длина свободного пробега молекулы: λ=<V>/ν=1/(√2)σn
Число Ван-дер-Ваальса Na = (6,022045±0,000031)*10 23
Число Кнудсена (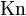 ) — один из критериев подобия движения разрежённых газов:
) — один из критериев подобия движения разрежённых газов:

Идеальным называется газ, молекулы которого имеют пренебрежимо малый собственный объем и не взаимодействуют друг с другом на расстоянии.
Билет №7
Вопрос №1
Билет №7
Вопрос №2
Явления переноса. Перенос на 3 уровнях: макроскопическом, молекулярном и квантовом. Перенос энергии, импульса и массы на молекулярном уровне. Теплопроводность. Закон Фурье. Коэффициент теплопроводности идеального газа.
Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества. Выравнивание неоднородностей приводит к возникновению явления переноса.
Явления переноса в газах и жидкостях состоят в том, что в этих веществах возникает упорядоченный, направленный перенос массы (диффузия), импульса (внутренняя энергия) и внутренней энергии (теплопроводность). При этом в газах нарушается полная хаотичность движения молекул и распределение молекул по скоростям.
Перенос на 3 уровнях:
Квантовый уровень – тепловое излучение– перенос тепла с помощью электромагнитных волн, источниками которых являются колебания заряженных частиц в рассматриваемом объеме. Все тела способны излучать энергию, которая поглощается другими телами и снова превращается в тепло. Таким образом, осуществляется лучистый теплообмен; он складывается из процессов лучеиспускания и лучепоглощения
2. Молекулярный уровень – теплопроводность – представляет собой перенос тепла вследствии беспорядочного (теплового) движения микрочастиц, непосредственно соприкасающихся друг с другом. Это движение может быть либо движением самих молекул (газы, капельные жидкости), либо колебанием атомов (в кристаллической решетке твердых тел), или диффузией свободных электронов (в металлах). В твердых телах теплопроводность является обычно основным видом распространения тепла.
3. Макроуровень – конвекция – называется перенос тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости. Перенос тепла возможен в условиях естественной, или свободной конвекции, обусловленной разностью плотностей в различных точках объема жидкости (газа), возникающей вследствие разности температур в этих точках или в условиях вынужденной конвекции при принудительном движении всего объема жидкости, например в случае перемешивания ее мешалкой.
Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела
Закон Фурье: поток теплоты пропорционален градиенту температуры. 
Коэффициент теплопроводности газов 
Билет №8
Вопрос №1
Билет №8
Вопрос №2
Термодинамический метод в физике. Параметры, характеризующие макросистемы. Равновесное состояние. Внутренняя энергия. Работа термодинамической системы. Количество теплоты. Теплоемкость системы. Удельная и молярная теплоемкости.
Задачей термодинамического метода изучения состояний макроскопических систем является установление связей между непосредственно наблюдаемыми величинами, такими, как давление, объем, температура, концентрация раствора, напряженность электрического или магнитного поля, световой поток и т.д. Термодинамический метод обладает большей общностью, отличается простотой и ведет, после ряда простых математических процедур, к решению целого ряда конкретных задач, не требуя никаких сведений о свойствах атомов или молекул.
Макросистемой называется система, состоящая из большого количества частиц. Состояние макросистемы характеризуют величинами, которые называются термодинамическими параметрами (давление р, объем V, температура Т и т.д.)
Состояние системы является равновесным, если все параметры ее имеют определенные и постоянные значения при неизменных внешних условиях.
Внутренняя энергия – это энергия частиц, из которых состоит вещество. Она включает в себя: суммарную кинетическую энергию хаотического движения молекул в Ц–системе; собственную потенциальную энергию взаимодействия всех молекул; внутреннюю энергию самих молекул, атомов и
В термодинамике работа - это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы.
Рассмотрим цилиндр с идеальным газом, который находится под подвижным поршнем. Пусть внешняя сила, действующая на поршень, перемещает его из состояния 1 в состояние 2.
Работа силы равна  . Со стороны газа на поршень действуют сила, равная произведению давлению газа на поршень и площадь сечения поршня
. Со стороны газа на поршень действуют сила, равная произведению давлению газа на поршень и площадь сечения поршня  . Подставив вторую формулу в первую, получим
. Подставив вторую формулу в первую, получим  .
.
Количество теплоты — энергия, которую получает или теряет тело при теплопередаче.
Нагрев/охл. Q = cmΔT, где с - удельная теплоемкость [Дж/кг·К], m - масса тела [кг], ΔT - изменение температуры [К]
Парообр./конденс. Q = Lm, где L - удельная теплота парообразования [Дж/кг], m - масса тела [кг]
Плав./крист. Q = λm, где λ (лямбда) - удельная теплота плавления [Дж/кг], m - масса тела [кг]
Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δ Q, полученного телом, к соответствующему приращению его температуры δ T [1]:

Удельная теплоемкость вещества - величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:  , Дж/(кгК). (9)
, Дж/(кгК). (9)
Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К: 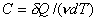 , Дж/(мольК). (10)где n=m/M - количество молей вещества.
, Дж/(мольК). (10)где n=m/M - количество молей вещества.
Билет№9
Вопрос №1
Билет №9
Вопрос №2
1 Начало термодинамики и его применение к изопроцессам в идеальных газах. Теплоемкости при постоянном объеме и давлении. Энтальпия.
Сущность первого начала термодинамики заключается в следующем: термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии.
При сообщении термодинамической системе некоторого количества теплоты Q в общем случае происходит изменение внутренней энергии системы D U и система совершает работу А:
Является определением изменения внутренней энергии системы (D U), так как Q и А — независимо измеряемые величины.
Первое начало термодинамики:
при изобарном процессе 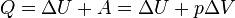
при изохорном процессе постоянный объем ( )
) 
при изотермическом процессе 

Молярная теплоемкость при постоянном объеме  ,
, 
молярная теплоемкость газа при постоянном объеме —

Если газ нагревается при постоянном давлении, то согласно первому закону термодинамики
 где
где 
Тогда теплоемкость газа при постоянном давлении 
Молярная теплоемкость при постоянном давлении: 
Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц. Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении.
H=E=U+pV
Билет №10
Вопрос №1
Билет №10
Вопрос №2
Сущность первого начала термодинамики заключается в следующем:
При сообщении термодинамической системе некоторого количества теплоты Q в общем случае происходит изменение внутренней энергии системы DU и система совершает работу А:
Является определением изменения внутренней энергии системы (DU), так как Q и А — независимо измеряемые величины.
Адиабатный процесс - процесс, происходящий в физической системе без теплообмена с окружающей средой. А. п. можно осуществить в системе, окруженной теплоизолирующей (адиабатной) оболочкой.
А. п. можно реализовать и при отсутствии адиабатной оболочки; для этого он должен протекать настолько быстро, чтобы за время процесса не произошло теплообмена между системой и окружающей средой. Адиабатное расширение газа с совершением работы против внешних сил и сил взаимного притяжения молекул вызывает его охлаждение. А. п. могут протекать обратимо и необратимо. В случае обратимого А. п. энтропия системы остаётся постоянной. Поэтому обратимый А. п. называют ещё изоэнтропийным.
 Адиабата - линия, изображающая на любой термодинамической диаграмме равновесный адиабатный процесс. Уравнение А. в этом случае: pug = const., где р — давление газа, u — его удельный объём, g — показатель адиабаты, постоянная для данного газа величина, равная отношению теплоёмкостей газа, определённых при постоянном давлении (cp) и постоянном объёме (cu); g = ср /cu.
Адиабата - линия, изображающая на любой термодинамической диаграмме равновесный адиабатный процесс. Уравнение А. в этом случае: pug = const., где р — давление газа, u — его удельный объём, g — показатель адиабаты, постоянная для данного газа величина, равная отношению теплоёмкостей газа, определённых при постоянном давлении (cp) и постоянном объёме (cu); g = ср /cu.
Политропный процесс - термодинамический процесс, характеризующийся постоянной теплоемкостью; для идеального газа описывается уравнением pVn=const, где n - постоянная, называемая показателем политропы.
Билет №11 Вопрос №1 Инерциальные системы отсчета. Преобразования Галилея. Принцип относительности Галилея.
Инерциальной называется такая система отсчета, в которой свободное движение тела с постоянной массой происходит с постоянной по величине и направлению скоростью.
Механический принцип относительности: Во всех инерциальных системах отсчета законы механики одинаковы + предложение об одинаковости течения времени во всех ИСО наз. принципом относительности Галилея.
Рассмотрим две ИСО, K(x, y, z, t) и K’(x’, y', z', t'), движущиеся друг относительно друга с постоянной скоростью 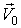 , вдоль направленияOX, рис.
, вдоль направленияOX, рис.
Предположим, что в начальный момент времени t обе координатные системы совпали, тогда
 . (1)
. (1)
Запишем (1) в проекциях
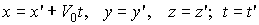 (2)
(2)
аналогичные соотношения между остальными координатами. Формулы обратного преобразования имеют вид
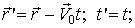 (3)
(3)
 . (4)
. (4)
Формулы (1) - (4) носят название преобразований Галилея. В них время считается абсолютным и поэтому не преобразуется.
Все физические величины, связанные со скоростью неинвариантны, а величины, связанные с ускорением, инвариантны по отношению к преобразованию Галилея.
Билет №11
Вопрос №2
Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы. Внутренняя энергия идеального газа. Классическая МКТ теплоемкости идеального газа. Связь числа степеней свободы с показателем адиабаты.
Важной характеристикой термодинамической системы является ее внутренняя энергия U - энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц. К внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.
Число степеней свободы i - это число независимых координат, полностью определяющих положение тела в пространстве. Для одноатомных молекул газа (He, Ne, Ar) i=3, для двухатомных молекул газа (H2, O2, N2) с жесткой связью атомов i=5, для трех- и более атомных молекул газа с жесткой связью атомов (CO2, NH3) i=6.
Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная kТ/2.
Следовательно, средняя кинетическая энергия молекулы, имеющей i степеней свободы, <Wk> = ikT/2.(1)
Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (т.е. молекулы между собой не взаимодействуют), то внутренняя энергия U представляет собой кинетическую энергию его молекул.
Для одного моля  ,(2)
,(2)
для произвольной массы m газа 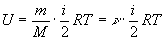 , где М - масса моля, n=m/M - число молей.
, где М - масса моля, n=m/M - число молей.
Таким образом, внутренняя энергия идеального газа пропорциональна температуре газа и зависит от числа степеней свободы его молекул.
Согласно классической молекулярно-кинетической теории теплоемкости
идеального газа
CV= iR/2
Cp= (i + 2)R/2
Показатель адиабаты 
Билет №12
Вопрос №1
Билет №12
Вопрос №2
Билет №11
Вопрос №2
Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы. Внутренняя энергия идеального газа. Классическая МКТ теплоемкости идеального газа. Связь числа степеней свободы с показателем адиабаты.
Важной характеристикой термодинамической системы является ее внутренняя энергия U - энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц. К внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.
Число степеней свободы i - это число независимых координат, полностью определяющих положение тела в пространстве. Для одноатомных молекул газа (He, Ne, Ar) i=3, для двухатомных молекул газа (H2, O2, N2) с жесткой связью атомов i=5, для трех- и более атомных молекул газа с жесткой связью атомов (CO2, NH3) i=6.
Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная kТ/2.
Следовательно, средняя кинетическая энергия молекулы, имеющей i степеней свободы, <Wk> = ikT/2.(1)
Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (т.е. молекулы между собой не взаимодействуют), то внутренняя энергия U представляет собой кинетическую энергию его молекул.
Для одного моля  ,(2)
,(2)
для произвольной массы m газа 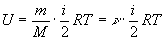 , где М - масса моля, n=m/M - число молей.
, где М - масса моля, n=m/M - число молей.
Таким образом, внутренняя энергия идеального газа пропорциональна температуре газа и зависит от числа степеней свободы его молекул.
Согласно классической молекулярно-кинетической теории теплоемкости
идеального газа
CV= iR/2
Cp= (i + 2)R/2
Показатель адиабаты 
Билет №12
Вопрос №1
Билет №12
Вопрос №2
Билет №13
Вопрос №1
Билет №13
Вопрос №2
Второе начало термодинамики является фундаментальным законом природы. Оно охватывает самый широкий круг природных явлений и указывает направление, в котором самопроизвольно протекают термодинамические процессы.
Второе начало термодинамики, как и первое, имеет несколько формулировок.
Невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, полностью в работу.
Эти формулировки показывают, что тепловые процессы являются необратимыми. Мерой необратимости процесса, мерой хаотичности является энтропия.
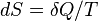
Возрастание энтропии системы при необратимом процессе выражает тот факт, что тепло само по себе не может переходить от менее нагретых к более нагретым телам. Последнее утверждение можно рассматривать также как формулировку второго начала термодинамики.
 , где константа k=1,38·10−23 Дж/К названа Планком постоянной Больцмана, а Omega — статистический вес состояния, является числом возможных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние.
, где константа k=1,38·10−23 Дж/К названа Планком постоянной Больцмана, а Omega — статистический вес состояния, является числом возможных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние.
Энтропией называется термодинамическая величина, изменение которой в системе пропорционально ее тепловой энергии, деленной на абсолютную температуру.
Знак неравенства ΔS > 0 относится к необратимым процессам. В реальных системах все процессы необратимы. Например, расширение газа, выравнивание температуры. Таким образом, второе начало термодинамики формулируется и как закон возрастания энтропии. Во всех необратимых процессах в замкнутой системе энтропия всегда возрастает.
Возрастание энтропии сопровождается выравниванием температуры или плотности газа. Это можно связать с порядком и беспорядком. Под порядком будем понимать сосредоточение частиц или энергии в определенном месте пространства, а под беспорядком (хаосом) - равномерное распределение их во всем объеме. Тогда возрастание энтропии при совершающихся без внешних воздействий необратимых процессах отражает природное стремление систем переходить от состояния более упорядоченного в состояние менее упорядоченное. Этот процесс сопровождается рассеянием энергии.
Билет №14
Вопрос №1
Вращательное движение твердого тела. Кинематические характеристики вращательного движения, угловое перемещение, угловая скорость, угловое ускорение и их связи с соответствующими линейными характеристиками.
Под вращательным движением абсолютно твердого тела понимают его движение как целого вокруг неподвижной оси, наз. осью вращения. При этом все точки твердого вращаются вокруг этой оси в параллел. плоскостях, описывая окружности с центрами лежащими на оси вращения. Все точки этого тела имеют разные по величине и направлению скорости.
Поэтому для описания вращ. движения вводятся угловые кинематические характеристики, единые для всего тела: угловое перемещение, угловая скорость и угловое ускорение.
Угловое перемещение есть акс. вектор равный отношению длины дуги, описываемой точкой, к радиусу вращения и направленный вдоль оси вращения по правилу винта:
 , гдеk – орт оси вращения.
, гдеk – орт оси вращения.
Угловой скоростью наз. предел, к которому стремиться отношение малого углового перемещения, определенного за некоторый интервал, к величине этого интервала при его стремление к нулю.
 Угловая скорость показывает быстроту изменения угла поворота.
Угловая скорость показывает быстроту изменения угла поворота.
Угловое ускорение: 
Угловая скорость и угловое ускорение также явл. акс. векторами.
Связь между линейной и угловой скоростью.
По рис.dl=Rdφ. Абсолютная величина угловой скорости определяется соотношением 
Поэтому  , а так как (dl/dt) есть линейная скорость точки, то
, а так как (dl/dt) есть линейная скорость точки, то 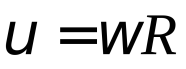
Связь между линейным и угловым ускорением. 
Билет №14
Вопрос №2
Билет №15
Вопрос №1
Динамика гармонических колебаний. Дифференциальное уравнение гармонических колебаний. Энергия гармонических колебаний. Примеры свободных колебательных систем: пружинный маятник, математический маятник, физический маятник.
Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Уравнение гармонических колебаний имеет вид x=ACos(wt+ф) или x=ASin(wt+ф) где x - смещение колеблющейся величины от положения равновесия.
Дифференциальное уравнение гармонических колебаний
Составим дифференциальное уравнение гармонических колебаний на примере пружинного маятника Сначала запишем уравнении динамики 2ой закон Ньютона: 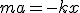
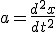 И теперь:
И теперь:  Делим на m и обозначаем
Делим на m и обозначаем  :
: 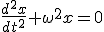 Это уравнение решается.
Это уравнение решается.
Энергия гармонических колебаний
По определению кинетическая энергия тела массой m, движущегося со скоростью  равна
равна 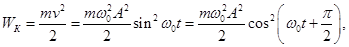


Потенциальная энергия равна 
Полная энергия равна 
Пружинный маятник - это груз массой m, закрепленный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы Fупр= - k x, где k - коэффициент упругости, в случае пружины называемый жесткостью. Уравнение движения маятника  или
или  . Из приведенных выражений следует, что пружинный маятник совершает гармонические колебания по закону х = A cos (w0 t + j), с циклической частотой
. Из приведенных выражений следует, что пружинный маятник совершает гармонические колебания по закону х = A cos (w0 t + j), с циклической частотой  и периодом
и периодом 
Математический маятник - материальная точка, совершающая под действием силы тяжести колебания вдоль дуги окружности, расположенной в вертикальной плоскости. Период  длина нити
длина нити
Физический маятник - абсолютно твердое тело, совершающее малые колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через его центр тяжести. 
Билет №15
Вопрос №2
Рапределение молекул по кинетическим энергиям ɛ их поступательного движения. График f(). Вычисления вероятнейшей ɛвер и средней <ɛ> кинетической энергии поступательного движения молекул.
Функция распределения по значениям кинетической энергии поступательного движения молекул, характеризующая вероятность попадания значений кинетической энергии в интервал:  . Приравняв вероятности
. Приравняв вероятности  или
или 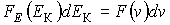 , и используя подстановку
, и используя подстановку  и
и  , имеем:
, имеем: 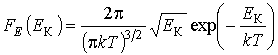 . Это распределение справедливо только для равновесного состояния термодинамической системы. Вследствие достаточно общего метода его получения, оно применимо не только для газов, но и для любых систем, движение микрочастиц которых описывается уравнениями классической механики.
. Это распределение справедливо только для равновесного состояния термодинамической системы. Вследствие достаточно общего метода его получения, оно применимо не только для газов, но и для любых систем, движение микрочастиц которых описывается уравнениями классической механики.
Вероятнейшее значение Определим производную функции 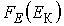 и приравняем её нулю:
и приравняем её нулю:  .Тогда имеем выражение для наиболее вероятного значения кинетической энергии :.
.Тогда имеем выражение для наиболее вероятного значения кинетической энергии :. 
Среднее значение: т.к. i=3, то <E>=3/2*k*T
Билет №16
Вопрос №1
Билет №16
Вопрос №2
Билет №17
Вопрос №1
Кинематика гармонических колебаний. Амплитуда, циклическая частота и фаза гармонических колебаний. Скорость и ускорение при гармонических колебаниях. Векторная диаграмма. Комплексное представление гармонических колебаний.
Гармоническими наз. колебания в любой физической системе, которые описываются величиной, изменяющейся по закону синуса или косинуса.
.
Амплитуда — модуль максимального отклонения тела от положения равновесия
Цикл. частота w - есть число колебаний осциллятора за 2π секунд: w = 2p/Т, Величина, обратная периоду колебаний Т, называется частотой ν = 1/Т = w/2p. Частота - есть число колебаний осциллятора за одну секунду.
Фаза колебания есть значение колеблющейся величины в данный момент времени.
Фаза гармонических колебаний Ф линейно растет со временем. При t = 0 значение Ф равняется j0, которое называется начальной фазой. Начальная фаза задает значение x в начальный момент времени. Начальную фазу и амплитуду гармонического осциллятора можно рассчитать исходя из начальных условий, подставив в уравнение колебательного движения и выражение для его скорости υ = dx/dt значение времени t = 0. Проделав соответствующие операции, получим:х(0) = х0 = А·cos(j0).u(0) = u0 = -А·w·sin(j0).где υ - скорость колеблющейся системы. Решив эту систему уравнений, получим, что величины амплитуды и начальной фазы опр. начальными условиями для рассматриваемой системы. A = (x02 + υ02/ω2)1/2; tg φ0 = -υ0/(x0·ω).
Найдем величины скорости и ускорения колебательного движения, описываемого уравнением: x = A·sin(w·t + j0). Поскольку ск-ть u - есть производная от координаты по времени, а ускорение - произв





 ,
, 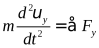 ,
, 
 ; V= iVх+jVу+kVz
; V= iVх+jVу+kVz a=iaх+jaу+kaz
a=iaх+jaу+kaz У скорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
У скорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. или
или  , где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно.
, где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно.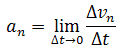


 ):
): 

 — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению
— вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению  . Чтобы найти её, необходимо вычислить
. Чтобы найти её, необходимо вычислить  , приравнять её нулю и решить относительно
, приравнять её нулю и решить относительно 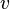 :
: 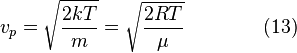



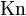 ) — один из критериев подобия движения разрежённых газов:
) — один из критериев подобия движения разрежённых газов:


 . Со стороны газа на поршень действуют сила, равная произведению давлению газа на поршень и площадь сечения поршня
. Со стороны газа на поршень действуют сила, равная произведению давлению газа на поршень и площадь сечения поршня  . Подставив вторую формулу в первую, получим
. Подставив вторую формулу в первую, получим  .
.
 , Дж/(кгК). (9)
, Дж/(кгК). (9)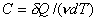 , Дж/(мольК). (10)где n=m/M - количество молей вещества.
, Дж/(мольК). (10)где n=m/M - количество молей вещества.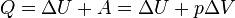
 )
) 


 ,
, 

 где
где 


 Адиабата - линия, изображающая на любой термодинамической диаграмме равновесный адиабатный процесс. Уравнение А. в этом случае: pug = const., где р — давление газа, u — его удельный объём, g — показатель адиабаты, постоянная для данного газа величина, равная отношению теплоёмкостей газа, определённых при постоянном давлении (cp) и постоянном объёме (cu); g = ср /cu.
Адиабата - линия, изображающая на любой термодинамической диаграмме равновесный адиабатный процесс. Уравнение А. в этом случае: pug = const., где р — давление газа, u — его удельный объём, g — показатель адиабаты, постоянная для данного газа величина, равная отношению теплоёмкостей газа, определённых при постоянном давлении (cp) и постоянном объёме (cu); g = ср /cu.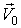 , вдоль направленияOX, рис.
, вдоль направленияOX, рис. . (1)
. (1)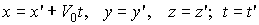 (2)
(2)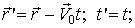 (3)
(3) . (4)
. (4) ,(2)
,(2)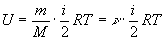 , где М - масса моля, n=m/M - число молей.
, где М - масса моля, n=m/M - число молей.
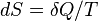
 , где константа k=1,38·10−23 Дж/К названа Планком постоянной Больцмана, а Omega — статистический вес состояния, является числом возможных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние.
, где константа k=1,38·10−23 Дж/К названа Планком постоянной Больцмана, а Omega — статистический вес состояния, является числом возможных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние. , гдеk – орт оси вращения.
, гдеk – орт оси вращения. Угловая скорость показывает быстроту изменения угла поворота.
Угловая скорость показывает быстроту изменения угла поворота.

 , а так как (dl/dt) есть линейная скорость точки, то
, а так как (dl/dt) есть линейная скорость точки, то 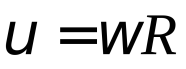

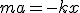
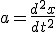 И теперь:
И теперь:  Делим на m и обозначаем
Делим на m и обозначаем  :
: 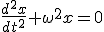 Это уравнение решается.
Это уравнение решается. равна
равна 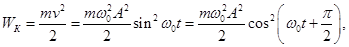




 или
или  . Из приведенных выражений следует, что пружинный маятник совершает гармонические колебания по закону х = A cos (w0 t + j), с циклической частотой
. Из приведенных выражений следует, что пружинный маятник совершает гармонические колебания по закону х = A cos (w0 t + j), с циклической частотой  и периодом
и периодом 
 длина нити
длина нити
 . Приравняв вероятности
. Приравняв вероятности  или
или 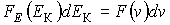 , и используя подстановку
, и используя подстановку  и
и  , имеем:
, имеем: 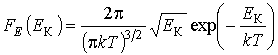 . Это распределение справедливо только для равновесного состояния термодинамической системы. Вследствие достаточно общего метода его получения, оно применимо не только для газов, но и для любых систем, движение микрочастиц которых описывается уравнениями классической механики.
. Это распределение справедливо только для равновесного состояния термодинамической системы. Вследствие достаточно общего метода его получения, оно применимо не только для газов, но и для любых систем, движение микрочастиц которых описывается уравнениями классической механики.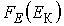 и приравняем её нулю:
и приравняем её нулю:  .Тогда имеем выражение для наиболее вероятного значения кинетической энергии :.
.Тогда имеем выражение для наиболее вероятного значения кинетической энергии :. 


