Представление и обработка данных в виде графов

Графы формально описывают множество близких ситуаций. Самым привычным примером служит карта автодорог, на которой изображены перекрестки и связыва­ющие их дороги. Перекрестки являются вершинами графа, а дороги — его ребрами. Графы могут быть ориентированы (подобно улицам с односторонним движением) или взвешены, когда каждой дороге приписана стоимость путешествия по ней (если, например, дороги платные).

С формальной точки зрения граф представляет собой упорядоченную пару мно­жеств G = (V, Е), первое из которых состоит из вершин (узлов) графа, а второе — из его ребер. Ребро связывает между собой две вершины. При работе с графами часто решается вопрос, как проложить путь из ребер от одной вершины графа к другой. В этом случае говорят о движении по ребру, что означает переход из вершины А гра­фа в другую вершину 5, связанную с ней ребром АВ (ребро графа, связывающее две вершины, для краткости обозначается этой парой вершин). В этом случае говорят, что ребро А примыкает к ребру В или что эти две вершины соседние.

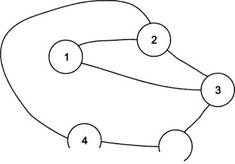
Граф может быть ориентированным или нет. Ребра неориентированного гра­фа, чаще всего называемого просто графом, можно проходить в обоих направле­ниях (рис. 14.26). В этом случае ребро — это неупорядоченная пара вершин, его концов.

5

Граф G = ({1, 2, 3, 4, 5 }, {{1, 2}, {1, 3 }, Рис. 14.26. Неориентированный граф

В ориентированном графе, или орграфе, ребра представляют собой упорядочен­ные пары вершин: первая вершина — это начало ребра, вторая — его конец (рис. 14.27).

Полный граф — это граф, в котором каждая вершина соединена со всеми осталь­ными. Количество ребер в полном графе без петель с N вершинами равно (Л/² -ЛГ)/2. В полном ориентированном графе разрешается переход из любой вершины в любую другую. Поскольку в графе переход по ребру разрешается в обоих направ-

14.4. Представление и обработка данных разного типа 421

лениях, а переход по ребру в орграфе — только в одном, в полном орграфе в два раза больше ребер, то есть их количество равно N² - N.

4 *—'

Ориентированный

Рис. 14.27. Ориентированный граф

Подграф (V_S,E_S) графа или орграфа (V_yE) состоит из некоторого подмножества вершин, V_s С V, и некоторого подмножества ребер, их соединяющих, E_s С Е.

Путь в графе или орграфе — это последовательность ребер, по которым можно поочередно проходить. Другими словами, путь из вершины А в вершину В начина­ется в Л и проходит по набору ребер до тех пор, пока не будет достигнута вершина В. С формальной точки зрения путь из вершины V_x в вершину V_y — это последова­тельность ребер графа:

Необходимо, чтобы любая вершина встречалась на таком пути не более, чем однажды. У всякого пути есть длина — количество ребер в нем. Длина пути АВ, ВС, СДДЕ равна 4.

Граф или орграф называется связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл — это путь, который начинается и кончается в одной и той же вершине. В ациклическом графе или орграфе циклы отсутствуют. Связный ациклический граф называется неукорененным деревом. Структура неуко-рененного дерева такая же, как и у дерева, только в нем не выделен корень. Однако каждая вершина неукорененного дерева может служить его корнем.

Информацию о графах или орграфах в пригодном для обработки компьютер­ными алгоритмами виде можно хранить двумя способами: в виде матрицы при­мыканий и в виде списка примыканий^.

Матрица примыканий обеспечивает быстрый доступ к информации о ребрах графа, однако, если в графе мало ребер, эта матрица будет содержать гораздо боль­ше пустых клеток, чем заполненных. Длина списка примыканий пропорциональна числу ребер в графе, однако при пользовании списком время получения информа­ции о ребре увеличивается.

¹ В определенных конкретных случаях может потребоваться представления и в других формах, также пригодных к обработке на компьютере: в виде матриц инцидентности или матриц смежно­сти, а также других структур для представления «веса» и «цвета» связей, пометок вершин и т. д.