С изменением приложенных к системе нагрузок и длины трещины изменяется икоэффициент интенсивности напряжений. Очевидно, предельному состоянию конструкции будет соответствовать достижение КИНом некоторой критическойвеличины, зависящей от геометрических параметров объекта и свойств материала. Таким образом, возникает проблема получения спе  цифической прочностной характеристики материала, определяющей его сопротивление хрупкому разрушению – так называемой вязкости разрушенияK Ic(критического значения КИН) (не путать с ударной вязкостью). Как уже было сказано, индексом «с» отмечаются критические (соответствующие моменту страгивания трещины) значения того или иного параметра.
цифической прочностной характеристики материала, определяющей его сопротивление хрупкому разрушению – так называемой вязкости разрушенияK Ic(критического значения КИН) (не путать с ударной вязкостью). Как уже было сказано, индексом «с» отмечаются критические (соответствующие моменту страгивания трещины) значения того или иного параметра.
 К настоящему времени разработаны и введены в действие национальные и отраслевые нормативные документы, регламентирующие порядок экспериментального определения характеристик трещиностойкости материала, например, межгосударственный стандарт ГОСТ 25.506–85 «Расчеты и испытания на прочность. Методы механических испытаний металлов. Определение характеристик трещиностойкости (вязкости разрушения) при статическом нагружении»[4], стандарт ASTM (AmericanSocietyforTestingandMaterials– американскоймеждународной добровольной организации, разрабатывающей и издающей стандартыдля материалов, продуктов, систем и услуг), британский национальный стандарт и др. Эти документы устанавливают типы образцов, условия их изготовления и подготовки к испытаниям, требования к условиям испытаний, оборудованию и регистрирующей аппаратуре, а также определяют порядок обработки экспериментальных данных и устанавливают критерии корректности получаемых результатов. В частности, механическая часть испытательной установки должна обладать высокой жесткостью и способностью развивать высокие усилия. Регистрирующая аппаратура должна обеспечивать фиксацию усилий и небольших по величине перемещений, изменяющихся с высокой скоростью. На рис. 4.20показаны испытательные машины, представляющие крайние по развиваемому усилию позиции в линейке производственной программы фирмы MTSSystems (США).
К настоящему времени разработаны и введены в действие национальные и отраслевые нормативные документы, регламентирующие порядок экспериментального определения характеристик трещиностойкости материала, например, межгосударственный стандарт ГОСТ 25.506–85 «Расчеты и испытания на прочность. Методы механических испытаний металлов. Определение характеристик трещиностойкости (вязкости разрушения) при статическом нагружении»[4], стандарт ASTM (AmericanSocietyforTestingandMaterials– американскоймеждународной добровольной организации, разрабатывающей и издающей стандартыдля материалов, продуктов, систем и услуг), британский национальный стандарт и др. Эти документы устанавливают типы образцов, условия их изготовления и подготовки к испытаниям, требования к условиям испытаний, оборудованию и регистрирующей аппаратуре, а также определяют порядок обработки экспериментальных данных и устанавливают критерии корректности получаемых результатов. В частности, механическая часть испытательной установки должна обладать высокой жесткостью и способностью развивать высокие усилия. Регистрирующая аппаратура должна обеспечивать фиксацию усилий и небольших по величине перемещений, изменяющихся с высокой скоростью. На рис. 4.20показаны испытательные машины, представляющие крайние по развиваемому усилию позиции в линейке производственной программы фирмы MTSSystems (США).
Российским ГОСТ 25.506–85 предусматривается использование образцов нескольких типов, некоторые из них представлены на рис. 4.21. Ниже приведены выражения для коэффициента интенсивности напряженийдвух наиболее распространенных в практике экспериментальных исследований образцов – компактного
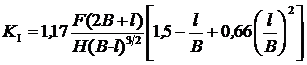 или
или

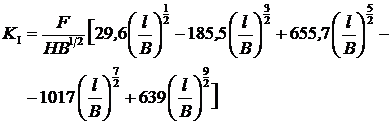
и в виде балки для испытания в условиях трехточечного изгиба
 или
или
 ,
,

а также цилиндрический образец с круговым надрезом.
После изготовления образцов, перед тем, как приступить к испытаниям, в вершине стартовой выточки шевронной формы (рис. 4.21) выращивают усталостную трещину, причем во избежание «притупления» ее кончика (образования зоны пластичности недопустимой величины) ограничивается максимальное в цикле значение КИН
K Imax£ 0,6 K Ic.


Определенные ограничения накладываются также на длину начальной трещины и на форму ее фронта.

В результате обработки данных испытаний на вязкость разрушения было обнаружено, что предельные (критические) значения K I Q коэффициента интенсивности напряжений изменяются доопределенного предела в зависимости от толщины образца (рис. 4.22).Посколькув диапазоне толщин 0< H £ H 1 геометрические параметры системы оказывают влияние на трещиностойкость объекта, логично предположить, что в этом случае онахарактеризует не только свойства материала. Для прояснения этогообстоятельства рассмотрим структуру потребных для разрушения энергозатрат в системе «образец – нагружающее устройство»(рис. 4.23).Как правило, бóльшая часть работы, совершаемойпри перемещении захватов испытательной машины, расходуется на изменение потенциальной энергии упругого деформирования образца, расчет которой в упругой  постановке не представляет принципиальных трудностей.Определенная часть поступившей в систему энергиирассеивается в пространстве в виде тепла в результате работы, совершаемой напряжениями на пластических деформациях. Корректное определение диссипации энергии представляет гораздо более сложную задачу, поскольку требует расчета полей напряжений и деформаций в области вершины трещины с учетом реальной диаграммы деформированияматериала. В свою очередь, размер зоны пластичности зависит от пластических свойств материала и вида напряженного состояния (минимальному,как видно на рис. 4.16, отвечает плоское деформированное состояние, напряженное состояние при этом является объемным). Поскольку полностью от зоны неупругого деформирования в сталях и сплавах–материалах пластичных – избавиться не удается, а выделить диссипацию при обработке результатов испытания трудно, ее можно учесть, условно включив в затраты энергии, пошедшей непосредственно на разрушение, тем более, что доля последней относительно невелика.
постановке не представляет принципиальных трудностей.Определенная часть поступившей в систему энергиирассеивается в пространстве в виде тепла в результате работы, совершаемой напряжениями на пластических деформациях. Корректное определение диссипации энергии представляет гораздо более сложную задачу, поскольку требует расчета полей напряжений и деформаций в области вершины трещины с учетом реальной диаграммы деформированияматериала. В свою очередь, размер зоны пластичности зависит от пластических свойств материала и вида напряженного состояния (минимальному,как видно на рис. 4.16, отвечает плоское деформированное состояние, напряженное состояние при этом является объемным). Поскольку полностью от зоны неупругого деформирования в сталях и сплавах–материалах пластичных – избавиться не удается, а выделить диссипацию при обработке результатов испытания трудно, ее можно учесть, условно включив в затраты энергии, пошедшей непосредственно на разрушение, тем более, что доля последней относительно невелика.
Итак, основным требованием, предъявляемым к образцам, является обеспечение плоского деформированного состояния в вершине трещиныс тем, чтобы до минимума сократить диссипацию энергии при неупругом деформировании материала внутри зоны пластичности и, таким образом, повысить долю энергии, затрачиваемой непосредственно на разруше  ние связей в материале (образование новых поверхностей) в общих энергетических затратах. Только в этом случае можно утверждать, что полученная величина является характеристикой трещиностойкости именно материала, а не образца из этого материала.
ние связей в материале (образование новых поверхностей) в общих энергетических затратах. Только в этом случае можно утверждать, что полученная величина является характеристикой трещиностойкости именно материала, а не образца из этого материала.
Указанное требование обеспечивается выполнением соотношения r Т<< Н. Так как размер зоны пластичности r Тпропорционален отношению  – см. выражение (4.2) – то в условиях ПДС при разрушении должно выполняться неравенство
– см. выражение (4.2) – то в условиях ПДС при разрушении должно выполняться неравенство 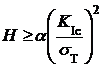 . Границе
. Границе  для разных материалов соответствуют разные значения a:
для разных материалов соответствуют разные значения a:

последняявеличина принята в стандарте ASTM в качестве критерияправиль
ного выбора размеров образца (рис. 4.22).
Одним из условий правомерности применения подходов линейной механики разрушения (ЛМР) является также выполнение соотношения l >> r Т.Это означает, чтотрещина должна быть,как говорят, «длинной», то есть, ее длина должна быть намного больше размера зоны пластической деформации в вершине трещиныЗависимостьпредельногокоэффициента интенсивности напряжений K I Q от отношения  имеет характер, аналогичныйобсуждавшемуся выше
имеет характер, аналогичныйобсуждавшемуся выше  . Таким образом, условия существования ПДС в процессе испытаний и правомерности применения математического аппарата ЛМР могут быть записаны в виде
. Таким образом, условия существования ПДС в процессе испытаний и правомерности применения математического аппарата ЛМР могут быть записаны в виде
 ;
;
 .
.
По приводимым в литературе оценкам закономерности ЛМР справедливы, если номинальное напряжениеневелико: s £0,66 s 0,2.
Учитывая, что критический (в момент разрушения) размер зоны пластич  ности в соответствии с уточненной оценкой (см. (4.3)) в условиях ПДС равен
ности в соответствии с уточненной оценкой (см. (4.3)) в условиях ПДС равен
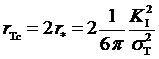 ,
,
величины Н и l должны быть, по крайней мере, в 25 раз больше значения параметра r Т. Поэтому для высокопластичных материалов, обладающих небольшим пределом текучестии значительной вязкостью разрушения, размеры, в том числе, толщина образца, могут оказаться весьма внушительными, что, в свою очередь, потребует испытательных установок с высоким разрывным усилием.
Заметим, что важнейшее условие корректности испытаний (реализация ПДС) по-видимому не будет выполняться в большинстве случаев при испытании плоских образцов (рис. 4.21),поэтому соответствующие результаты можно рассматривать лишь как сравнительные или в качестве технологической пробы.
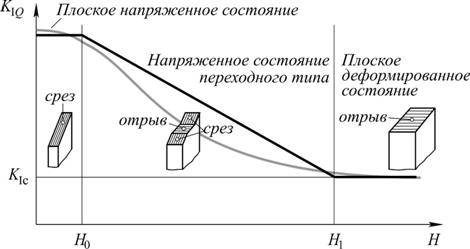 В тех случаях, когда анализ трещиностойкости носит приближенный или качественный характер, экспериментальную зависимость K I Q (Н) допустимоаппроксимировать предложенной Андерсоном кусочно-линейной функцией (рис. 4.24, там же показан преимущественный характер разрушения образцов в зонах, отвечающих разному типу напряженно-деформированного состояния). Как видно, размер Н 1 отвечает объекту, в котором реализуется ПДС:
В тех случаях, когда анализ трещиностойкости носит приближенный или качественный характер, экспериментальную зависимость K I Q (Н) допустимоаппроксимировать предложенной Андерсоном кусочно-линейной функцией (рис. 4.24, там же показан преимущественный характер разрушения образцов в зонах, отвечающих разному типу напряженно-деформированного состояния). Как видно, размер Н 1 отвечает объекту, в котором реализуется ПДС:

 (4.4)
(4.4)
(в соответствии с рекомендациями ASTMпринято a =2,5).Максимальная толщина Н 0,при которой еще может реализоваться ПНС, имеет тот же порядок,что и зона пластичности при ПДС:
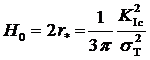 . .
| (4.5)
|



 Определение скорости трещиныв ходе испытаний производили с помощью сетки токопроводящих полос, последовательно разрываемых бегущей трещиной (рис. 4.25);таким способомудается связать приращение ее длины(D l –шаг сетки) со временем. В результате былоустановлено, что скорость
Определение скорости трещиныв ходе испытаний производили с помощью сетки токопроводящих полос, последовательно разрываемых бегущей трещиной (рис. 4.25);таким способомудается связать приращение ее длины(D l –шаг сетки) со временем. В результате былоустановлено, что скорость 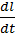 изменяется немонотонно:трещина периодически то разгоняется, то тормозится, а на диаграмме «усилие~раскрытие трещины» зачастую присутствуют практически горизонтальные плато (рис. 4.26).
изменяется немонотонно:трещина периодически то разгоняется, то тормозится, а на диаграмме «усилие~раскрытие трещины» зачастую присутствуют практически горизонтальные плато (рис. 4.26).

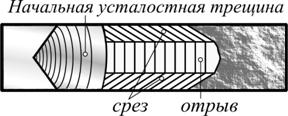
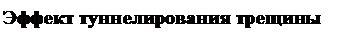 Эту особенность объясняют эффектом «туннелирования трещины»(рис. 4.27), который наблюдается при реализации в испытуемом объекте плоского деформированного или напряженного состояния переходного типа: вначале фронт трещины заскакивает вперед, пробивая своеобразный туннель в срединной области тела, где трещиностойкость материала в силу стеснения пластического течения ниже. При этом нарушается баланс между подводимой и поглощаемой энергией, трещина тормозится в ожидании подтягивающихся флангов, где разрушение происходит медленнее, преимущественно путем среза.Далее процесс повторяется.
Эту особенность объясняют эффектом «туннелирования трещины»(рис. 4.27), который наблюдается при реализации в испытуемом объекте плоского деформированного или напряженного состояния переходного типа: вначале фронт трещины заскакивает вперед, пробивая своеобразный туннель в срединной области тела, где трещиностойкость материала в силу стеснения пластического течения ниже. При этом нарушается баланс между подводимой и поглощаемой энергией, трещина тормозится в ожидании подтягивающихся флангов, где разрушение происходит медленнее, преимущественно путем среза.Далее процесс повторяется.
Как следует из рис. 4.22, 4.24, в условиях, отличных от ПДС, критическое  значение коэффициента интенсивности напряжений K I Q оказывается выше вязкости разрушения материала, что открывает определенные резервы прочности.По аналогии с критерием Е.М. Морозова (см. ниже) будем называть его пределом трещиностойкости и обозначать в дальнейшем K 1с(индекс «1» по-прежнему соответствует трещине нормального отрыва). Его величину в зависимости от вязкости разрушения K Iс, характеристик прочности и пластичности, а также толщины Н рассматриваемого элемента конструкции можно оценить с помощью довольно простой формуле, предложенной Броеком и Влигером,
значение коэффициента интенсивности напряжений K I Q оказывается выше вязкости разрушения материала, что открывает определенные резервы прочности.По аналогии с критерием Е.М. Морозова (см. ниже) будем называть его пределом трещиностойкости и обозначать в дальнейшем K 1с(индекс «1» по-прежнему соответствует трещине нормального отрыва). Его величину в зависимости от вязкости разрушения K Iс, характеристик прочности и пластичности, а также толщины Н рассматриваемого элемента конструкции можно оценить с помощью довольно простой формуле, предложенной Броеком и Влигером,
 . .
| (4.6)
|

 где
где 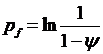 как и прежде, ресурс пластичности материала.
как и прежде, ресурс пластичности материала.
С повышением нагрузки на образец все более заметной становится нелинейная составляющая взаимного смещения берегов трещины (рис. 4.28). Поскольку до нагрузки определенной величины длина трещины остается неизменной, нелинейность кривой F ~ 2 v (v – полураскрытие трещины) полностью определяется пластическим деформированием материала в ее вершине.
 Далее следует этап стабильного(контролируемого) роста трещины (это означает, что определенной нагрузкесоответствует фиксированный текущий размер трещины, иными словами, на этом этапе ее рост можно приостановить). Нелинейность упомянутой диаграммы определяется разного родаснижающими жесткость системы факторами – физического (пластическое деформирование) и геометрического (подрастание трещины) характера.
Далее следует этап стабильного(контролируемого) роста трещины (это означает, что определенной нагрузкесоответствует фиксированный текущий размер трещины, иными словами, на этом этапе ее рост можно приостановить). Нелинейность упомянутой диаграммы определяется разного родаснижающими жесткость системы факторами – физического (пластическое деформирование) и геометрического (подрастание трещины) характера.
 По мере роста усилия скорость трещины увеличивается нарастающим темпом, ее стабильное развитие сменяется нестабильным, лавинообразным;в итоге происходит разделение образца на части.Конечно, четкую границу между этими двумя этапами провести невозможно, поэтому в качестве расчетной разрушающей нагрузки FQ принимается такая, при которой нелинейная составляющая x 2раскрытия трещиныза счет ее продвижения и пластической деформации не превышает 5 % «упругого» раскрытия
По мере роста усилия скорость трещины увеличивается нарастающим темпом, ее стабильное развитие сменяется нестабильным, лавинообразным;в итоге происходит разделение образца на части.Конечно, четкую границу между этими двумя этапами провести невозможно, поэтому в качестве расчетной разрушающей нагрузки FQ принимается такая, при которой нелинейная составляющая x 2раскрытия трещиныза счет ее продвижения и пластической деформации не превышает 5 % «упругого» раскрытия  при той же нагрузке. На рис. 4.28 показана схема определения усилия FQ: точка пересечения луча I, проведенного из начала координат под углом a 1, таким, что tg a 1 = 0,95 tg a, с экспериментальной кривой определяет величину расчетной разрушающей нагрузки FQ. Обратите внимание, что данное условие касается тангенса угла a 1, а не самого угла. Как видно, вспомогательный луч II с углом наклона a следует линейному участку диаграммы и отвечает как геометрически, так и физически линейному поведению объекта.
при той же нагрузке. На рис. 4.28 показана схема определения усилия FQ: точка пересечения луча I, проведенного из начала координат под углом a 1, таким, что tg a 1 = 0,95 tg a, с экспериментальной кривой определяет величину расчетной разрушающей нагрузки FQ. Обратите внимание, что данное условие касается тангенса угла a 1, а не самого угла. Как видно, вспомогательный луч II с углом наклона a следует линейному участку диаграммы и отвечает как геометрически, так и физически линейному поведению объекта.
Кроме того, для корректного определения критической длины lc трещины необходимо, чтобы она как можно дольше оставалась неподвижной. В качестве компромисса обычно принимаютвеличину 0,8 FQ, определяющую нижнюю границу этапа контролируемого роста трещины. В этом случае нелинейные составляющие раскрытия должны отвечать условию

Показанная на рис. 4.28зависимость F ~ v типичнадля подавляющего большинства сталей и сплавов, однако в практике экспериментальных исследований встречаются и диаграммы иного вида. Соответствующие схемы определения расчетного разрушающего усилия FQ показаны на рис. 4.29.
Подводя итог сказанному, представим порядок экспериментального определения вязкости разрушения K Iсматериала в виде блок-схемы (рис.4.30).
В табл. 4.1 приведены значения вязкости разрушения некоторых материалов, значительно различающихся своими механическими свойствами; для сравненияв таблицу включена также характеристика трещиностойкости стеклакак классического хрупкого материала.

 Таблица 4.1
Таблица 4.1
Вязкость разрушения некоторых материалов
| Материал
| Предел текучести s 0,2, МПа
| Пределпрочности s В, МПа
| Вязкость разрушения K Iс
|
| МН/м3/2
| кГ/мм3/2
|
| Малоугл.сталь Ст.3
|
| 380…470
| 24,8
|
|
| Легир. сталь 40ХН
|
|
| 70,1
|
|
| Титан. сплав ВТ14
| 900…1100
| 1080…1300
| 52,7
|
|
| Силикатное стекло
| –
| –
| 0,53
| 1,7
|
Примечание:

Обратите внимание на отсутствие строгой корреляции между традиционными характеристиками прочности и вязкостью разрушения. Попытка прогнозирования последней по пределу текучести или пределупрочности может привести к ошибке качественного характера.
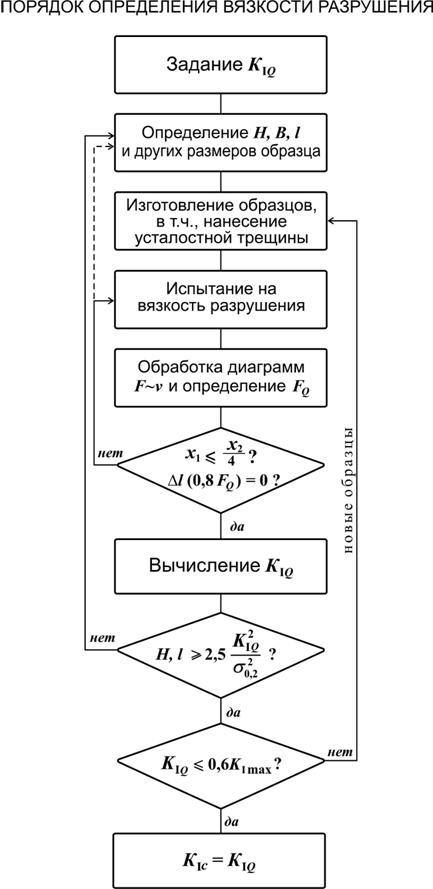
 Рис. 4.30 Порядок экспериментального определения вязкости разрушения
Рис. 4.30 Порядок экспериментального определения вязкости разрушения
 Пример 4.1. В результате испытания на вязкость разрушения компактного
Пример 4.1. В результате испытания на вязкость разрушения компактного  образца, о котором известно следующее: H =25 мм, В = 20 мм, lc = 10 мм, предел текучести стали s 0,2 =380 МПа,получена кривая«усилие~полураскрытие трещины» и найдена расчетная разрушающая нагрузка FQ =13,2кН.
образца, о котором известно следующее: H =25 мм, В = 20 мм, lc = 10 мм, предел текучести стали s 0,2 =380 МПа,получена кривая«усилие~полураскрытие трещины» и найдена расчетная разрушающая нагрузка FQ =13,2кН.
Необходимо определить величину и тип характеристикитрещиностойкости.
Решение. Подставляя в формулу для коэффициента интенсивности напряжений компактного образца (см.выражение в начале данного подраздела) известные размеры и значение нагрузки FQ с учетом  ,вычислим критическое значение КИН
,вычислим критическое значение КИН

Затем подсчитаем величину  и сравним с ней толщину образца Н: 25 > 22,3 мм – в образце обеспечено плоское деформированное состояние – и критическую длину трещины lc: 10 < 22,3 мм – трещина оказалась недостаточно «длинной», т.е., размер зоны пластичности слишком велик по сравнению с длиной трещины, а, значит, все использованные соотношения ЛМР неприменимы.
и сравним с ней толщину образца Н: 25 > 22,3 мм – в образце обеспечено плоское деформированное состояние – и критическую длину трещины lc: 10 < 22,3 мм – трещина оказалась недостаточно «длинной», т.е., размер зоны пластичности слишком велик по сравнению с длиной трещины, а, значит, все использованные соотношения ЛМР неприменимы.
Таким образом, рассматриваемое испытание оказалось некорректным, а найденная величина K I Q = 35,58  представляет собой предел трещиностойкости ихарактеризует лишь трещиностойкость образца из данной стали.
представляет собой предел трещиностойкости ихарактеризует лишь трещиностойкость образца из данной стали.
Из всего сказанного следует:отличительная особенность силового подхода к оценке трещиностойкости элементов конструкций состоитв сопоставлении текущего значения коэффициента интенсивности напряжений с его критическим (предельным) значением.
 4.8Применение силового подходак оценке
4.8Применение силового подходак оценке





 цифической прочностной характеристики материала, определяющей его сопротивление хрупкому разрушению – так называемой вязкости разрушенияK Ic(критического значения КИН) (не путать с ударной вязкостью). Как уже было сказано, индексом «с» отмечаются критические (соответствующие моменту страгивания трещины) значения того или иного параметра.
цифической прочностной характеристики материала, определяющей его сопротивление хрупкому разрушению – так называемой вязкости разрушенияK Ic(критического значения КИН) (не путать с ударной вязкостью). Как уже было сказано, индексом «с» отмечаются критические (соответствующие моменту страгивания трещины) значения того или иного параметра. К настоящему времени разработаны и введены в действие национальные и отраслевые нормативные документы, регламентирующие порядок экспериментального определения характеристик трещиностойкости материала, например, межгосударственный стандарт ГОСТ 25.506–85 «Расчеты и испытания на прочность. Методы механических испытаний металлов. Определение характеристик трещиностойкости (вязкости разрушения) при статическом нагружении»[4], стандарт ASTM (AmericanSocietyforTestingandMaterials– американскоймеждународной добровольной организации, разрабатывающей и издающей стандартыдля материалов, продуктов, систем и услуг), британский национальный стандарт и др. Эти документы устанавливают типы образцов, условия их изготовления и подготовки к испытаниям, требования к условиям испытаний, оборудованию и регистрирующей аппаратуре, а также определяют порядок обработки экспериментальных данных и устанавливают критерии корректности получаемых результатов. В частности, механическая часть испытательной установки должна обладать высокой жесткостью и способностью развивать высокие усилия. Регистрирующая аппаратура должна обеспечивать фиксацию усилий и небольших по величине перемещений, изменяющихся с высокой скоростью. На рис. 4.20показаны испытательные машины, представляющие крайние по развиваемому усилию позиции в линейке производственной программы фирмы MTSSystems (США).
К настоящему времени разработаны и введены в действие национальные и отраслевые нормативные документы, регламентирующие порядок экспериментального определения характеристик трещиностойкости материала, например, межгосударственный стандарт ГОСТ 25.506–85 «Расчеты и испытания на прочность. Методы механических испытаний металлов. Определение характеристик трещиностойкости (вязкости разрушения) при статическом нагружении»[4], стандарт ASTM (AmericanSocietyforTestingandMaterials– американскоймеждународной добровольной организации, разрабатывающей и издающей стандартыдля материалов, продуктов, систем и услуг), британский национальный стандарт и др. Эти документы устанавливают типы образцов, условия их изготовления и подготовки к испытаниям, требования к условиям испытаний, оборудованию и регистрирующей аппаратуре, а также определяют порядок обработки экспериментальных данных и устанавливают критерии корректности получаемых результатов. В частности, механическая часть испытательной установки должна обладать высокой жесткостью и способностью развивать высокие усилия. Регистрирующая аппаратура должна обеспечивать фиксацию усилий и небольших по величине перемещений, изменяющихся с высокой скоростью. На рис. 4.20показаны испытательные машины, представляющие крайние по развиваемому усилию позиции в линейке производственной программы фирмы MTSSystems (США).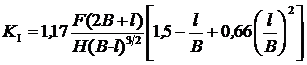 или
или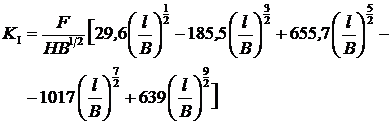
 или
или ,
,




 постановке не представляет принципиальных трудностей.Определенная часть поступившей в систему энергиирассеивается в пространстве в виде тепла в результате работы, совершаемой напряжениями на пластических деформациях. Корректное определение диссипации энергии представляет гораздо более сложную задачу, поскольку требует расчета полей напряжений и деформаций в области вершины трещины с учетом реальной диаграммы деформированияматериала. В свою очередь, размер зоны пластичности зависит от пластических свойств материала и вида напряженного состояния (минимальному,как видно на рис. 4.16, отвечает плоское деформированное состояние, напряженное состояние при этом является объемным). Поскольку полностью от зоны неупругого деформирования в сталях и сплавах–материалах пластичных – избавиться не удается, а выделить диссипацию при обработке результатов испытания трудно, ее можно учесть, условно включив в затраты энергии, пошедшей непосредственно на разрушение, тем более, что доля последней относительно невелика.
постановке не представляет принципиальных трудностей.Определенная часть поступившей в систему энергиирассеивается в пространстве в виде тепла в результате работы, совершаемой напряжениями на пластических деформациях. Корректное определение диссипации энергии представляет гораздо более сложную задачу, поскольку требует расчета полей напряжений и деформаций в области вершины трещины с учетом реальной диаграммы деформированияматериала. В свою очередь, размер зоны пластичности зависит от пластических свойств материала и вида напряженного состояния (минимальному,как видно на рис. 4.16, отвечает плоское деформированное состояние, напряженное состояние при этом является объемным). Поскольку полностью от зоны неупругого деформирования в сталях и сплавах–материалах пластичных – избавиться не удается, а выделить диссипацию при обработке результатов испытания трудно, ее можно учесть, условно включив в затраты энергии, пошедшей непосредственно на разрушение, тем более, что доля последней относительно невелика. – см. выражение (4.2) – то в условиях ПДС при разрушении должно выполняться неравенство
– см. выражение (4.2) – то в условиях ПДС при разрушении должно выполняться неравенство 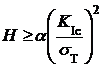 . Границе
. Границе  для разных материалов соответствуют разные значения a:
для разных материалов соответствуют разные значения a:
 имеет характер, аналогичныйобсуждавшемуся выше
имеет характер, аналогичныйобсуждавшемуся выше  . Таким образом, условия существования ПДС в процессе испытаний и правомерности применения математического аппарата ЛМР могут быть записаны в виде
. Таким образом, условия существования ПДС в процессе испытаний и правомерности применения математического аппарата ЛМР могут быть записаны в виде ;
; .
.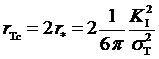 ,
, В тех случаях, когда анализ трещиностойкости носит приближенный или качественный характер, экспериментальную зависимость K I Q (Н) допустимоаппроксимировать предложенной Андерсоном кусочно-линейной функцией (рис. 4.24, там же показан преимущественный характер разрушения образцов в зонах, отвечающих разному типу напряженно-деформированного состояния). Как видно, размер Н 1 отвечает объекту, в котором реализуется ПДС:
В тех случаях, когда анализ трещиностойкости носит приближенный или качественный характер, экспериментальную зависимость K I Q (Н) допустимоаппроксимировать предложенной Андерсоном кусочно-линейной функцией (рис. 4.24, там же показан преимущественный характер разрушения образцов в зонах, отвечающих разному типу напряженно-деформированного состояния). Как видно, размер Н 1 отвечает объекту, в котором реализуется ПДС:
 (4.4)
(4.4)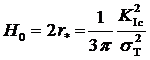 .
.



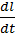 изменяется немонотонно:трещина периодически то разгоняется, то тормозится, а на диаграмме «усилие~раскрытие трещины» зачастую присутствуют практически горизонтальные плато (рис. 4.26).
изменяется немонотонно:трещина периодически то разгоняется, то тормозится, а на диаграмме «усилие~раскрытие трещины» зачастую присутствуют практически горизонтальные плато (рис. 4.26).

 Эту особенность объясняют эффектом «туннелирования трещины»(рис. 4.27), который наблюдается при реализации в испытуемом объекте плоского деформированного или напряженного состояния переходного типа: вначале фронт трещины заскакивает вперед, пробивая своеобразный туннель в срединной области тела, где трещиностойкость материала в силу стеснения пластического течения ниже. При этом нарушается баланс между подводимой и поглощаемой энергией, трещина тормозится в ожидании подтягивающихся флангов, где разрушение происходит медленнее, преимущественно путем среза.Далее процесс повторяется.
Эту особенность объясняют эффектом «туннелирования трещины»(рис. 4.27), который наблюдается при реализации в испытуемом объекте плоского деформированного или напряженного состояния переходного типа: вначале фронт трещины заскакивает вперед, пробивая своеобразный туннель в срединной области тела, где трещиностойкость материала в силу стеснения пластического течения ниже. При этом нарушается баланс между подводимой и поглощаемой энергией, трещина тормозится в ожидании подтягивающихся флангов, где разрушение происходит медленнее, преимущественно путем среза.Далее процесс повторяется. .
.

 где
где 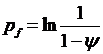 как и прежде, ресурс пластичности материала.
как и прежде, ресурс пластичности материала. Далее следует этап стабильного(контролируемого) роста трещины (это означает, что определенной нагрузкесоответствует фиксированный текущий размер трещины, иными словами, на этом этапе ее рост можно приостановить). Нелинейность упомянутой диаграммы определяется разного родаснижающими жесткость системы факторами – физического (пластическое деформирование) и геометрического (подрастание трещины) характера.
Далее следует этап стабильного(контролируемого) роста трещины (это означает, что определенной нагрузкесоответствует фиксированный текущий размер трещины, иными словами, на этом этапе ее рост можно приостановить). Нелинейность упомянутой диаграммы определяется разного родаснижающими жесткость системы факторами – физического (пластическое деформирование) и геометрического (подрастание трещины) характера. при той же нагрузке. На рис. 4.28 показана схема определения усилия FQ: точка пересечения луча I, проведенного из начала координат под углом a 1, таким, что tg a 1 = 0,95 tg a, с экспериментальной кривой определяет величину расчетной разрушающей нагрузки FQ. Обратите внимание, что данное условие касается тангенса угла a 1, а не самого угла. Как видно, вспомогательный луч II с углом наклона a следует линейному участку диаграммы и отвечает как геометрически, так и физически линейному поведению объекта.
при той же нагрузке. На рис. 4.28 показана схема определения усилия FQ: точка пересечения луча I, проведенного из начала координат под углом a 1, таким, что tg a 1 = 0,95 tg a, с экспериментальной кривой определяет величину расчетной разрушающей нагрузки FQ. Обратите внимание, что данное условие касается тангенса угла a 1, а не самого угла. Как видно, вспомогательный луч II с углом наклона a следует линейному участку диаграммы и отвечает как геометрически, так и физически линейному поведению объекта.
 Таблица 4.1
Таблица 4.1

 Пример 4.1. В результате испытания на вязкость разрушения компактного
Пример 4.1. В результате испытания на вязкость разрушения компактного  ,вычислим критическое значение КИН
,вычислим критическое значение КИН
 и сравним с ней толщину образца Н: 25 > 22,3 мм – в образце обеспечено плоское деформированное состояние – и критическую длину трещины lc: 10 < 22,3 мм – трещина оказалась недостаточно «длинной», т.е., размер зоны пластичности слишком велик по сравнению с длиной трещины, а, значит, все использованные соотношения ЛМР неприменимы.
и сравним с ней толщину образца Н: 25 > 22,3 мм – в образце обеспечено плоское деформированное состояние – и критическую длину трещины lc: 10 < 22,3 мм – трещина оказалась недостаточно «длинной», т.е., размер зоны пластичности слишком велик по сравнению с длиной трещины, а, значит, все использованные соотношения ЛМР неприменимы. представляет собой предел трещиностойкости ихарактеризует лишь трещиностойкость образца из данной стали.
представляет собой предел трещиностойкости ихарактеризует лишь трещиностойкость образца из данной стали.


