Обсуждавшееся до сих пор хрупкое разрушение –лишь один из возможных механизмов исчерпания несущей способности элементов конструкций. Его противоположностью является вязкое разрушение, возможно и без образования трещины. В структурно неоднородных материалах, например, композитах, таких механизмов может больше.
Стремление сформулировать критериальные соотношения, учитывающие оба предельных механизма, а также промежуточные состояния (так называемое квазихрупкое разрушение) было реализовано в виде специальных двухпараметрических критериев. Один их них базируется на концепции коэффициента интенсивности напряжений, другой – раскрытия в вершине трещины (в рамках деформационного подхода). Остановимся на первом, предложенном в свое время Е.М. Морозовым.
В тех условиях, когда реализуется хрупкое разрушение, применим силовой критерий


В этом случае, как уже говорилось, размер зоны пластичности в вершине трещины мал, невелика и критическая нагрузка Fc (рис. 4.31).
 С уменьшением размера трещины величина Fc, очевидно, будет увеличиваться, соответственно увеличивается и зона пластичности.В пределе при l = 0 и нагрузке F В= F (s В) пластическим течением будет охвачено все сечение.Условие вязкого разрушения в этих условиях вполне очевидно:
С уменьшением размера трещины величина Fc, очевидно, будет увеличиваться, соответственно увеличивается и зона пластичности.В пределе при l = 0 и нагрузке F В= F (s В) пластическим течением будет охвачено все сечение.Условие вязкого разрушения в этих условиях вполне очевидно:
 .
.
| Рис. 4.32. Предельная поверхность модельного материала в котором возможна реализация либо хрупкого,либо вязкого разрушения
| Рис. 4.33. Предельная поверхность реального материала в котором возможны как хрупкоеили вязкое, так и смешаноеразрушения
|
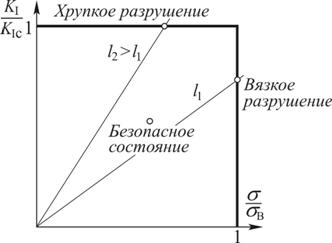
 Допустим, что в образце могут реализовываться только два предельных механизма – хрупкое и вязкое разрушение – в отсутствии смешаных. Отвечающая обоим критериям предельная поверхность такого модельного материала показана на рис. 4.32. Критерий достижения предельного состояния в двухпараметрической форме имеет вид
Допустим, что в образце могут реализовываться только два предельных механизма – хрупкое и вязкое разрушение – в отсутствии смешаных. Отвечающая обоим критериям предельная поверхность такого модельного материала показана на рис. 4.32. Критерий достижения предельного состояния в двухпараметрической форме имеет вид


Приведенная схема является предельно упрощенной и носит иллюстративный характер. В действительности всегда имеют место смешаные виды разрушения, поэтому предельная поверхность уже не имеетпрямых граней (рис. 4.33).
Эксперименты и теоретический анализ показывают, что в бесконечной пластине с увеличением длины трещины lc происходит компенсирующее падение разрушающей нагрузки sс, в результате чего критическое значение K (lc, sс) КИН остается постоянным. Линия предельной поверхности в области хрупких разрушений оказывается параллельна оси абсцисс (см. рис. 4.33); и вообще, если для данного материала в рассматриваемых условиях существует возможность хрупкого разрушения, то предельная поверхность будет иметь горизонтальное плато.
В телах конечных размеров КИН определяется, помимо прочего,еще и взаимодействием поля напряжений в вершине трещины с границами объекта (в частности, для схемы, изображенной на рис. 4.31  ,см. также рис. 4.10); в
,см. также рис. 4.10); в  этих условиях взаимная компенсация величин sс и lc в широких пределах уженевозможна, поэтому критическое значение КИН оказывается зависимым от длины трещины lc (отражается поверхностью разрушения–сплошной линией на рис. 4.33).
этих условиях взаимная компенсация величин sс и lc в широких пределах уженевозможна, поэтому критическое значение КИН оказывается зависимым от длины трещины lc (отражается поверхностью разрушения–сплошной линией на рис. 4.33).
Сама же зависимость
K (l, sс) = Kс (l),
найденная экспериментально с помощью соотношений линейной механики разрушения, была названа автором пределом трещиностойкости (Ic).
Надо признать, что это обстоятельство – зависимость отразмера трещины – затрудняет определение характеристики Ic. Ниже будет показано, что в определенном диапазоне длин трещин (длинных трещин) предел трещиностойкости можно считать почти независимым от параметра l.
Не случайно вэтом разделе столько внимания было уделено силовому подходу в механике разрушения – именно он, главным образом, используется в практике инженерных расчетов, связанных соценкой трещиностойкости конструкций. Вместе с тем, наряду ссиловым в механике разрушения разрабатываются и иные, альтернативные, подходы – энергетический и деформационный, которые более распространены в научной практике.
Энергетический подход
 к оценке трещиностойкостиэлементов конструкций
к оценке трещиностойкостиэлементов конструкций
Другими довольно широко используемыми в настоящее времякритериями трещиностойкости элементов конструкций являются энергетические. Смысл энергетического подхода к формулировке условия хрупкого разрушения состоит в следующем:
рост трещины возможен лишь в том случае, когда система способна выделить энергию, необходимую для образования новых поверхностей.
Источником энергии может быть работа, совершаемая внешней нагрузкой, или энергия упругого деформирования, запасенная в системе.
Стабильный (контролируемый, см. рис. 4.28) рост трещины в пластине единичной толщины возможен, если выполняется условие
 , ,
| (4.7)
|
где А – работа внешней нагрузки; 
U – потенциальная энергия упругого деформирования;
F – энергия, необходимая для образования новых поверхностей, иными словами, для продвижения трещины.
Структура энергозатрат на этапе стабильного роста трещины показана на рис. 4.23.
Параметр  называется интенсивностью выделения энергии,
называется интенсивностью выделения энергии,  – сопротивлением росту трещины.
– сопротивлением росту трещины.
По смыслу отношение  представляет собой энергию, приходящуюся на единицу пути распространения трещины, которая пропорциональна величине
представляет собой энергию, приходящуюся на единицу пути распространения трещины, которая пропорциональна величине  ; интенсивность же выделения энергии в целом –
; интенсивность же выделения энергии в целом – 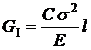 . Схеме «трещина в бесконечной тонкой пластине при одноосном растяжении» (рис. 4.7) соответствует значение постоянной С = p; окончательно
. Схеме «трещина в бесконечной тонкой пластине при одноосном растяжении» (рис. 4.7) соответствует значение постоянной С = p; окончательно
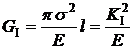
| – плоское напряженное состояние;
| (4.8)
|

| –плоскоедеформированноесостояние.
| (4.9)
|
Таким образом, для стабильного роста трещины необходим баланс между подводимой и поглощаемой энергией. В хрупких материалах, таких как силикатное стекло, полиметилметакрилат, конструкционная керамика и др., последнюю связывают с так называемой поверхностной энергиейg, необходимой для образования новых поверхностей,
F = 2 g l,  .
.
Уравнение энергетического баланса (4.7) для системы на рис. 4.7 разрешим относительно критического напряжения sc:
 .
.
Этот критерий впервые был сформулирован А.Гриффитсом.
Анализ и экспериментальные проверки критерия Гриффитса (Ирвин, Орован и др.) показали, что в действительности энергия развития трещины в металлах значительно превосходит теоретическую величинуповерхностной энергии g. Этот факт объясняется преобладанием в общих энергетических затратах доли энергии, расходуемой на пластическое деформирование материала у вершины трещины(диссипации), над той ее частью, которая необходима непосредственно для  разделения поверхностей, т.е., разрушения, разрыва связей в материале.
разделения поверхностей, т.е., разрушения, разрыва связей в материале.
В результате экспериментальных исследований было установлено, что сопротивление росту трещины R при плоском деформированном состоянии практически не зависит от ее длины l. Существует такое значение интенсивности выделения энергии  – константа материала, выше которого материал не способен поглотить выделяемую системой энергию (рис. 4.34). Условие энергетического баланса нарушается: G > R – стабильное подрастание трещины сменяется лавинообразным.
– константа материала, выше которого материал не способен поглотить выделяемую системой энергию (рис. 4.34). Условие энергетического баланса нарушается: G > R – стабильное подрастание трещины сменяется лавинообразным.
В условиях плоского напряженного состояния характеристика R=R (l)нелинейна, в связи с чем она получила название R–кривая. Как следует из схемы нарис. 4.34 справа, при любой величине номинального напряжения s £ s 2рост трещины невозможен, поскольку выделяемой энергии недостаточно для преодоления сопротивления росту трещины(равенство G = R выполняется в одной-единственной точке – В); тем не менее размер трещины в этот момент, как и во все предыдущие, остается прежним(Dli =0). По мере увеличения нагрузки s > s 2происходит контролируемый рост трещины, так напряжению s 3отвечает удлинение D l 3.Наконец, точка D на диаграмме соответствует моменту, после которого энергетический баланс нарушается в пользу интенсивности выделения энергии (G > R), стабильный рост трещины сменяется нестабильным.
Таким образом, необходимое и достаточное условие разрушения в энергетических терминах имеет вид
 G = R;
G = R;
 .
.
Заметим, что при плоском напряженном состоянии критическая интенсивностьвыделения энергии G 1с уже не является характеристикой материала.
 Крафт предположил, что для данного элемента конструкции R –кривая инвариантна по отношению к длине трещины, что для определенных условий было подтверждено экспериментально. На основании этой гипотезы можно любой длине li трещины сопоставить значение характеристики трещиностойкости
Крафт предположил, что для данного элемента конструкции R –кривая инвариантна по отношению к длине трещины, что для определенных условий было подтверждено экспериментально. На основании этой гипотезы можно любой длине li трещины сопоставить значение характеристики трещиностойкости  (рис. 4.35).
(рис. 4.35).



 В ходе экспериментального изучения закономерностей распространения трещин в плоских образцах в ряде случаевотмечалась локальная нестабильность этого процесса.Сростом нагрузки трещина, вначале неподвижная, при достижении некоего порогового значения интенсивности выделения упругой энергии
В ходе экспериментального изучения закономерностей распространения трещин в плоских образцах в ряде случаевотмечалась локальная нестабильность этого процесса.Сростом нагрузки трещина, вначале неподвижная, при достижении некоего порогового значения интенсивности выделения упругой энергии  , не зависящего от длины трещины, совершает резкий скачок на величину D lхлопка (рис. 4.36), сопровождающийся отчетливо слышимым щелчком, после чего следует период ее стабильного развития.
, не зависящего от длины трещины, совершает резкий скачок на величину D lхлопка (рис. 4.36), сопровождающийся отчетливо слышимым щелчком, после чего следует период ее стабильного развития.  Эта особенность получила название«эффект хлопка».Для описания эффекта хлопка были предложены специального вида R –кривые, одна из которых приведена на рис. 4.36.
Эта особенность получила название«эффект хлопка».Для описания эффекта хлопка были предложены специального вида R –кривые, одна из которых приведена на рис. 4.36.
 Своеобразной характеристикой трещиностойкости конкретногообъекта можно считать упоминаемую ранее довольно часто в отечественной и зарубежной литературе диаграмму докритического разрушения –связь номинального напряжения, по сути, нагрузки, с длиной трещины на стадии ее стабильного развития (рис. 4.37). Нетрудно видеть, что данная диаграмма может бытьполученапутем анализа поведения трещины в указанный период, и полностью объясняется соотношениемфункции G (s, l)и заданной R –кривой.
Своеобразной характеристикой трещиностойкости конкретногообъекта можно считать упоминаемую ранее довольно часто в отечественной и зарубежной литературе диаграмму докритического разрушения –связь номинального напряжения, по сути, нагрузки, с длиной трещины на стадии ее стабильного развития (рис. 4.37). Нетрудно видеть, что данная диаграмма может бытьполученапутем анализа поведения трещины в указанный период, и полностью объясняется соотношениемфункции G (s, l)и заданной R –кривой.


Ранее, в подразделе 4.9 было отмечено, что для достаточно длинных трещин предел трещиностойкостидовольно слабозависит от параметра l, и в первом приближенииего можно считать постоянным.Это утверждение иллюстрирует рис. 4.37: критические длины трещины lс, lс 1, lс 2 заметно отличаются друг от друга,но критическая интенсивность выделения упругой энергии  с ростом длины трещины увеличивается незначительно. Таким образом, задавшись допуском DG 1c, можно определить диапазон длин трещин, в котором величина G 1cстановится постоянной рассматриваемой системы, чтоупрощает соответствующие расчеты.
с ростом длины трещины увеличивается незначительно. Таким образом, задавшись допуском DG 1c, можно определить диапазон длин трещин, в котором величина G 1cстановится постоянной рассматриваемой системы, чтоупрощает соответствующие расчеты.


 В пластинах конечной ширины (так называемых полосах) зависи
В пластинах конечной ширины (так называемых полосах) зависи  мость G (l) становится нелинейной (рис. 4.35, трещинадлинойот
мость G (l) становится нелинейной (рис. 4.35, трещинадлинойот  ) в связи со взаимодействием поля напряжений в вершине с границами пластины. С учетомоднозначной связи между параметрами G и K в рамках линейной механики разрушения (см. соотношения (4.8), (4.9))это обстоятельство отражается введением в выражение для коэффициента интенсивности напряжений корректирующих функций, например,
) в связи со взаимодействием поля напряжений в вершине с границами пластины. С учетомоднозначной связи между параметрами G и K в рамках линейной механики разрушения (см. соотношения (4.8), (4.9))это обстоятельство отражается введением в выражение для коэффициента интенсивности напряжений корректирующих функций, например,

(см. подраздел 4.4). В связи с этим кривая  имеет экстремум (рис. 4.38).Оказывается, наибольшая трещиностойкость пластин с трещинами может быть достигнута при оптимальном с точки зрения хрупкой прочности соотношении ширины пластины и длины трещины, причем, надо заметить, не самой короткой.
имеет экстремум (рис. 4.38).Оказывается, наибольшая трещиностойкость пластин с трещинами может быть достигнута при оптимальном с точки зрения хрупкой прочности соотношении ширины пластины и длины трещины, причем, надо заметить, не самой короткой.
 В том случае, когда размер зоны пластичности не может считаться весьма малым по сравнению с длиной трещины (необходимо отличие, по крайней мере, в 25 раз, см. подраздел 4.7), параметр «интенсивность выделения упругой энергии» неприменим, т.к. пренебречь диссипацией энергии при неупругом деформировании уже нельзя. Решения задачи о напряженно-деформированном состоянии в окрестности трещины, выходящее за рамки линейной механики разрушения, были предложены независимоГ.П. Черепановым и Дж. Райсом. Последним также был сформулирован энергетический критерий разрушения, использующий специальную характеристику – так называемый J – интеграл
В том случае, когда размер зоны пластичности не может считаться весьма малым по сравнению с длиной трещины (необходимо отличие, по крайней мере, в 25 раз, см. подраздел 4.7), параметр «интенсивность выделения упругой энергии» неприменим, т.к. пренебречь диссипацией энергии при неупругом деформировании уже нельзя. Решения задачи о напряженно-деформированном состоянии в окрестности трещины, выходящее за рамки линейной механики разрушения, были предложены независимоГ.П. Черепановым и Дж. Райсом. Последним также был сформулирован энергетический критерий разрушения, использующий специальную характеристику – так называемый J – интеграл
 ;
;
здесь Ti = sij nj – составляющие проекции тензора напряжения на нормаль к замкнутому контуру Г (рис. 4.39);


 – работа, затраченная на деформирование элемента объема;
– работа, затраченная на деформирование элемента объема;
u – перемещение вдоль оси х;
ds – элемент дуги контура Г.
 Можно показать, что J –интег-рал не зависит от пути интегрирования (поэтому его называют контурно независимым) при условии, что контур интегрирования не вторгается в зону пластического деформирования. Это позволяет выбирать такие траектории, где интегрирование не представляет трудностей, например, свободные края образца (рис. 4.39).
Можно показать, что J –интег-рал не зависит от пути интегрирования (поэтому его называют контурно независимым) при условии, что контур интегрирования не вторгается в зону пластического деформирования. Это позволяет выбирать такие траектории, где интегрирование не представляет трудностей, например, свободные края образца (рис. 4.39).

 В тех условиях, когда справедлив подход линейной механики разрушения, J –интеграл совпадает с интенсивностью выделения упругой энергии G, в общем же случае величина
В тех условиях, когда справедлив подход линейной механики разрушения, J –интеграл совпадает с интенсивностью выделения упругой энергии G, в общем же случае величина  (U –потенциальная энергия) представляет обобщенную функцию выделения энергии системой за счет продвижения трещины (рис. 4.40). Аналогом критического значения G 1 с является критическое значение J –интеграла J 1 с , что экспериментально было подтверждено Бигли, Лэндисом, Кобаяши и др.
(U –потенциальная энергия) представляет обобщенную функцию выделения энергии системой за счет продвижения трещины (рис. 4.40). Аналогом критического значения G 1 с является критическое значение J –интеграла J 1 с , что экспериментально было подтверждено Бигли, Лэндисом, Кобаяши и др.







 С уменьшением размера трещины величина Fc, очевидно, будет увеличиваться, соответственно увеличивается и зона пластичности.В пределе при l = 0 и нагрузке F В= F (s В) пластическим течением будет охвачено все сечение.Условие вязкого разрушения в этих условиях вполне очевидно:
С уменьшением размера трещины величина Fc, очевидно, будет увеличиваться, соответственно увеличивается и зона пластичности.В пределе при l = 0 и нагрузке F В= F (s В) пластическим течением будет охвачено все сечение.Условие вязкого разрушения в этих условиях вполне очевидно: .
.
 Допустим, что в образце могут реализовываться только два предельных механизма – хрупкое и вязкое разрушение – в отсутствии смешаных. Отвечающая обоим критериям предельная поверхность такого модельного материала показана на рис. 4.32. Критерий достижения предельного состояния в двухпараметрической форме имеет вид
Допустим, что в образце могут реализовываться только два предельных механизма – хрупкое и вязкое разрушение – в отсутствии смешаных. Отвечающая обоим критериям предельная поверхность такого модельного материала показана на рис. 4.32. Критерий достижения предельного состояния в двухпараметрической форме имеет вид

 ,см. также рис. 4.10); в
,см. также рис. 4.10); в  к оценке трещиностойкостиэлементов конструкций
к оценке трещиностойкостиэлементов конструкций ,
,
 называется интенсивностью выделения энергии,
называется интенсивностью выделения энергии,  – сопротивлением росту трещины.
– сопротивлением росту трещины. представляет собой энергию, приходящуюся на единицу пути распространения трещины, которая пропорциональна величине
представляет собой энергию, приходящуюся на единицу пути распространения трещины, которая пропорциональна величине  ; интенсивность же выделения энергии в целом –
; интенсивность же выделения энергии в целом – 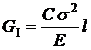 . Схеме «трещина в бесконечной тонкой пластине при одноосном растяжении» (рис. 4.7) соответствует значение постоянной С = p; окончательно
. Схеме «трещина в бесконечной тонкой пластине при одноосном растяжении» (рис. 4.7) соответствует значение постоянной С = p; окончательно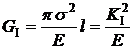

 .
. .
. – константа материала, выше которого материал не способен поглотить выделяемую системой энергию (рис. 4.34). Условие энергетического баланса нарушается: G > R – стабильное подрастание трещины сменяется лавинообразным.
– константа материала, выше которого материал не способен поглотить выделяемую системой энергию (рис. 4.34). Условие энергетического баланса нарушается: G > R – стабильное подрастание трещины сменяется лавинообразным. G = R;
G = R; .
. Крафт предположил, что для данного элемента конструкции R –кривая инвариантна по отношению к длине трещины, что для определенных условий было подтверждено экспериментально. На основании этой гипотезы можно любой длине li трещины сопоставить значение характеристики трещиностойкости
Крафт предположил, что для данного элемента конструкции R –кривая инвариантна по отношению к длине трещины, что для определенных условий было подтверждено экспериментально. На основании этой гипотезы можно любой длине li трещины сопоставить значение характеристики трещиностойкости  (рис. 4.35).
(рис. 4.35).


 , не зависящего от длины трещины, совершает резкий скачок на величину D lхлопка (рис. 4.36), сопровождающийся отчетливо слышимым щелчком, после чего следует период ее стабильного развития.
, не зависящего от длины трещины, совершает резкий скачок на величину D lхлопка (рис. 4.36), сопровождающийся отчетливо слышимым щелчком, после чего следует период ее стабильного развития.  Своеобразной характеристикой трещиностойкости конкретногообъекта можно считать упоминаемую ранее довольно часто в отечественной и зарубежной литературе диаграмму докритического разрушения –связь номинального напряжения, по сути, нагрузки, с длиной трещины на стадии ее стабильного развития (рис. 4.37). Нетрудно видеть, что данная диаграмма может бытьполученапутем анализа поведения трещины в указанный период, и полностью объясняется соотношениемфункции G (s, l)и заданной R –кривой.
Своеобразной характеристикой трещиностойкости конкретногообъекта можно считать упоминаемую ранее довольно часто в отечественной и зарубежной литературе диаграмму докритического разрушения –связь номинального напряжения, по сути, нагрузки, с длиной трещины на стадии ее стабильного развития (рис. 4.37). Нетрудно видеть, что данная диаграмма может бытьполученапутем анализа поведения трещины в указанный период, и полностью объясняется соотношениемфункции G (s, l)и заданной R –кривой.



 В пластинах конечной ширины (так называемых полосах) зависи
В пластинах конечной ширины (так называемых полосах) зависи  ) в связи со взаимодействием поля напряжений в вершине с границами пластины. С учетомоднозначной связи между параметрами G и K в рамках линейной механики разрушения (см. соотношения (4.8), (4.9))это обстоятельство отражается введением в выражение для коэффициента интенсивности напряжений корректирующих функций, например,
) в связи со взаимодействием поля напряжений в вершине с границами пластины. С учетомоднозначной связи между параметрами G и K в рамках линейной механики разрушения (см. соотношения (4.8), (4.9))это обстоятельство отражается введением в выражение для коэффициента интенсивности напряжений корректирующих функций, например,
 имеет экстремум (рис. 4.38).Оказывается, наибольшая трещиностойкость пластин с трещинами может быть достигнута при оптимальном с точки зрения хрупкой прочности соотношении ширины пластины и длины трещины, причем, надо заметить, не самой короткой.
имеет экстремум (рис. 4.38).Оказывается, наибольшая трещиностойкость пластин с трещинами может быть достигнута при оптимальном с точки зрения хрупкой прочности соотношении ширины пластины и длины трещины, причем, надо заметить, не самой короткой. В том случае, когда размер зоны пластичности не может считаться весьма малым по сравнению с длиной трещины (необходимо отличие, по крайней мере, в 25 раз, см. подраздел 4.7), параметр «интенсивность выделения упругой энергии» неприменим, т.к. пренебречь диссипацией энергии при неупругом деформировании уже нельзя. Решения задачи о напряженно-деформированном состоянии в окрестности трещины, выходящее за рамки линейной механики разрушения, были предложены независимоГ.П. Черепановым и Дж. Райсом. Последним также был сформулирован энергетический критерий разрушения, использующий специальную характеристику – так называемый J – интеграл
В том случае, когда размер зоны пластичности не может считаться весьма малым по сравнению с длиной трещины (необходимо отличие, по крайней мере, в 25 раз, см. подраздел 4.7), параметр «интенсивность выделения упругой энергии» неприменим, т.к. пренебречь диссипацией энергии при неупругом деформировании уже нельзя. Решения задачи о напряженно-деформированном состоянии в окрестности трещины, выходящее за рамки линейной механики разрушения, были предложены независимоГ.П. Черепановым и Дж. Райсом. Последним также был сформулирован энергетический критерий разрушения, использующий специальную характеристику – так называемый J – интеграл ;
;

 Можно показать, что J –интег-рал не зависит от пути интегрирования (поэтому его называют контурно независимым) при условии, что контур интегрирования не вторгается в зону пластического деформирования. Это позволяет выбирать такие траектории, где интегрирование не представляет трудностей, например, свободные края образца (рис. 4.39).
Можно показать, что J –интег-рал не зависит от пути интегрирования (поэтому его называют контурно независимым) при условии, что контур интегрирования не вторгается в зону пластического деформирования. Это позволяет выбирать такие траектории, где интегрирование не представляет трудностей, например, свободные края образца (рис. 4.39).
 В тех условиях, когда справедлив подход линейной механики разрушения, J –интеграл совпадает с интенсивностью выделения упругой энергии G, в общем же случае величина
В тех условиях, когда справедлив подход линейной механики разрушения, J –интеграл совпадает с интенсивностью выделения упругой энергии G, в общем же случае величина  (U –потенциальная энергия) представляет обобщенную функцию выделения энергии системой за счет продвижения трещины (рис. 4.40). Аналогом критического значения G 1 с является критическое значение J –интеграла J 1 с , что экспериментально было подтверждено Бигли, Лэндисом, Кобаяши и др.
(U –потенциальная энергия) представляет обобщенную функцию выделения энергии системой за счет продвижения трещины (рис. 4.40). Аналогом критического значения G 1 с является критическое значение J –интеграла J 1 с , что экспериментально было подтверждено Бигли, Лэндисом, Кобаяши и др.

