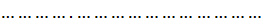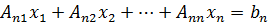Введение
Математика играет важную роль в исследовании различных физических объектов, представляя собой по сути «язык» любой физической теории. Без использования этого специального языка изложение теории электромагнитного поля было бы весьма затруднительно, не говоря уже о применении теории электромагнетизма в практических приложениях.
В данном пособии излагаются математические сведения, необходимые для последующего изучения курса «Электромагнитные поля и волны». Будут изложены вопросы, частично знакомые вам в результате предшествующих курсов математики, однако их более глубокое изучение представляется весьма полезным.
Это касается теории векторных полей, векторных дифференциальных операторов, дифференциальных уравнений с частными производными, некоторых методов математической физики, теории гармонических колебаний, волновых уравнений, краевых задач электродинамики и вычислительных методов.
Глава 1. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
Физические величины могут характеризоваться не только их числовым значением (например, масса, температура) – тогда они называются скалярами, но и направлением в пространстве (например, скорость, сила). Такие величины называются векторами. К этому классу физических величин относятся и характеристики электромагнитного поля - напряжённости, изучаемые в курсе электродинамики. Поэтому эти характеристики описываются с помощью математической теории векторных полей.
Векторы и действия над ними
1.1 Основные операции. Произвольный вектор 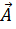 можно представить как
можно представить как 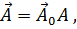 где
где 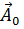 - единичный вектор (орт), а A - абсолютное значение вектора
- единичный вектор (орт), а A - абсолютное значение вектора 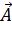 . Орты, соответствующие направлениям осей декартовой системы координат, будем обозначать
. Орты, соответствующие направлениям осей декартовой системы координат, будем обозначать 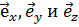 . Таким образом, в проекциях на эти оси вектор
. Таким образом, в проекциях на эти оси вектор 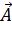 имеет следующий вид:
имеет следующий вид:
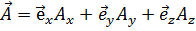 . (1.1)
. (1.1)
Проекции вектора 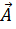 на оси координат
на оси координат 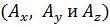 называются также его компонентами, или составляющими вектора.
называются также его компонентами, или составляющими вектора.
Сложение в векторной алгебре понимается как алгебраическое сложение компонент векторов:
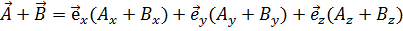 . (1.2)
. (1.2)
Умножение вектора 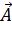 на число (скаляр) m есть получение вектора
на число (скаляр) m есть получение вектора
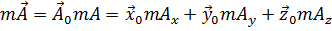 (1.3)
(1.3)
с новым абсолютным значением | m | A.
Скалярное произведение векторов 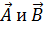 обозначается
обозначается 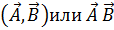 и определяется следующим образом:
и определяется следующим образом:
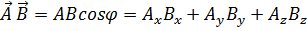 , (1.4)
, (1.4)
где 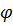 - угол между направлениями векторов. В результате скалярного произведения векторов образуется число. Как видно из (1.4), значение скалярного произведения может быть равным нулю при равных нулю исходных векторах
- угол между направлениями векторов. В результате скалярного произведения векторов образуется число. Как видно из (1.4), значение скалярного произведения может быть равным нулю при равных нулю исходных векторах 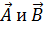 (т.е. векторах с ненулевыми значениями A и B), либо при нулевых значениях
(т.е. векторах с ненулевыми значениями A и B), либо при нулевых значениях 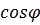 . В последнем случае эти векторы называются ортогональными: они направлены под прямым углом друг к другу.
. В последнем случае эти векторы называются ортогональными: они направлены под прямым углом друг к другу.
Векторное произведение векторов 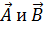 , обозначаемое
, обозначаемое 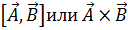 есть
есть
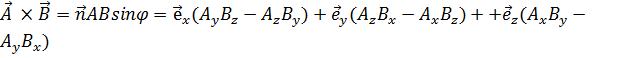 , (1.5)
, (1.5)
где 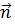 - единичный вектор, направленный по нормали к плоскости векторов
- единичный вектор, направленный по нормали к плоскости векторов 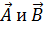 , причем так, что
, причем так, что 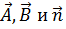 образуют «правую тройку» векторов: если смотреть вдоль
образуют «правую тройку» векторов: если смотреть вдоль 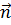 , то кратчайшее угловое расстояние между векторами
, то кратчайшее угловое расстояние между векторами 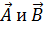 , обозначенное φ, будет соответствовать движению от
, обозначенное φ, будет соответствовать движению от 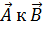 по часовой стрелке. Удобно записывать векторное произведение в форме следующего определителя:
по часовой стрелке. Удобно записывать векторное произведение в форме следующего определителя:
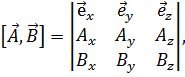 (1.5a)
(1.5a)
раскрытие которого приводит к указанному результату. Векторное произведение некоммутативно, т.е. сомножители нельзя переставлять местами, имея в виду сохранение результата. А именно:
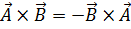 .(1.6)
.(1.6)
Под векторно-скалярным (смешанным) произведением векторов  понимается скаляр
понимается скаляр 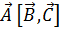 ; при этом
; при этом
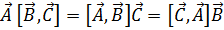 , (1.7).
, (1.7).
т. е. важен циклический порядок следования перемножаемых векторов 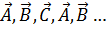 , при сохранении которого безразлично, какие два вектора из трёх образуют векторное произведение. На основании (1.4) и (1.5) легко установить, что
, при сохранении которого безразлично, какие два вектора из трёх образуют векторное произведение. На основании (1.4) и (1.5) легко установить, что
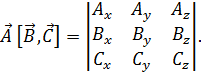 (1.8)
(1.8)
Далее, запишем формулу двойного векторного произведения:
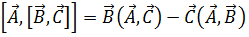 (1.9)
(1.9)
1.2. Линейное преобразование векторов.Вернёмся к вопросу обумножении вектора на скаляр. Согласно (1.3), равенство векторов
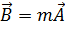 (1.10)
(1.10)
равносильно трем скалярным равенствам:
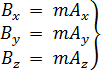 , (1.10а)
, (1.10а)
Если m - положительное число, то векторы 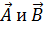 направлены одинаково, а при отрицательном m - противоположно («параллельно» и «антипараллельно»); говорят, что такие векторы
направлены одинаково, а при отрицательном m - противоположно («параллельно» и «антипараллельно»); говорят, что такие векторы 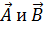 коллинеарны. Мы имеем здесь дело с частным видом линейного преобразования набора компонент
коллинеарны. Мы имеем здесь дело с частным видом линейного преобразования набора компонент 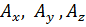 в аналогичный набор
в аналогичный набор 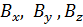 ; заметим, что эти совокупности компонент, вполне определяющие векторы
; заметим, что эти совокупности компонент, вполне определяющие векторы 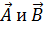 , мы также можем называть векторами.
, мы также можем называть векторами.
В общем случае под однородным линейным преобразованием рассматриваемых векторов понимают сопоставление вектору 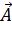 нового вектора
нового вектора 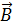 , компоненты которого определяются по формулам:
, компоненты которого определяются по формулам:
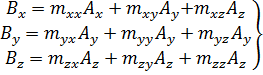 , (1.11)
, (1.11)
где тхх, тху,..., тzу, тzz - некоторые числа. Векторы 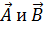 ,компоненты которых связаны соотношениями (1.11), уже не коллинеарны; следовательно, записанное преобразование определяет не только изменение абсолютного значения («растяжение» или «сжатие») вектора, но и некоторый его поворот.
,компоненты которых связаны соотношениями (1.11), уже не коллинеарны; следовательно, записанное преобразование определяет не только изменение абсолютного значения («растяжение» или «сжатие») вектора, но и некоторый его поворот.
Остановимся на формальном описании преобразования (1.11). С точки зрения линейной алгебры, таблица чисел
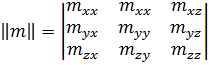 (1.12)
(1.12)
образует матрицу, а равенства (1.11)выражают операцию умножения матрицы 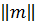 на вектор-столбец (
на вектор-столбец (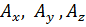 ), приводящую к вектору-столбцу (Вх, Ву, Bz). В частности, в (1.10а) мы имеем случай, когда |
), приводящую к вектору-столбцу (Вх, Ву, Bz). В частности, в (1.10а) мы имеем случай, когда | 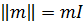 , где
, где
 (1.13)
(1.13)
так называемая единичная матрица.
Вместо символа матрицы 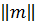 введём иной символ
введём иной символ 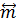 и запишем равенства (1.11) в следующей сокращённой форме:
и запишем равенства (1.11) в следующей сокращённой форме:
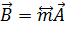 (1.14)
(1.14)
Умножение 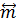 на
на 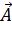 здесь понимается как выполнение операций над компонентами вектора
здесь понимается как выполнение операций над компонентами вектора 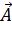 , содержащимися в. (1.11). Соотношение (1.14) есть обобщение равенства векторной алгебры (1.10), в котором роль множителя вместо скаляpa m играет объект более сложного характера
, содержащимися в. (1.11). Соотношение (1.14) есть обобщение равенства векторной алгебры (1.10), в котором роль множителя вместо скаляpa m играет объект более сложного характера 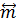 , называемый тензором. В частности, единичной матрице I соответствует также обозначаемый единичный тензор I.
, называемый тензором. В частности, единичной матрице I соответствует также обозначаемый единичный тензор I.
Тензор 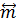 выступает как оператор, который, действуя на вектор
выступает как оператор, который, действуя на вектор 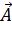 , преобразует его в другой вектор
, преобразует его в другой вектор 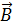 .
.
1.3. Радиус-вектор.Рассмотрим важный пример вектора, зависящего от точки пространства, в которой он рассматривается, т. е. пример векторной функции. Это радиус-вектор 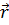 ,
,
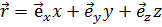 , (1.15)
, (1.15)
который представляет собой направленный отрезок, соединяющий начало координат О (0, 0, 0) с некоторой «текущей» точкой М (х, у, z.). Длина радиус-вектора r = ОМ (его абсолютное значение) есть скалярная функция
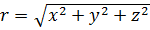 . (1.15а)
. (1.15а)
Очевидно, отрезок, соединяющий две точки Р(х', у', z') и М(х, у, z), изображается разностью их радиус-векторов:
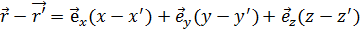 . (1.16)
. (1.16)
Абсолютное значение этого вектора выражает расстояние между точками Р и М:
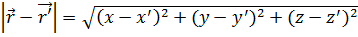 (1.16a)
(1.16a)
Ротор. Теорема Стокса
4.1. Ротор. В 1.2 было показано, что для полей потенциальных циркуляция при однозначности потенциала равна нулю (п. 4). Однако в общем случае циркуляция вектора 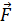 по некоторому контуру L не должна обязательно быть равной нулю. Подобно потоку вектора, циркуляция также может быть использована для локальной характеристики поля. При этом возникает понятие ротора вектора
по некоторому контуру L не должна обязательно быть равной нулю. Подобно потоку вектора, циркуляция также может быть использована для локальной характеристики поля. При этом возникает понятие ротора вектора 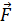 , обозначаемого символом rot
, обозначаемого символом rot 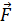 . По определению, rot
. По определению, rot 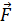 есть вектор, проекция которого на произвольное направление
есть вектор, проекция которого на произвольное направление 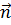 выражается следующим образом:
выражается следующим образом:
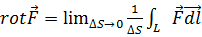 (4.1)
(4.1)
где Δ S - площадка, выбранная так, что 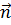 есть нормаль к ней, a L - контур этой площадки, направление обхода которого при интегрировании составляет с нормалью правовинтовую систему (если смотреть вдоль нормали, то обход производится по часовой стрелке).
есть нормаль к ней, a L - контур этой площадки, направление обхода которого при интегрировании составляет с нормалью правовинтовую систему (если смотреть вдоль нормали, то обход производится по часовой стрелке).
4.2. Ротор в декартовых координатах. Как и дивергенцию, ротор вектора нетрудно представить в виде дифференциального выражения в декартовой системе координат. Обратимся к рис. 4.1, на котором через произвольную точку М (х, у, z)проведены три координатные линии и построены элементарные площадки, лежащие в координатных плоскостях. Желая сначала найти проекцию вектора 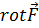 на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)
на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)
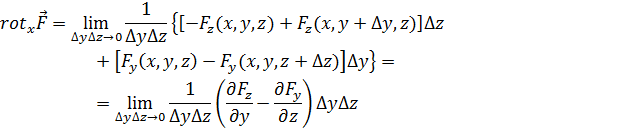
Таким образом,
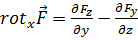 (4.2a)
(4.2a)
Совершенно аналогично получаем:
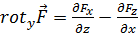 , (4.2б)
, (4.2б)
и
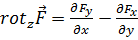 . (4.2в)
. (4.2в)
Эти три равенства удобно объединяются в форме определителя:
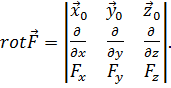 (4.3)
(4.3)
Нетрудно показать, что потенциальные поля являются обязательно «безвихревыми», т. е. для всякого вектора 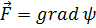 будет
будет 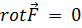 . Чтобы проверить тождество
. Чтобы проверить тождество
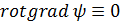 , (4.4)
, (4.4)
достаточно рассмотреть какую-либо одну его проекцию. Так, составляя по формулам (4.2 а)и (2.4 а)проекцию этого вектора на ось х, имеем:
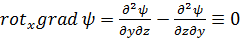 .
.
Другой важный факт заключается в том, что дивергенция вихревого поля тождественно равна нулю, т. е. такое векторное поле соленоидально (3.2):
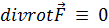 . (4.5)
. (4.5)
Действительно,
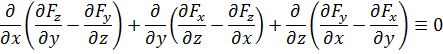
Из определения ротора, его можно трактовать в физическом смысле как вихрь.
4.3. Теорема Стокса. Перейдем, наконец, к теореме Стокса, содержание которой выражается равенством:
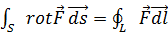 , (4.6)
, (4.6)
где S - некоторая поверхность, a L - её контур, направление обхода которого при интегрировании согласовано с направлением положительной нормали к S, как и ранее. Согласно теореме Стокса, поток ротора некоторого вектора F через поверхность S равен циркуляции самого вектора по соответствующему контуру L.
Чтобы убедиться в справедливости теоремы Стокса, разобьем произвольную поверхность S на достаточно малые элементарные площадки Δ si (рис. 4.3) и для определения ротора 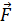 внутри Δs i воспользуемся приближённым соотношением
внутри Δs i воспользуемся приближённым соотношением
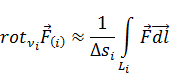
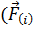 есть
есть 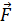 внутри Δ si) вместо (4.1). Поскольку точность этого равенства может быть как угодно велика (достаточно лишь взять соответственно малые размеры элемента Δ si), то
внутри Δ si) вместо (4.1). Поскольку точность этого равенства может быть как угодно велика (достаточно лишь взять соответственно малые размеры элемента Δ si), то
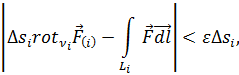
где ε – наперёд заданная сколь угодно малая положительная величина.
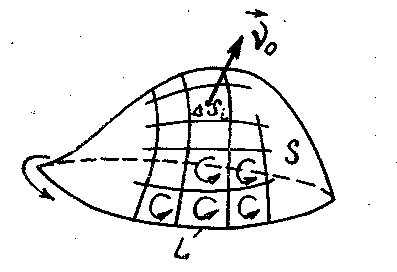
Рис. 4.3
Выбрав все элементы достаточно малыми, произведём суммирование по i и получим:
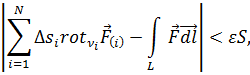
где фигурирует циркуляция 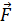 по граничному контуру L всей поверхности S, поскольку при суммировании части циркуляции по общим границам смежных элементов
по граничному контуру L всей поверхности S, поскольку при суммировании части циркуляции по общим границам смежных элементов 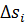 взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.
взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.
Неограниченно измельчая все элементы 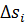 и переходя соответственно этому от суммы к интегралу (N →∞), а также учитывая произвольную малость ε, приходим от предыдущего равенства к формулировке теоремы Стокса (4.6).
и переходя соответственно этому от суммы к интегралу (N →∞), а также учитывая произвольную малость ε, приходим от предыдущего равенства к формулировке теоремы Стокса (4.6).
В сферических координатах
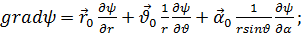 (6.18)
(6.18)
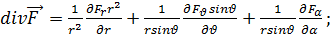 (6.19)
(6.19)
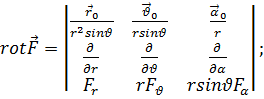 (6.20)
(6.20)
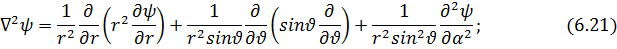
7. О дифференциальных уравнениях
с частными производными
7.1 Уравнения Лапласа и Пуассона.Одним из важнейших средств математической физики является описание процессов при помощи дифференциальных уравнений с частными производными. В отличие от обыкновенных дифференциальных уравнений, содержащих функции одной переменной, в эти уравнения входят функции нескольких переменных. Теория их составляет обширную и сложную область математики, представление о которой невозможно дать в нескольких словах. Однако нельзя пройти мимо того факта, что именно в виде уравнений с частными производными формулируются основные законы электромагнетизма, знакомство с которыми начинается уже в первой главе книги [1].Поэтому ниже излагаются некоторые предварительные сведения о дифференциальных уравнениях математической физики с частными производными.
К распространенным уравнениям математической физики можно придти непосредственно от операций векторного анализа. Так, взяв оператор Лапласа, запишем равенство
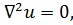 (7.1)
(7.1)
где и - некоторая неизвестная функция пространственных координат. Это уравнение Лапласа. В декартовых координатах (7.1) следует записать как уравнение с частными производными:
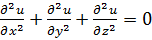 (7.2)
(7.2)
В том случае, когда решение и заведомо не зависит от каких-то двух переменных из трёх (скажем, от у и z), уравнение Лапласа (7.2) переходит в обыкновенное дифференциальное уравнение
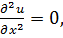 (7.3)
(7.3)
общее решение которого очевидно:
и= Ах + В, (7.4)
(А и В - постоянные). Наличие неопределённых констант, т. е. неопределённость самого решения (7.4), можно истолковать как следствие того факта, что исходное уравнение (7.3) не выражает конкретно очерченной задачи. Такая задача появляется, когда уравнение рассматривается при некоторых дополнительных условиях. Пусть, например, решение уравнения (7.3) ищется в интервале 0 < х < а при следующих условиях:
и (0) = 0 и и (а) = иа.
Вместе с этими условиями уравнение (7.3) составляет так называемую граничную задачу, имеющую единственное решение
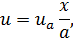
легко получаемое из решения (7.4).
Возвращаясь к уравнению Лапласа (7.1), подчеркнём, что его решение в несравненно более высокой степени неопределённо, чем решение уравнения (7.3). В отличие от обыкновенных дифференциальных уравнений, когда общее решение можно выразить в виде некоторой функции, решения уравнений с частными производными вообще образуют множества («классы») функций. Так всякая функция u, удовлетворяющая в некоторой области V уравнению Лапласа (7.1), называется гармонической в этой области. Если требуется найти и как решение уравнения (7.1) в области V, на границе которой (поверхности S)задана сама функция и или, например, её производная du/dn (возможны и иные граничные условия), то говорят, что поставлена граничная задача для уравнения Лапласа; употребляются также выражения краевые условия, краевая задача.
Уравнение Лапласа, как говорят, является однородным. Соответствующее неоднородное уравнение получаем, записав справа в (7.1) вместо нуля заданную функцию f:
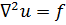 (7.5)
(7.5)
Это так называемое уравнение Пуассона.
7.2. Другие уравнения.Следующее однородное уравнение
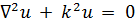 (7.6)
(7.6)
известно под названием уравнения Гельмгольца, или уравнения колебаний. Здесь k2 - постоянная, роль которой в разных случаях различна.
Возьмём случай, в котором ввиду независимости и от у и z уравнение Гельмгольца переходит в известное обыкновенное дифференциальное уравнение
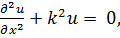 (7.7)
(7.7)
общее решение которого может быть записано в следующих двух формах:
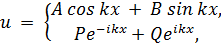 (7.8)
(7.8)
где А, В и Р, Q - константы.
Пусть поставлена граничная задача для уравнения (7.7) наотрезке 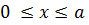 с условиями:
с условиями:
u (0) = 0 и u (а) = 0.
В соответствии с первым граничным условием, мы должны положить в (7.8) А = 0, а согласно второму должно быть ka = mπ (m = 1, 2, 3,...). Поэтому граничная задача имеет следующее множество решений:
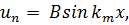
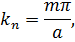
причём m = 1, 2, 3,....; (7.9).
Kаждое решение реализуется при вполне определенном значении постоянной k. Говорят, что решения иm образуют систему собственных функций данной задачи, а km называются соответствующими им собственными значениями.
Записывая справа в (7.6) вместо нуля заданную функцию f, получаем отвечающее уравнению Гельмгольца неоднородное уравнение
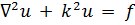 (7.10)
(7.10)
(неоднородное уравнение Гельмгольца). Обычно решения однородного уравнения (7.6) описывают «свободные» (совершающиеся без внешних воздействий) колебания различных систем, а решения неоднородного уравнения (7.10) - «вынужденные» колебания; функция f выражает при этом внешнее воздействие, «вынуждающую силу».
Далее напишем однородное волновое уравнение
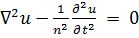 (7.11)
(7.11)
и соответствующее неоднородное уравнение
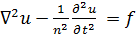 , (7.12)
, (7.12)
называемое уравнением Даламбера. Решение и есть функция координат и времени. Функция f, как и ранее, выражает «вынуждающую силу».
В дальнейшем мы вернемся к обсуждению записанных здесь уравнений математической физики и выясним их роль в теории электромагнетизма. Встретятся и различные уравнения с частными производными относительно векторных функций и, в частности, уравнения типа (7.1), (7.5), (7.6), (7.10) - (7.12).
7.3. Понятие линейности. Обозначив в (7.1) и (7.5) 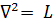 , в (7.6) и (7.10)
, в (7.6) и (7.10) 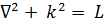 ив (7.11) и (7.12)
ив (7.11) и (7.12) 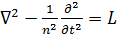 , запишем следующие легко проверяемые равенства:
, запишем следующие легко проверяемые равенства:
L (cu) = cLu,
L (u1 + u2)= Lu1 + Lu2 (7.13)
Здесь L понимают как оператор указанного вида, действующий на некоторую функцию, стоящую за ним справа; с - константа. Равенства (7.13), как принято говорить, выражают свойства линейности рассматриваемых уравнений математической физики.
Согласно (7.13) линейность однородных уравнений (7.1), (7.6), (7.11) означает, что если u1, и2, u3, … - решения какого-нибудь из них, то и линейная комбинация
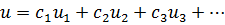
(с1, c2, сз,... - произвольные константы) - также есть решение данного уравнения.
Линейность неоднородных уравнений (7.5), (7.10), (7.12) проявляется в следующем. Пусть f 1, f2, fз, … - различные правые части одного из этих уравнений, при которых оно имеет решения и1, и2, и3, …. Тогда линейная комбинация c1u1 + с2и2 + с3 и3 + … есть решение данного уравнения, в правой части которого стоит аналогичная линейная комбинация (те же константы) соответствующих правых частей:
c1f1 + с2f2 + с3 f3 +....
Линейность рассмотренных уравнений отвечает имеющему большое значение в физике принципу суперпозиции (принципу наложения).
Дельта-функция Дирака
8.1. Первоначальное понятие. Рассмотрим функцию F(x), изображаемую в виде «импульса»:
F(х) = 0 при х < - Δ х и при х > Δ х, причём
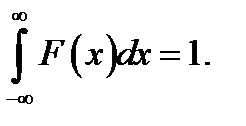 (8.1)
(8.1)
Введём новую функцию δ(х)как предел
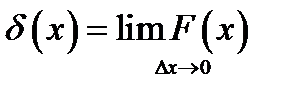 (8.2)
(8.2)
В частности, при задании F(x) в виде прямоугольного импульса она равна:
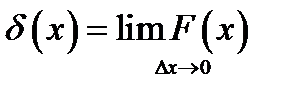
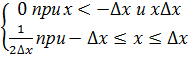 (8.3)
(8.3)
Функция δ (х), как видно, равна нулю везде кроме исчезающе малой окрестности точки х = 0, где она неограниченна. С точки зрения классического математического анализа, рассмотрение δ(х) затруднительно, следовало бы сказать, что предел (8.2), (8.3) не существует.
Тем не менее, произведенные рассуждения наводят на мысль о существовании особого математического объекта, называемого дельта-функцией Дирака (по имени известного физика). В качестве определения дельта-функции δ(х) обычно рассматривают следующее интегральное соотношение
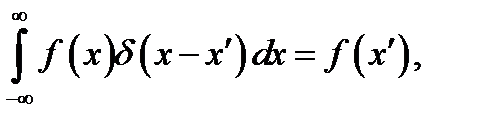 (8.4)
(8.4)
где f(x) - обычная функция. При этом для всякого ограниченного отрезка
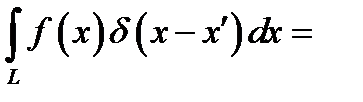
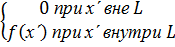 (8.5)
(8.5)
В частности, при f(x) = 1
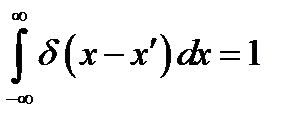 (8.4а)
(8.4а)
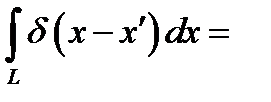
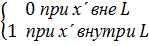 (8.5а)
(8.5а)
Вернёмся теперь к формулам (8.1) - (8.3), чтобы убедиться, что интуитивный образ, к которому они приводят, соответствует определению дельта-функции. Согласно (8.2), (8.3) δ (х)= 0 везде кроме точки х = 0 (соответственно 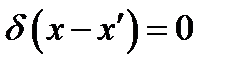 везде кроме точки
везде кроме точки 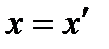 при сохранении интеграла (8.1). Это отвечает соотношениям (8.4 а), (8.5 а). Что касается формул (8.4) и (8.5), то всю область интегрирования, когда она включает точку х΄ можно заменить отрезком ΔL, покрывающим х' и настолько малым, что функцию f(x) на нем можно считать постоянной и равной f(x'). Поэтому
при сохранении интеграла (8.1). Это отвечает соотношениям (8.4 а), (8.5 а). Что касается формул (8.4) и (8.5), то всю область интегрирования, когда она включает точку х΄ можно заменить отрезком ΔL, покрывающим х' и настолько малым, что функцию f(x) на нем можно считать постоянной и равной f(x'). Поэтому
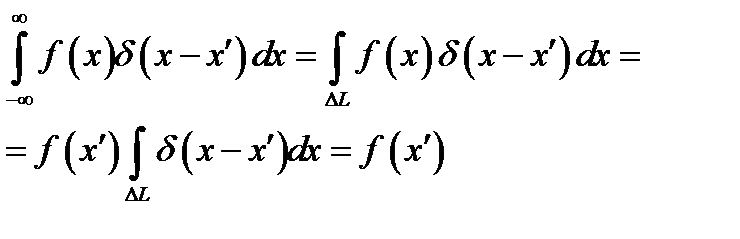 .
.
8.2. Обобщение и примеры. Всё cказанное нетрудно обобщить, например, на функцию трёх переменных. Взяв вместо отрезка L пространственную область V, будем обозначать задаваемые нам функции как /(г) (§ 2, п. 1). Аналогично (8.1) можно рассматривать функцию F(r) такую, что
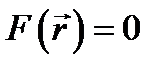 при
при 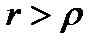
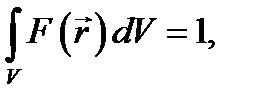
и в том же смысле, что и в (8.2), говорить о предельном случае 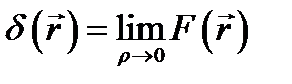
Переходя к определению дельта-функции 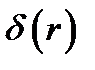 , вместо (8.4) и (8.5) будем иметь:
, вместо (8.4) и (8.5) будем иметь:
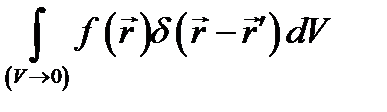 (8.6)
(8.6)
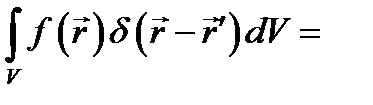
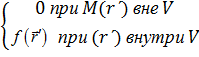 (8.7)
(8.7)
Подобным же образом рассматривается и двумерный случай. Достаточно лишь вместо V взять S; тогда r лежит в плоскости, на которой лежит область S и круг радиуса ρ.
Разумеется, в трехмерном случае (при использовании декартовых координат) справедливо равенство:
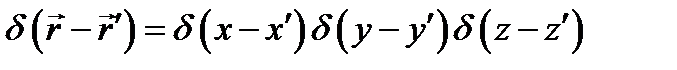 , (8.8)
, (8.8)
и аналогичное равенство можно записать для двумерного случая.
В качество примера применения дельта-функции 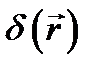 охарактеризуем плотность заряда
охарактеризуем плотность заряда 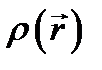 в пространстве при наличии точечного заряда q, расположенного в точке М
в пространстве при наличии точечного заряда q, расположенного в точке М 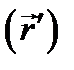 . Легко видеть, что
. Легко видеть, что
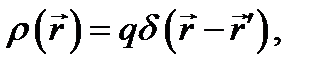 (8.9)
(8.9)
так как при этом
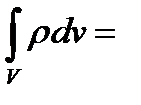
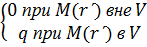 (8.10)
(8.10)
Возьмём, далее, некоторую поверхность S (рис. 8.2), пусть на ней заданы координатные функции q1, q2 (криволинейные координаты, см. п. 6.1) и нормаль  , которую мы представляем как прямолинейную координату с началом на S (n = 0 на S); если S несёт поверхностный заряд с плотностью
, которую мы представляем как прямолинейную координату с началом на S (n = 0 на S); если S несёт поверхностный заряд с плотностью 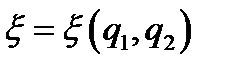 , его можно рассматривать как распределённый в объёме с плотностью
, его можно рассматривать как распределённый в объёме с плотностью
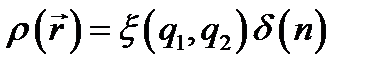 (8.11)
(8.11)
Действительно, 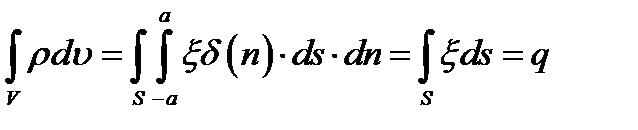
(точки а и - а лежат на прямой n по разные стороны S). Рассмотрим поверхностный ток I, распределенный на Р с плотностью 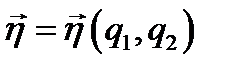 . Вместо
. Вместо 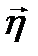 можно ввести плотность тока в объёме
можно ввести плотность тока в объёме
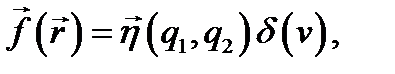 (8.12)
(8.12)
где подразумевается, что точки 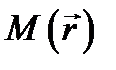 находятся на какой-либо поверхности S, пересекающей Р по линии l, a n - координатная линия в S.
находятся на какой-либо поверхности S, пересекающей Р по линии l, a n - координатная линия в S.
В самом деле, при этом пересекающий 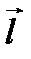 поверхностный ток описывается как ток в объёме с плотностью
поверхностный ток описывается как ток в объёме с плотностью 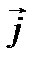 , проходящей через S:
, проходящей через S:
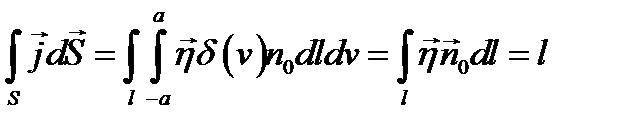
(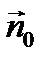 - орт нормали к l, касательный Р).
- орт нормали к l, касательный Р).
Наконец, возьмём случай тока I, протекающего, вдоль, линии L. Для такого линейного тока
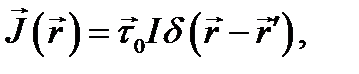 (8.13)
(8.13)
где дельта-функция двумерная; соответственно этому точки 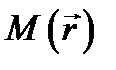 -и
-и 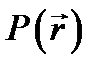 (последняя лежит на L)при интегрировании остаются на какой-либо поверхности, пересекаемой током. Вычисляя ток I, имеем:
(последняя лежит на L)при интегрировании остаются на какой-либо поверхности, пересекаемой током. Вычисляя ток I, имеем:
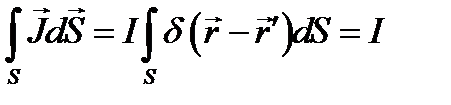
8.3. Представление дельта-функции δ (r).Взявфункцию
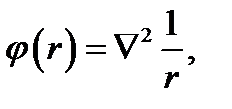
убедимся; что везде, за исключением точки r = 0, она равна нулю. Действительно, на основании (6.21).
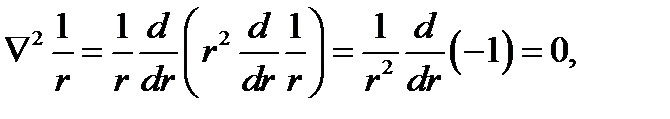
Исследуем теперь объёмный интеграл от  по области V, содержащей начало координат r = 0; при помощи теоремы Остроградского-Гаусса преобразуем его к поверхностному:
по области V, содержащей начало координат r = 0; при помощи теоремы Остроградского-Гаусса преобразуем его к поверхностному:
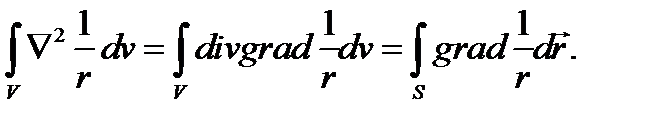
Пусть V - сферический объём с центром при r = 0; тогда S есть соответствующая сферическая поверхность радиуса ρ, на которой функция grad 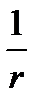 постоянна и согласно (6.18) или (2.12а) равна:
постоянна и согласно (6.18) или (2.12а) равна:
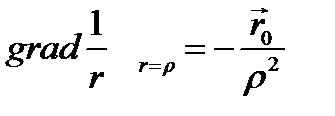
Таким образом, для любого сферического (а, следовательно, и иного) объема V, содержащего начало координат,
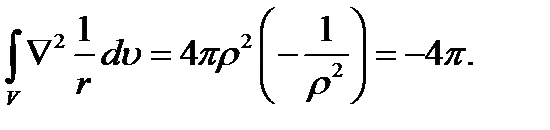
Подведём итог. Функция 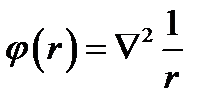 , равная нулю везде, кроме начала координат, при интегрировании по любой области, включающей начало, даёт - 4π. Поэтому, будучи умножена на -1/4π, эта функция удовлетворяет определению (8.6), (8.7). Это значит, что найдена дельта-функция
, равная нулю везде, кроме начала координат, при интегрировании по любой области, включающей начало, даёт - 4π. Поэтому, будучи умножена на -1/4π, эта функция удовлетворяет определению (8.6), (8.7). Это значит, что найдена дельта-функция
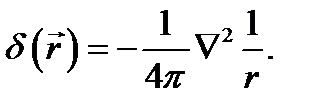 (8.14)
(8.14)
Очевидно также, что
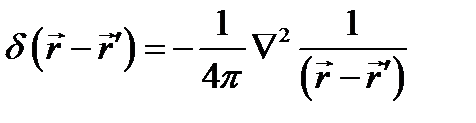 (8.14а)
(8.14а)
Полученный результат ниже будет использован при интегрировании уравнения Пуассона.
Метод разделения переменных
11.1. Сущность метода. Разделение переменных в цилиндрических координатах. При решении граничных задач для различных уравнений с частными производными широко используется так называемый метод разделения переменных, позволяющий свести исходную задачу вообще к трем (а в двумерном случае к двум) задачам для обыкновенных дифференциальных уравнений. Этот метод применим при пользовании декартовой, цилиндрической, сферической и несколькими другими системами координат, когда граничная поверхность задачи может рассматриваться как координатная (или иногда совокупность координатных поверхностей). Позднее мы будем применять метод разделения переменных к различным задачам электродинамики, а в данной главе он используется при решении граничных задач для уравнения Лапласа.
Поясним сущность метода разделения переменных на следующем примере. Пусть требуется найти решение граничной задачи для уравнения Лапласа (задачи Дирихле или Неймана, внутренней или внешней) для цилиндрической области при условии, что решение не зависит от продольной координаты z, т. е. неизменно вдоль оси цилиндра. Ввиду этого задача является двумерной: решение ищется как функция координат в плоскости поперечного сечении цилиндра. Согласно (6.17) уравнение Лапласа принимает вид:
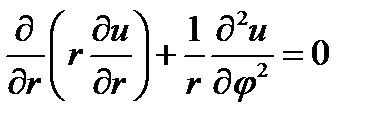 (11.1)
(11.1)
Предположим, что искомое решение 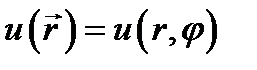 представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной:
представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной:
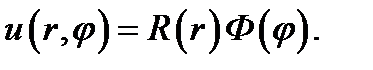 (11.2)
(11.2)
Мы увидим в дальнейшем, что это предположение оправдывается. Подстановка выражения (11.2) в уравнение Лапласа (11.1) с последующим умножением обоих слагаемых на r/RФ дает:
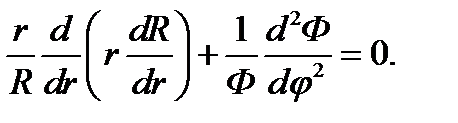 (11.3)
(11.3)
Таким образом, путём довольно простых операций удалось представить левую часть уравнения в виде суммы функций независимых аргументов: первое слагаемое в (11.3) зависит только от r, а второе - от φ. Простые рассуждения показывают, что эти слагаемые - константы. Действительно, фиксируя некоторое значение r и делая тем самым заведомо постоянным первое слагаемое, будем менять в возможных пределах φ, на что мы имеем право в силу независимости обоих слагаемых. Второе слагаемое, как видно из (11.3), остается при этом постоянным и равным первому с обратным знаком. Точно так же можно зафиксировать φ и убедиться, что первое слагаемое постоянно при изменении r. Постоянная величина, которой равно первое слагаемое, пока неизвестна; обозначим ее п2 и назовем постоянной разделения. Приравнивая слагаемые (11.3) постоянным п2 и - п2 соответственно, получаем после очевидных преобразований следующие два обыкновенных дифференциальных уравнения:
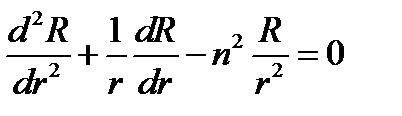 (11.4)
(11.4)
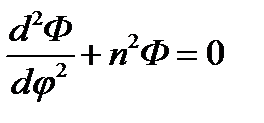
Это и есть результат «разделения переменных».
Теперь ясно, что решение уравнения Лапласа (11.1) в форме (11.2) существует, поскольку R и Ф есть решения обыкновенных дифференциальных уравнений (11.4). Найдём решения этих уравнений.
Начнем с более простого уравнения, стоящего во второй строке (11.4) и уже встречавшегося в п.7. Используя первую форму записи (7.8), выразим его общее решение в виде:
Ф = A cos nφ + В sin nφ, (11.5)
где А и В - произвольные постоянные. Поскольку функция Ф должна иметь период 2π, т. е.
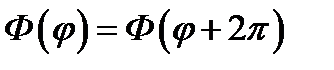 (11.6)
(11.6)
(возвращение в прежнюю точку после обхода), то
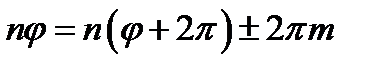 ,
,
где т - целое число или нуль. Отсюда следует, что
n=0, ± 1, ± 2,..., (11.7)
т. е. дробные значения п исключены. Ввиду неопределенности А и В,в (11.7) достаточно оставить положительные числа и нуль. В частности, при п = 0 из (11.5) находим, что Ф = А = const. Заметим, что при п = 0 уравнение во второй строчке (11.4) имеет и более общее непериодическое решение
W = Aφ + B,
которое ввиду (11.6) не является решением нашей задачи.
Уравнение в первой строчке (11.4) имеет общее решение
U = 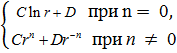 (11.8)
(11.8)
где С и D - произвольные постоянные.
Итак, решение уравнения Лапласа (11.1) представлено в виде произведения функций (11.2), определяемых формулами (11.5) и (11.8).
Значения произвольных констант, входящих в полученные решения, определяются, естественно, конкретными граничными условиями задачи.
Первая граничная задача
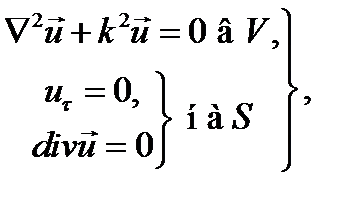 (18.41)
(18.41)
Вторая граничная задача
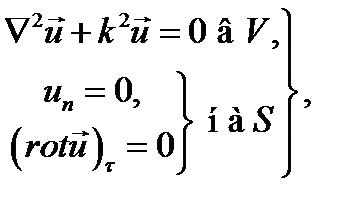 (18-42)
(18-42)
Сведения из алгебры
20.1. Векторы и матрицы. Запишем п линейных уравнений с п неизвестными:
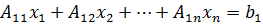
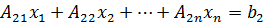 (20.1)
(20.1)
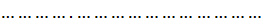
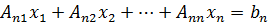
Существует ещё следующая краткая форма записи этой системы
Ах = B, (20.2)
где объект А, представляющий собой таблицу коэффициентов
A 11 A 12......... A 1n
A 21 A 22......... A 2n = А, (20.2а)
…………………..
A n



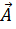 можно представить как
можно представить как 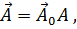 где
где 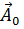 - единичный вектор (орт), а A - абсолютное значение вектора
- единичный вектор (орт), а A - абсолютное значение вектора 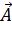 . Орты, соответствующие направлениям осей декартовой системы координат, будем обозначать
. Орты, соответствующие направлениям осей декартовой системы координат, будем обозначать 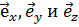 . Таким образом, в проекциях на эти оси вектор
. Таким образом, в проекциях на эти оси вектор 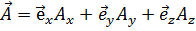 . (1.1)
. (1.1)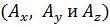 называются также его компонентами, или составляющими вектора.
называются также его компонентами, или составляющими вектора.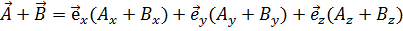 . (1.2)
. (1.2)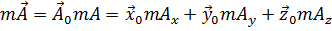 (1.3)
(1.3) обозначается
обозначается  и определяется следующим образом:
и определяется следующим образом: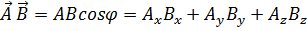 , (1.4)
, (1.4)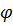 - угол между направлениями векторов. В результате скалярного произведения векторов образуется число. Как видно из (1.4), значение скалярного произведения может быть равным нулю при равных нулю исходных векторах
- угол между направлениями векторов. В результате скалярного произведения векторов образуется число. Как видно из (1.4), значение скалярного произведения может быть равным нулю при равных нулю исходных векторах 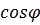 . В последнем случае эти векторы называются ортогональными: они направлены под прямым углом друг к другу.
. В последнем случае эти векторы называются ортогональными: они направлены под прямым углом друг к другу.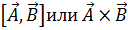 есть
есть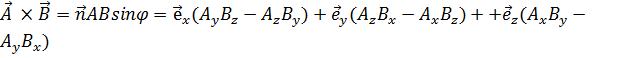 , (1.5)
, (1.5)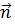 - единичный вектор, направленный по нормали к плоскости векторов
- единичный вектор, направленный по нормали к плоскости векторов 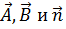 образуют «правую тройку» векторов: если смотреть вдоль
образуют «правую тройку» векторов: если смотреть вдоль 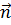 , то кратчайшее угловое расстояние между векторами
, то кратчайшее угловое расстояние между векторами 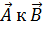 по часовой стрелке. Удобно записывать векторное произведение в форме следующего определителя:
по часовой стрелке. Удобно записывать векторное произведение в форме следующего определителя: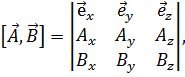 (1.5a)
(1.5a)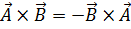 .(1.6)
.(1.6) понимается скаляр
понимается скаляр 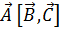 ; при этом
; при этом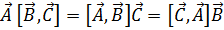 , (1.7).
, (1.7). , при сохранении которого безразлично, какие два вектора из трёх образуют векторное произведение. На основании (1.4) и (1.5) легко установить, что
, при сохранении которого безразлично, какие два вектора из трёх образуют векторное произведение. На основании (1.4) и (1.5) легко установить, что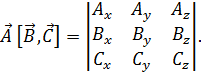 (1.8)
(1.8)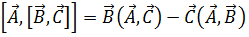 (1.9)
(1.9)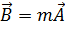 (1.10)
(1.10)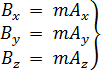 , (1.10а)
, (1.10а)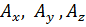 в аналогичный набор
в аналогичный набор 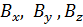 ; заметим, что эти совокупности компонент, вполне определяющие векторы
; заметим, что эти совокупности компонент, вполне определяющие векторы 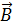 , компоненты которого определяются по формулам:
, компоненты которого определяются по формулам: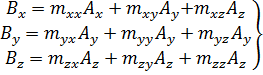 , (1.11)
, (1.11)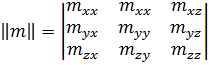 (1.12)
(1.12)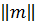 на вектор-столбец (
на вектор-столбец (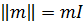 , где
, где (1.13)
(1.13)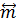 и запишем равенства (1.11) в следующей сокращённой форме:
и запишем равенства (1.11) в следующей сокращённой форме: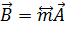 (1.14)
(1.14)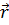 ,
,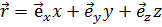 , (1.15)
, (1.15)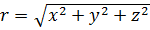 . (1.15а)
. (1.15а)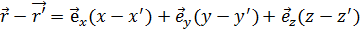 . (1.16)
. (1.16)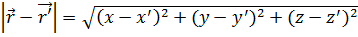 (1.16a)
(1.16a)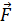 по некоторому контуру L не должна обязательно быть равной нулю. Подобно потоку вектора, циркуляция также может быть использована для локальной характеристики поля. При этом возникает понятие ротора вектора
по некоторому контуру L не должна обязательно быть равной нулю. Подобно потоку вектора, циркуляция также может быть использована для локальной характеристики поля. При этом возникает понятие ротора вектора 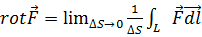 (4.1)
(4.1)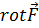 на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)
на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)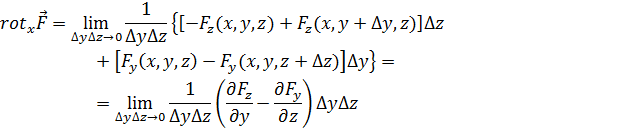
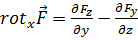 (4.2a)
(4.2a)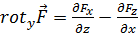 , (4.2б)
, (4.2б)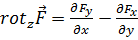 . (4.2в)
. (4.2в)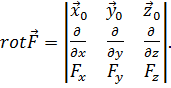 (4.3)
(4.3)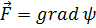 будет
будет 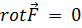 . Чтобы проверить тождество
. Чтобы проверить тождество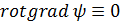 , (4.4)
, (4.4)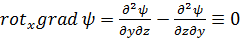 .
.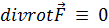 . (4.5)
. (4.5)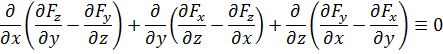
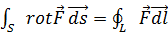 , (4.6)
, (4.6)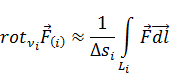
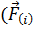 есть
есть 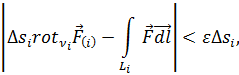

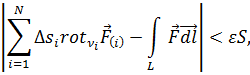
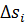 взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.
взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.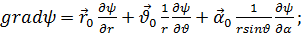 (6.18)
(6.18)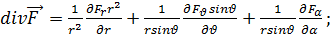 (6.19)
(6.19)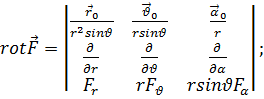 (6.20)
(6.20)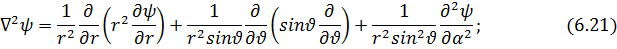
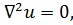 (7.1)
(7.1)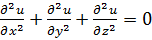 (7.2)
(7.2)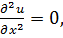 (7.3)
(7.3)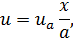
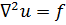 (7.5)
(7.5)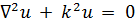 (7.6)
(7.6)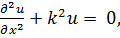 (7.7)
(7.7)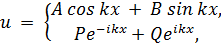 (7.8)
(7.8)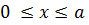 с условиями:
с условиями: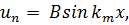
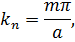
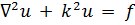 (7.10)
(7.10)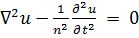 (7.11)
(7.11)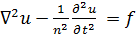 , (7.12)
, (7.12)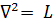 , в (7.6) и (7.10)
, в (7.6) и (7.10) 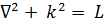 ив (7.11) и (7.12)
ив (7.11) и (7.12) 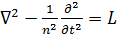 , запишем следующие легко проверяемые равенства:
, запишем следующие легко проверяемые равенства: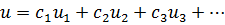
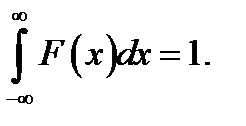 (8.1)
(8.1)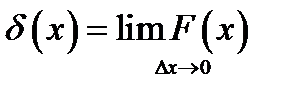 (8.2)
(8.2)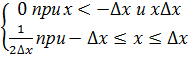 (8.3)
(8.3)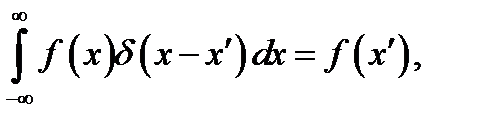 (8.4)
(8.4)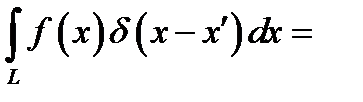
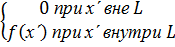 (8.5)
(8.5)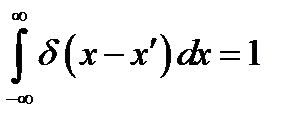 (8.4а)
(8.4а)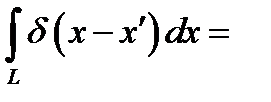
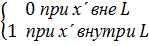 (8.5а)
(8.5а)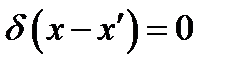 везде кроме точки
везде кроме точки 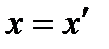 при сохранении интеграла (8.1). Это отвечает соотношениям (8.4 а), (8.5 а). Что касается формул (8.4) и (8.5), то всю область интегрирования, когда она включает точку х΄ можно заменить отрезком ΔL, покрывающим х' и настолько малым, что функцию f(x) на нем можно считать постоянной и равной f(x'). Поэтому
при сохранении интеграла (8.1). Это отвечает соотношениям (8.4 а), (8.5 а). Что касается формул (8.4) и (8.5), то всю область интегрирования, когда она включает точку х΄ можно заменить отрезком ΔL, покрывающим х' и настолько малым, что функцию f(x) на нем можно считать постоянной и равной f(x'). Поэтому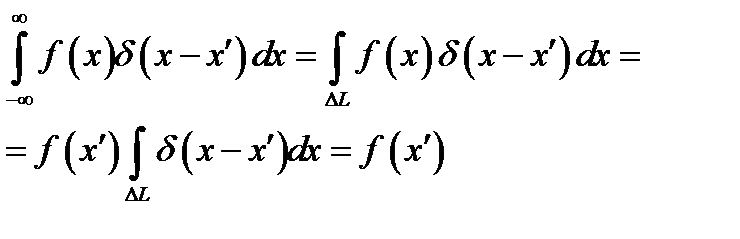 .
.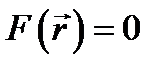 при
при 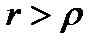
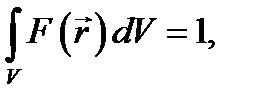
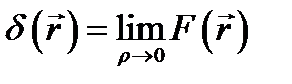
 , вместо (8.4) и (8.5) будем иметь:
, вместо (8.4) и (8.5) будем иметь: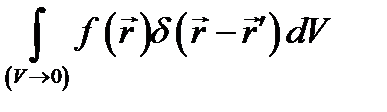 (8.6)
(8.6)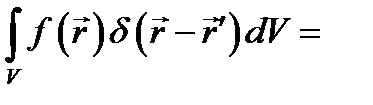
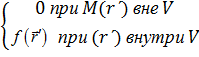 (8.7)
(8.7)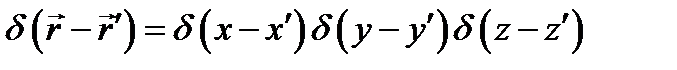 , (8.8)
, (8.8)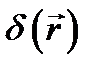 охарактеризуем плотность заряда
охарактеризуем плотность заряда 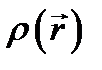 в пространстве при наличии точечного заряда q, расположенного в точке М
в пространстве при наличии точечного заряда q, расположенного в точке М 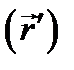 . Легко видеть, что
. Легко видеть, что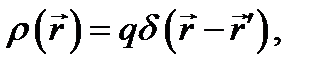 (8.9)
(8.9)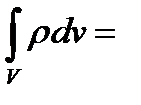
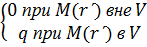 (8.10)
(8.10)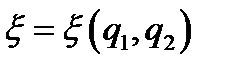 , его можно рассматривать как распределённый в объёме с плотностью
, его можно рассматривать как распределённый в объёме с плотностью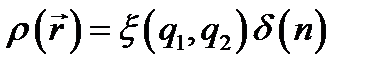 (8.11)
(8.11)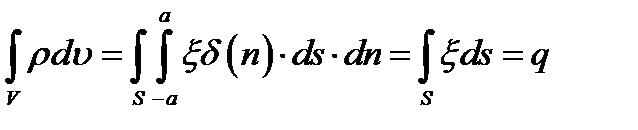
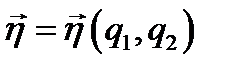 . Вместо
. Вместо 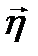 можно ввести плотность тока в объёме
можно ввести плотность тока в объёме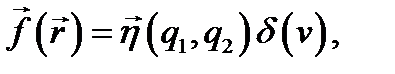 (8.12)
(8.12)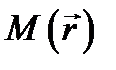 находятся на какой-либо поверхности S, пересекающей Р по линии l, a n - координатная линия в S.
находятся на какой-либо поверхности S, пересекающей Р по линии l, a n - координатная линия в S.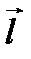 поверхностный ток описывается как ток в объёме с плотностью
поверхностный ток описывается как ток в объёме с плотностью 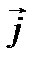 , проходящей через S:
, проходящей через S: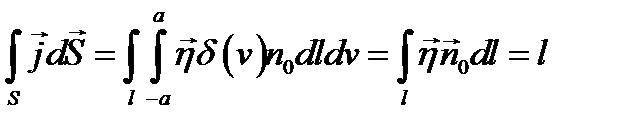
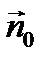 - орт нормали к l, касательный Р).
- орт нормали к l, касательный Р).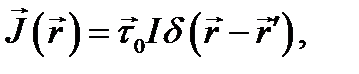 (8.13)
(8.13)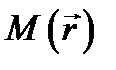 -и
-и 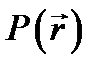 (последняя лежит на L)при интегрировании остаются на какой-либо поверхности, пересекаемой током. Вычисляя ток I, имеем:
(последняя лежит на L)при интегрировании остаются на какой-либо поверхности, пересекаемой током. Вычисляя ток I, имеем: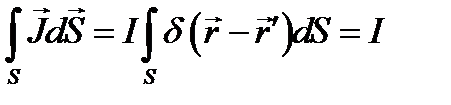
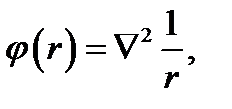
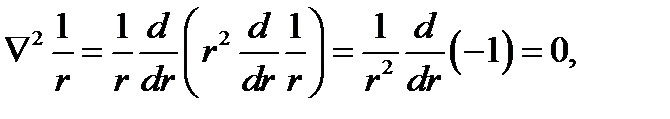
 по области V, содержащей начало координат r = 0; при помощи теоремы Остроградского-Гаусса преобразуем его к поверхностному:
по области V, содержащей начало координат r = 0; при помощи теоремы Остроградского-Гаусса преобразуем его к поверхностному: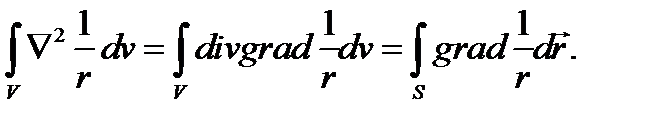
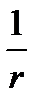 постоянна и согласно (6.18) или (2.12а) равна:
постоянна и согласно (6.18) или (2.12а) равна: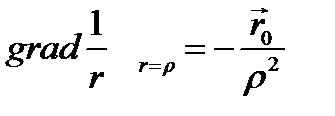
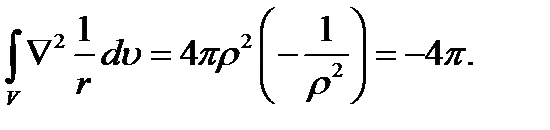
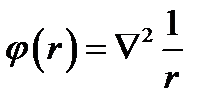 , равная нулю везде, кроме начала координат, при интегрировании по любой области, включающей начало, даёт - 4π. Поэтому, будучи умножена на -1/4π, эта функция удовлетворяет определению (8.6), (8.7). Это значит, что найдена дельта-функция
, равная нулю везде, кроме начала координат, при интегрировании по любой области, включающей начало, даёт - 4π. Поэтому, будучи умножена на -1/4π, эта функция удовлетворяет определению (8.6), (8.7). Это значит, что найдена дельта-функция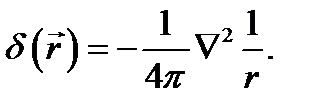 (8.14)
(8.14)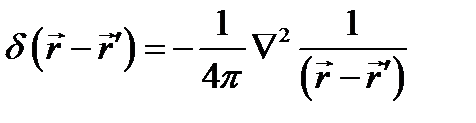 (8.14а)
(8.14а)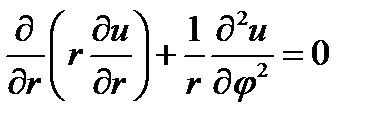 (11.1)
(11.1)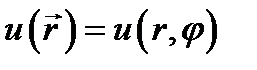 представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной:
представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной: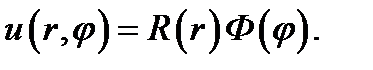 (11.2)
(11.2)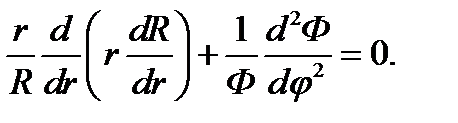 (11.3)
(11.3)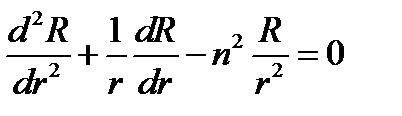 (11.4)
(11.4)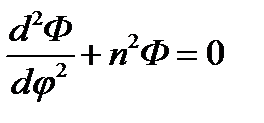
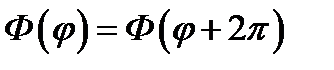 (11.6)
(11.6)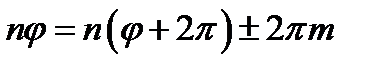 ,
,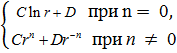 (11.8)
(11.8)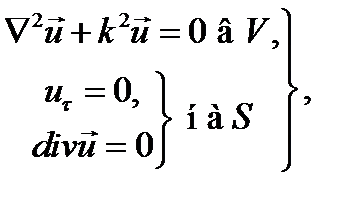 (18.41)
(18.41)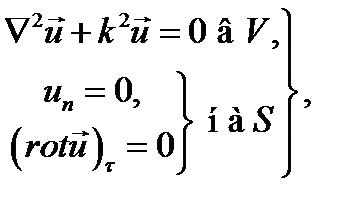 (18-42)
(18-42)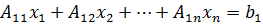
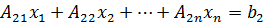 (20.1)
(20.1)