9.1. Функция Грина.Запишем уравнение Пуассона (7.5), обозначая неизвестную функцию и(r), а функцию, заданную в правой части,  :
:
 (9.1)
(9.1)
Как видно теперь, результат (8.14 а) можно истолковать в том смысле, что существует частная форма уравнении Пуассона
 (9.2)
(9.2)
имеющая решение:
 (9.3)
(9.3)
Последнее называют функцией Грина для уравнения Пуассона. Поскольку точку М (r')можно рассматривать в качестве переменной, то  является функцией аргументов r и r΄, относительно которых она симметрична, т. е.
является функцией аргументов r и r΄, относительно которых она симметрична, т. е.
 (9.4)
(9.4)
что непосредственно видно из (9.3).
Отметим, что полученная функция Грина (9.3) не является единственным решением уравнения (9.2). Действительно, вместо (9.3) можно записать решение, в виде:
 (9.5)
(9.5)
где  - любое решение уравнения Лапласа (7.1), т. е. уравнения (9.1). при f(r) = 0. Для сохранения свойства (9.4)
- любое решение уравнения Лапласа (7.1), т. е. уравнения (9.1). при f(r) = 0. Для сохранения свойства (9.4)  взято симметричным относительно
взято симметричным относительно 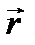 и
и 
9.2. Выражение решения скалярного уравнения Пуассона. Будем теперь искать некоторый общий вид решения уравнения Пуассона (9.1). С этой целью умножим (9.1) на G(r, r') и (9.2) - на и  , произведем вычитание левых и правых частей и интегрирование полученных выражений как функций
, произведем вычитание левых и правых частей и интегрирование полученных выражений как функций  по V, в результате чего получим:
по V, в результате чего получим:


Выполним здесь следующие преобразования:
а) объемный интеграл в левой части заменим поверхностным при помощи второй формулы Грина (5.14);
б) во втором слагаемом справа произведем интегрирование по формуле (8.7);
в) после этого поменяем местами обозначения  и
и 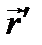 (ввиду равенства (9.4) данная операция на функцию Грина не распространяется); в знак того, что
(ввиду равенства (9.4) данная операция на функцию Грина не распространяется); в знак того, что  означает теперь переменную интегрирования, будем писать dv΄, ds' и v вместо dv, ds и v.
означает теперь переменную интегрирования, будем писать dv΄, ds' и v вместо dv, ds и v.
Указанные действия дают основание для записи:
 (9.6)
(9.6)
где S - поверхность, ограничивающая рассматриваемую область V. Это и есть общее интегральное представление решение  уравнения Пуассона (9.1). Как показывает формула (9.6), для того, чтобы найти решение
уравнения Пуассона (9.1). Как показывает формула (9.6), для того, чтобы найти решение  в V при заданной правой части
в V при заданной правой части 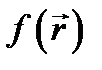 , надо ещё располагать информацией о поведении решения на границе S области V.
, надо ещё располагать информацией о поведении решения на границе S области V.
Внося в (9.6) выражение функции Грина (9.3), получаем более конкретную модификацию интегрального представления решения:
 (9.7)
(9.7)
9.3. Решение уравнения Пуассона для неограниченного пространства.Формулы (9.6) и (9.7) справедливы независимо от того, существует ли решение  только в области V с границей S, или V произвольным образом выделена внутри более широкой области, в которой определено решение.
только в области V с границей S, или V произвольным образом выделена внутри более широкой области, в которой определено решение.
Пусть решение и(r) определено во всём неограниченном пространстве, а функция  отлична от нуля только внутри некоторой ограниченной области. Тогда в (9.7) можно распространить интегрирование на всё пространство, отнеся границу S в бесконечность, однако под V для первого члена справа, в сущности, надо понимать лишь ту область, где
отлична от нуля только внутри некоторой ограниченной области. Тогда в (9.7) можно распространить интегрирование на всё пространство, отнеся границу S в бесконечность, однако под V для первого члена справа, в сущности, надо понимать лишь ту область, где  .Наиболее интересен класс задач для которых решение
.Наиболее интересен класс задач для которых решение  при r →∞ убывает не медленнее, чем 1/ r (как говорят, «регулярно в бесконечности»); при этом отношение
при r →∞ убывает не медленнее, чем 1/ r (как говорят, «регулярно в бесконечности»); при этом отношение 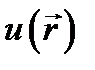 к 1/r при r →∞ остается ограниченным, что обозначается символом
к 1/r при r →∞ остается ограниченным, что обозначается символом  . Относя границу S в бесконечность, будем представлять её как сферическую поверхность неограниченно возрастающего радиуса r' с центром в начале координат.
. Относя границу S в бесконечность, будем представлять её как сферическую поверхность неограниченно возрастающего радиуса r' с центром в начале координат.
Тогда поверхностный интеграл в (9.7) принимает вид:

поскольку v ' = r΄. А так как для всякой фиксированной точки  будет
будет  и
и  , и кроме того
, и кроме того
 и
и  ,
,
то интегрируемая функция есть величина 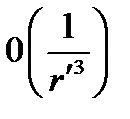 , в то время как дифференциал ds' пропорционален r'2. Это значит, что весь поверхностный интеграл, будучи величиной 0(1/ r '), при
, в то время как дифференциал ds' пропорционален r'2. Это значит, что весь поверхностный интеграл, будучи величиной 0(1/ r '), при  исчезает. Поэтому решение уравнения Пуассона в рассматриваемом случае дается формулой (9.7) при отбрасывании поверхностного интеграла:
исчезает. Поэтому решение уравнения Пуассона в рассматриваемом случае дается формулой (9.7) при отбрасывании поверхностного интеграла:
 (9.8)
(9.8)
Легко видеть, что решение, действительно, принадлежит требуемому классу, т. е.  .
.
9.4. Векторное уравнение Пуассона. Запишем векторное уравнение Пуассона
 (9.10)
(9.10)
и посмотрим, каким образом можно применить полученные выше результаты для нахождения его решения  в случае неограниченного пространства. Проецируя векторные функции на оси декартовой системы координат, получаем три скалярных уравнения Пуассона:
в случае неограниченного пространства. Проецируя векторные функции на оси декартовой системы координат, получаем три скалярных уравнения Пуассона:
 (9.10)
(9.10)
Если известно, что компоненты вектора  при r→∞ убывают не медленнее, чем 1/r, то каждая из них выражается формулой (9.8). Таким образом,
при r→∞ убывают не медленнее, чем 1/r, то каждая из них выражается формулой (9.8). Таким образом,

откуда получаем:
 (9.11)
(9.11)
что совпадает по форме с (9.8).



 :
: (9.1)
(9.1) (9.2)
(9.2) (9.3)
(9.3) является функцией аргументов r и r΄, относительно которых она симметрична, т. е.
является функцией аргументов r и r΄, относительно которых она симметрична, т. е. (9.4)
(9.4) (9.5)
(9.5) - любое решение уравнения Лапласа (7.1), т. е. уравнения (9.1). при f(r) = 0. Для сохранения свойства (9.4)
- любое решение уравнения Лапласа (7.1), т. е. уравнения (9.1). при f(r) = 0. Для сохранения свойства (9.4)  взято симметричным относительно
взято симметричным относительно 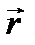 и
и 
 , произведем вычитание левых и правых частей и интегрирование полученных выражений как функций
, произведем вычитание левых и правых частей и интегрирование полученных выражений как функций  по V, в результате чего получим:
по V, в результате чего получим:

 и
и 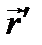 (ввиду равенства (9.4) данная операция на функцию Грина не распространяется); в знак того, что
(ввиду равенства (9.4) данная операция на функцию Грина не распространяется); в знак того, что  означает теперь переменную интегрирования, будем писать dv΄, ds' и v вместо dv, ds и v.
означает теперь переменную интегрирования, будем писать dv΄, ds' и v вместо dv, ds и v. (9.6)
(9.6) уравнения Пуассона (9.1). Как показывает формула (9.6), для того, чтобы найти решение
уравнения Пуассона (9.1). Как показывает формула (9.6), для того, чтобы найти решение  в V при заданной правой части
в V при заданной правой части 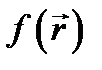 , надо ещё располагать информацией о поведении решения на границе S области V.
, надо ещё располагать информацией о поведении решения на границе S области V. (9.7)
(9.7) только в области V с границей S, или V произвольным образом выделена внутри более широкой области, в которой определено решение.
только в области V с границей S, или V произвольным образом выделена внутри более широкой области, в которой определено решение. отлична от нуля только внутри некоторой ограниченной области. Тогда в (9.7) можно распространить интегрирование на всё пространство, отнеся границу S в бесконечность, однако под V для первого члена справа, в сущности, надо понимать лишь ту область, где
отлична от нуля только внутри некоторой ограниченной области. Тогда в (9.7) можно распространить интегрирование на всё пространство, отнеся границу S в бесконечность, однако под V для первого члена справа, в сущности, надо понимать лишь ту область, где  .Наиболее интересен класс задач для которых решение
.Наиболее интересен класс задач для которых решение  при r →∞ убывает не медленнее, чем 1/ r (как говорят, «регулярно в бесконечности»); при этом отношение
при r →∞ убывает не медленнее, чем 1/ r (как говорят, «регулярно в бесконечности»); при этом отношение 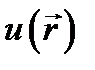 к 1/r при r →∞ остается ограниченным, что обозначается символом
к 1/r при r →∞ остается ограниченным, что обозначается символом  . Относя границу S в бесконечность, будем представлять её как сферическую поверхность неограниченно возрастающего радиуса r' с центром в начале координат.
. Относя границу S в бесконечность, будем представлять её как сферическую поверхность неограниченно возрастающего радиуса r' с центром в начале координат.
 будет
будет  и
и  , и кроме того
, и кроме того и
и  ,
,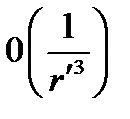 , в то время как дифференциал ds' пропорционален r'2. Это значит, что весь поверхностный интеграл, будучи величиной 0(1/ r '), при
, в то время как дифференциал ds' пропорционален r'2. Это значит, что весь поверхностный интеграл, будучи величиной 0(1/ r '), при  исчезает. Поэтому решение уравнения Пуассона в рассматриваемом случае дается формулой (9.7) при отбрасывании поверхностного интеграла:
исчезает. Поэтому решение уравнения Пуассона в рассматриваемом случае дается формулой (9.7) при отбрасывании поверхностного интеграла: (9.8)
(9.8) .
. (9.10)
(9.10) в случае неограниченного пространства. Проецируя векторные функции на оси декартовой системы координат, получаем три скалярных уравнения Пуассона:
в случае неограниченного пространства. Проецируя векторные функции на оси декартовой системы координат, получаем три скалярных уравнения Пуассона: (9.10)
(9.10) при r→∞ убывают не медленнее, чем 1/r, то каждая из них выражается формулой (9.8). Таким образом,
при r→∞ убывают не медленнее, чем 1/r, то каждая из них выражается формулой (9.8). Таким образом,
 (9.11)
(9.11)


