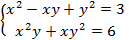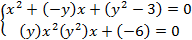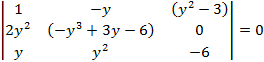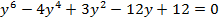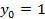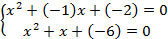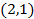Т: Любой симметрический многочлен 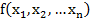 может быть представлен в виде многочлена от элементарных симметрических.
может быть представлен в виде многочлена от элементарных симметрических. 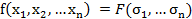
Доказательство:
Пусть f произвольный симметрический многочлен, если f =0 то F=0 если f≠0 то  он содержит лексикографически старший член s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/></w:rPr><m:t> </m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
он содержит лексикографически старший член s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/></w:rPr><m:t> </m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 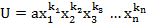 для которого выполняются условия лемм (1),(2). Составим разность
для которого выполняются условия лемм (1),(2). Составим разность  если
если 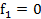 то
то 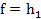 если
если  ≠0 то его лексикографически старший член
≠0 то его лексикографически старший член 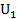 такой, что
такой, что 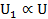 . Для члена
. Для члена 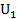 выполняются условия лемм (1),(2) а следовательно существует
выполняются условия лемм (1),(2) а следовательно существует  лексикографически старший член которого совпадает c
лексикографически старший член которого совпадает c 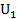 .
.
Рассмотрим разность:
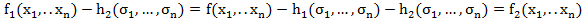
Если 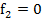 то
то 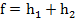
После конечного числа шагов построим многочлены  старшие члены которых удовлетворяют условию
старшие члены которых удовлетворяют условию  .Описанный процесс конечен потому что на конечном шаге получится нулевой, из этого соотношения следует, что показатели степеней переменной
.Описанный процесс конечен потому что на конечном шаге получится нулевой, из этого соотношения следует, что показатели степеней переменной 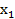 в одночленах U
в одночленах U 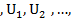 образуют не возрастающую последовательность так как все они не отрицательны то найдется такой номер
образуют не возрастающую последовательность так как все они не отрицательны то найдется такой номер 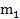 , что для всех
, что для всех  показатель степени переменной
показатель степени переменной 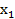 в одночлене
в одночлене 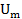 один и тоже и при лексикографическом сравнение показатель степени
один и тоже и при лексикографическом сравнение показатель степени 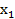 уже не будет играть роли и нужно сравнивать показатели переменной
уже не будет играть роли и нужно сравнивать показатели переменной 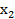 а показатели степеней
а показатели степеней  в этих одночленах также образуют не возрастающю последовательность и начиная с некоторого номера
в этих одночленах также образуют не возрастающю последовательность и начиная с некоторого номера 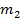 для всеех
для всеех 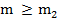 показатели
показатели 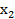 также будут равны между собой таким образом продолжая это рассуждение найдем такой номер
также будут равны между собой таким образом продолжая это рассуждение найдем такой номер 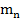 для
для 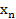 что для всех
что для всех 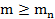 все соответствующее показатели одночленов равны и при этом условии лексикографически старший член
все соответствующее показатели одночленов равны и при этом условии лексикографически старший член 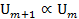 выразится не может, а это значит
выразится не может, а это значит 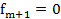 . По построению многочленов мы будем иметь
. По построению многочленов мы будем иметь 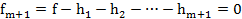
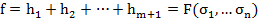 .
.

Пример 2:
Представить симметрический многочлен 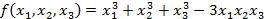 в виде многочлена
в виде многочлена 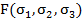 .
.
Лексикографически старший член многочлена f - 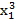 составим всевозможные наборы показателей
составим всевозможные наборы показателей 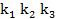 которые удовлетворяют следующим условиям
которые удовлетворяют следующим условиям
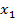
| 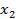
| 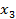
| f
| 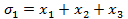
| 
| 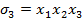
| F
|
| 1
| 1
| 1
| 0
| 3
| 3
| 1
| 27+3*3 a +1b
|
| 1
| 1
| 0
| 2
| 2
| 1
| 0
| 8+2a+0b
|

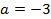

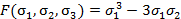
Проверка:
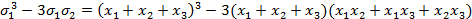
Теорема единственности
Л: пусть 
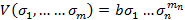
Если старшие члены U и V пропорциональны то соответствующие показатели степеней
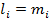 .
.
Доказательство:
Пусть лексикографически старший член U имеет вид 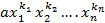 ,тогда по Л2
,тогда по Л2 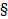 4
4 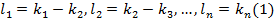 . Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами
. Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами 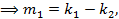 …,
…, 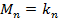 (на основании Т2
(на основании Т2 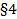 ), из (1),(2) ⟹
), из (1),(2) ⟹ 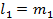 ….
…. 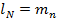 .
.
■
Т(Единственность): Всякий симметрический многочлен 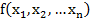 единственным образом представляется в виде многочлена от элементарных симметрических многочленов.
единственным образом представляется в виде многочлена от элементарных симметрических многочленов.
Доказательство:
Пусть для многочлена 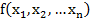 существует 2 различных многочлена
существует 2 различных многочлена 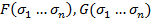
f 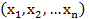 =F
=F 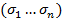
f 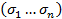 =G
=G 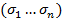
F≠G
Рассмотрим многочлен H 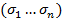 =F
=F 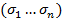 -G
-G 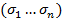 H
H 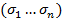 ≠0
≠0
Пусть  все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 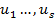 -старшие члены
-старшие члены  соответственно, среди них ассоциированных не будет(на основании Л3). Выберем из t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
соответственно, среди них ассоциированных не будет(на основании Л3). Выберем из t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 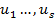 лексикографически старший пусть например им будет
лексикографически старший пусть например им будет  . После приведения подобных членов в сумме
. После приведения подобных членов в сумме  если
если  сохранится то эта сумма равна нулю быть не может, таким образом c одной стороны H равен 0 а, с другой стороны не равен, пришли к противоречию.
сохранится то эта сумма равна нулю быть не может, таким образом c одной стороны H равен 0 а, с другой стороны не равен, пришли к противоречию.
■
Дополнение к теме НОД). Результант 2 многочленов
Алгоритм Евклида позволяет найти НОД и НОК двух многочленов и в частности выяснить являются ли они взаимно простыми. Однако в явном виде алгоритм Евклида не дает условия которому должны удовлетворять коэффициенты 2 многочленов чтобы они были(не были) взаимно простыми. Поставим задачу найти соотношение между коэффициентами 2 многочленов выполнение которого было необходимо и достаточно, что бы многочлены не были взаимно простыми.
Пусть 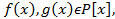
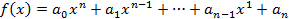
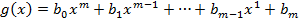
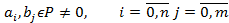
Найдем 
Если они взаимно простыми то их НОД= 1и 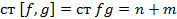 . Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда
. Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда
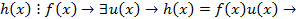

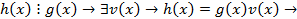
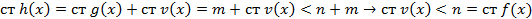
f g не являются взаимно простыми → существуют многочлен 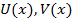 что,
что, 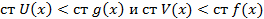 . Выясним когда такие многочлены существуют. Запишем многочлены:
. Выясним когда такие многочлены существуют. Запишем многочлены:
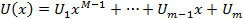
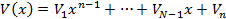
Подставим многочлены в равенство  получим:
получим:
s w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 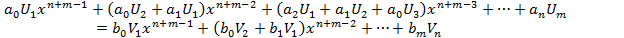
На основании определения равенства многочленов приравниваем их соответствующие коэффициенты(таких равенств будет m+n).
| Эта система имеет не нулевое решение если определитель равен 0. Для удобства умножим на -1 и транспонируем и его. Этот определитель называют результантом 2 многочленов.
| 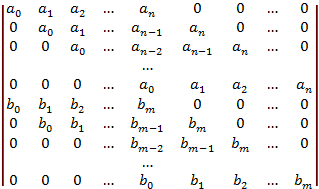
|
Т1: Многочлены f,g 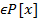 не являются взаимно простыми когда их результант равен 0.
не являются взаимно простыми когда их результант равен 0.
Результант 2 многочленов может быть применен не только для установления взаимной простоты многочленов но и для решения других задач например для исключения переменной из системы 2 алгебраических уравнений с 2 неизвестными.
О) Системой из m алгебраических уровней с n переменными называется система:
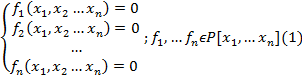
О) Системой 2 алгебраических уравнений с 2 неизвестными называют:
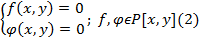
Запишем систему (2) в развернутом виде представив f и 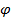 как многочлены от одной переменной x из кольца P[y]
как многочлены от одной переменной x из кольца P[y]
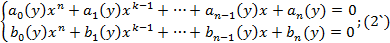
Положив 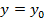 получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0:
получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0: 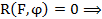
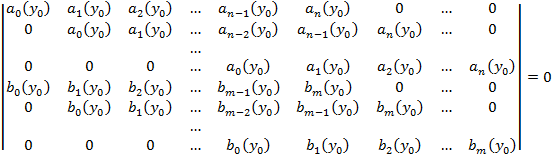
Подставив  в (2’), получаем решение
в (2’), получаем решение 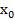 и общее решение
и общее решение 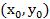 такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.
такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.
Пример 1:
Исключить переменную x и найти решение:
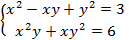
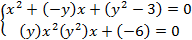


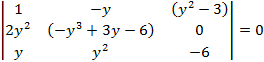
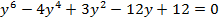
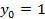
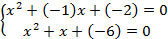

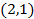
Т3:Многочлены над полем комплексных чисел. Уравнения 3 и 4 степени.



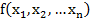 может быть представлен в виде многочлена от элементарных симметрических.
может быть представлен в виде многочлена от элементарных симметрических. 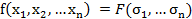
 он содержит лексикографически старший член s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/></w:rPr><m:t> </m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
он содержит лексикографически старший член s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/></w:rPr><m:t> </m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 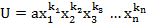 для которого выполняются условия лемм (1),(2). Составим разность
для которого выполняются условия лемм (1),(2). Составим разность  если
если 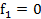 то
то 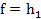 если
если  ≠0 то его лексикографически старший член
≠0 то его лексикографически старший член 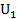 такой, что
такой, что 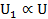 . Для члена
. Для члена  лексикографически старший член которого совпадает c
лексикографически старший член которого совпадает c 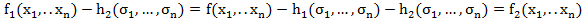
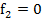 то
то 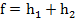
 старшие члены которых удовлетворяют условию
старшие члены которых удовлетворяют условию  .Описанный процесс конечен потому что на конечном шаге получится нулевой, из этого соотношения следует, что показатели степеней переменной
.Описанный процесс конечен потому что на конечном шаге получится нулевой, из этого соотношения следует, что показатели степеней переменной 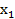 в одночленах U
в одночленах U 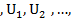 образуют не возрастающую последовательность так как все они не отрицательны то найдется такой номер
образуют не возрастающую последовательность так как все они не отрицательны то найдется такой номер 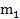 , что для всех
, что для всех  показатель степени переменной
показатель степени переменной 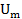 один и тоже и при лексикографическом сравнение показатель степени
один и тоже и при лексикографическом сравнение показатель степени 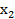 а показатели степеней
а показатели степеней  в этих одночленах также образуют не возрастающю последовательность и начиная с некоторого номера
в этих одночленах также образуют не возрастающю последовательность и начиная с некоторого номера 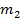 для всеех
для всеех 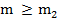 показатели
показатели 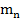 для
для 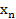 что для всех
что для всех 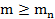 все соответствующее показатели одночленов равны и при этом условии лексикографически старший член
все соответствующее показатели одночленов равны и при этом условии лексикографически старший член 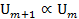 выразится не может, а это значит
выразится не может, а это значит 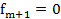 . По построению многочленов мы будем иметь
. По построению многочленов мы будем иметь 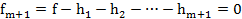
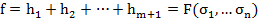 .
.
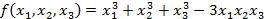 в виде многочлена
в виде многочлена 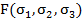 .
.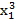 составим всевозможные наборы показателей
составим всевозможные наборы показателей 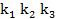 которые удовлетворяют следующим условиям
которые удовлетворяют следующим условиям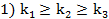 2)
2) 
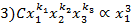

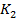
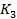
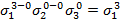
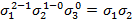
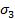
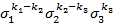
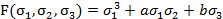
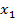
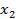
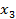
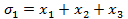

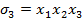

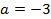

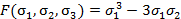
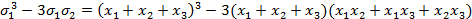

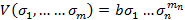
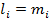 .
.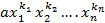 ,тогда по Л2
,тогда по Л2 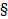 4
4  . Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами
. Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами 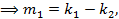 …,
…, 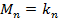 (на основании Т2
(на основании Т2 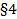 ), из (1),(2) ⟹
), из (1),(2) ⟹ 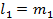 ….
…. 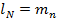 .
.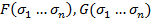
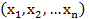 =F
=F 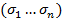
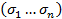 =G
=G  все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 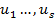 -старшие члены
-старшие члены  . После приведения подобных членов в сумме
. После приведения подобных членов в сумме  если
если 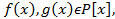
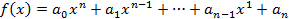
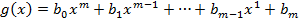
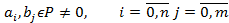

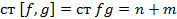 . Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда
. Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда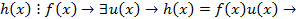

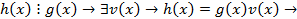
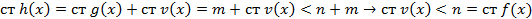
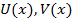 что,
что, 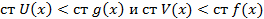 . Выясним когда такие многочлены существуют. Запишем многочлены:
. Выясним когда такие многочлены существуют. Запишем многочлены: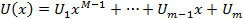
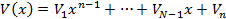
 получим:
получим: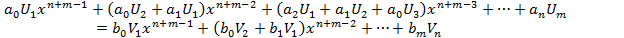
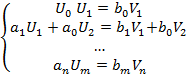
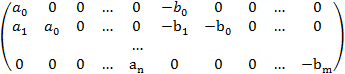
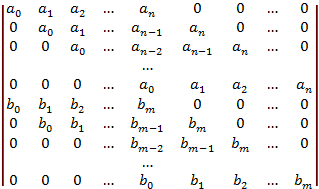
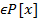 не являются взаимно простыми когда их результант равен 0.
не являются взаимно простыми когда их результант равен 0.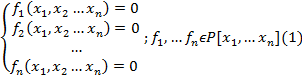
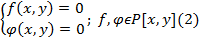
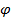 как многочлены от одной переменной x из кольца P[y]
как многочлены от одной переменной x из кольца P[y]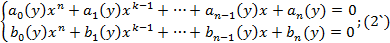
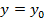 получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0:
получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0: 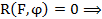
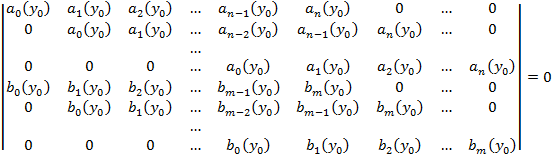
 в (2’), получаем решение
в (2’), получаем решение 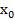 и общее решение
и общее решение 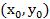 такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.
такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.