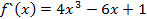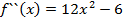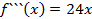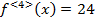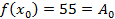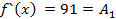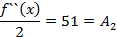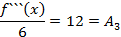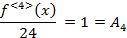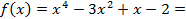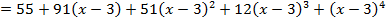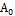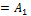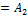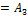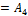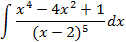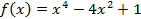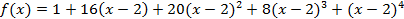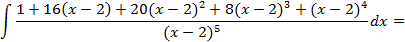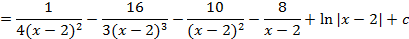В курсе математического анализа f(x) как функция действительной переменной имеет производную для любого 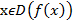 и производная является многочленом степень которого на единицу меньше f(x). Так производная понимается как конечный предел отношения приращения функции к приращению аргумента. Производную в алгебре определить так нельзя так как в абстрактном поле P над которым рассматривается многочлен в общем случае понятие придела лишено смысла. Например вопле вычетов понятие приращения аргумента не имеет смысла, по этому производную в алгебре понимают формально. Производной многочлена f(x) ∈P[x] называют многочлен
и производная является многочленом степень которого на единицу меньше f(x). Так производная понимается как конечный предел отношения приращения функции к приращению аргумента. Производную в алгебре определить так нельзя так как в абстрактном поле P над которым рассматривается многочлен в общем случае понятие придела лишено смысла. Например вопле вычетов понятие приращения аргумента не имеет смысла, по этому производную в алгебре понимают формально. Производной многочлена f(x) ∈P[x] называют многочлен 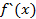 коофициенты которого являются кратными кофицеентам многочлена f(x). Производная многочлена 0 степени и нулевого многочлена принимается равной 0. Будем предполагать что, поле P имеет нулевую характеристику тогда для нахождения производных остаются справедливы правела дифференцирования рассмотренные в математическом анализе.
коофициенты которого являются кратными кофицеентам многочлена f(x). Производная многочлена 0 степени и нулевого многочлена принимается равной 0. Будем предполагать что, поле P имеет нулевую характеристику тогда для нахождения производных остаются справедливы правела дифференцирования рассмотренные в математическом анализе.
В случае конечной характеристики поля P указанные правила дифференцирования могут нарушатся.
Аналогично 1 производной можно определить 2 и другие формальные производные.
Не приводимые кратные множители многочлена.
О1) Не приводимый над полем P называется множитель кратности k≥1 многочлена f(x) если в каноническом разложении многочлен p(x) содержится в k степени.
Т: если неприводимый над полем P нулевой характеристики, многочлен p(x) в каноническом разложении f(x) над P входит в k степени, то в каноническое разложение формальной производной он входит в k-1 степени.
Доказательство:
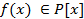
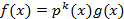
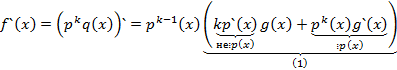
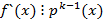
Теорема будет доказана если мы покажем что, (1) не делится на p(x). Второе слагаемое делится на p(x) а, первое слагаемое не делится на p(x) так как g(x)p(x) взаимно просты, 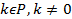 . P(x) не приводим, значит
. P(x) не приводим, значит 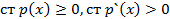 значит p(x) не нулевой таким образом в каноническом разложении
значит p(x) не нулевой таким образом в каноническом разложении 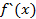
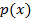 входит в k-1 степени.
входит в k-1 степени.
■
Замечание: Если не приводимый многочлен над полем P нулевой характеристики в каноническом разложении кольца P[x] содержится в первой степени то в каноническое разложение производной он не входит.
Доказательство:

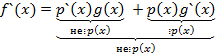
Значит в каноническое разложение p(x) войти не может.
■
Замечание: Чтобы многочлен f(x) не имел кратных множителей над полем P необходимо и достаточно чтобы f(x) и f`(x) были взаимно простыми.
Доказательство:
⟹ Пусть многочлен f(x) не содержит в каноническом разложении кратных множителей тогда по следствию (1) эти множители в каноническом разложении производной f`(x) отсутствуют то есть f(x) и f`(x) не имеют общих делителей кроме единице (f(x),f`(x))=1
⟸ Пусть (f(x),f`(x))=1. Рассуждая с помощью метода от противного, приходим к противоречию.
■
Кратные корни многочлена
О) Элемент 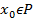 называется корнем k-ой кратности для многочлена
называется корнем k-ой кратности для многочлена 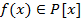 если
если 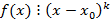 но не делится
но не делится 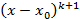 .
.
Пример 1:
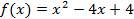
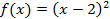
x=2 - корень 2 кратности.
Т1: Чтобы элемент 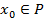 был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие
был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие 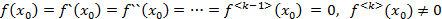 (1)
(1)
Доказательство:
⟹ Пусть 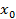 корень k-ой кратности для многочлена
корень k-ой кратности для многочлена 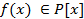 тогда по определению будим иметь
тогда по определению будим иметь 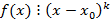 то есть
то есть 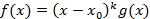 где
где 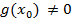 , учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени:
, учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени:
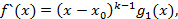 где
где 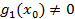 причем
причем 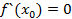 . Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
. Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 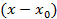 войдет в k-2 степени.
войдет в k-2 степени.
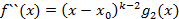 , где
, где 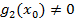 причем
причем 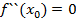 действуя так далее находим
действуя так далее находим 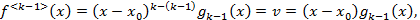 причем
причем
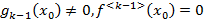
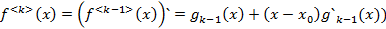 не
не 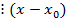 , т.е.
, т.е. 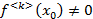 .
.
⟸ Пусть выполнены требования 1 то есть 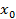 корень многочлена f(x) пусть кратность этого корня равна
корень многочлена f(x) пусть кратность этого корня равна 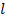 и она отличается от k:
и она отличается от k:
1) 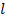 <k è
<k è 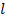 -1<k-1 è
-1<k-1 è 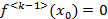
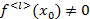 учитывая, что
учитывая, что 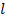 ≤k-1 (по доказанной первой части теоремы
≤k-1 (по доказанной первой части теоремы 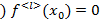 полученные соотношения противоречивы.
полученные соотношения противоречивы.
2) 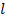 >k по первой части доказанной теоремы получится:
>k по первой части доказанной теоремы получится:
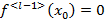
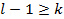
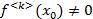
получили противоречивые соотношения таким образом 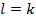 .
.
■
§14 разложение многочлена по степеням двучлена 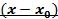
Пусть дан многочлен f(x) ∈P[x] с нулевой характеристикой и степень его равна n.
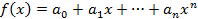
Поставим задачу разложить f (x) по степеням 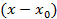 где
где 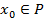 то есть представим многочлен f(x) в виде
то есть представим многочлен f(x) в виде 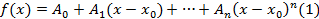 где
где 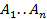 подлежат отысканию. Многочлен в виде (1) продифференцируем n раз:
подлежат отысканию. Многочлен в виде (1) продифференцируем n раз:
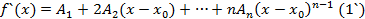
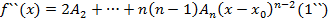
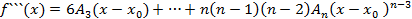

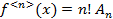
Подставляя в полученные неравенства 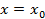 :
:
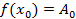
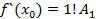
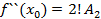
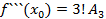

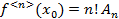
Подставим найденные коэффициенты в (1) получим:
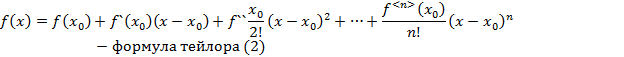
Коэффициенты в (2) определяются однозначно.
Пример 1:
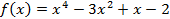 разложить по степеням
разложить по степеням 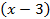 .
.
Пример 2:
Найти интеграл:
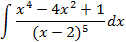
Т2: Многочлены от нескольких переменных.



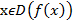 и производная является многочленом степень которого на единицу меньше f(x). Так производная понимается как конечный предел отношения приращения функции к приращению аргумента. Производную в алгебре определить так нельзя так как в абстрактном поле P над которым рассматривается многочлен в общем случае понятие придела лишено смысла. Например вопле вычетов понятие приращения аргумента не имеет смысла, по этому производную в алгебре понимают формально. Производной многочлена f(x) ∈P[x] называют многочлен
и производная является многочленом степень которого на единицу меньше f(x). Так производная понимается как конечный предел отношения приращения функции к приращению аргумента. Производную в алгебре определить так нельзя так как в абстрактном поле P над которым рассматривается многочлен в общем случае понятие придела лишено смысла. Например вопле вычетов понятие приращения аргумента не имеет смысла, по этому производную в алгебре понимают формально. Производной многочлена f(x) ∈P[x] называют многочлен 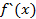 коофициенты которого являются кратными кофицеентам многочлена f(x). Производная многочлена 0 степени и нулевого многочлена принимается равной 0. Будем предполагать что, поле P имеет нулевую характеристику тогда для нахождения производных остаются справедливы правела дифференцирования рассмотренные в математическом анализе.
коофициенты которого являются кратными кофицеентам многочлена f(x). Производная многочлена 0 степени и нулевого многочлена принимается равной 0. Будем предполагать что, поле P имеет нулевую характеристику тогда для нахождения производных остаются справедливы правела дифференцирования рассмотренные в математическом анализе.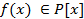
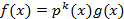
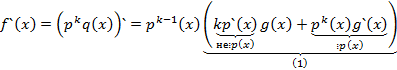
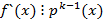
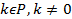 . P(x) не приводим, значит
. P(x) не приводим, значит 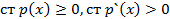 значит p(x) не нулевой таким образом в каноническом разложении
значит p(x) не нулевой таким образом в каноническом разложении 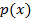 входит в k-1 степени.
входит в k-1 степени.
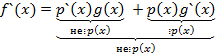
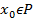 называется корнем k-ой кратности для многочлена
называется корнем k-ой кратности для многочлена 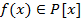 если
если 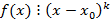 но не делится
но не делится 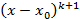 .
.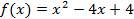
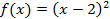
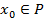 был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие
был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие 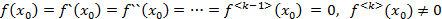 (1)
(1)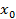 корень k-ой кратности для многочлена
корень k-ой кратности для многочлена 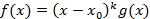 где
где 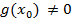 , учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени:
, учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени: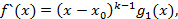 где
где 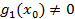 причем
причем 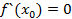 . Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
. Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 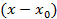 войдет в k-2 степени.
войдет в k-2 степени.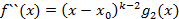 , где
, где 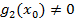 причем
причем 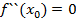 действуя так далее находим
действуя так далее находим 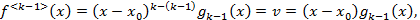 причем
причем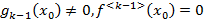
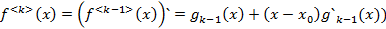 не
не 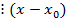 , т.е.
, т.е. 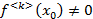 .
.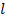 и она отличается от k:
и она отличается от k: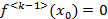
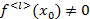 учитывая, что
учитывая, что 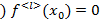 полученные соотношения противоречивы.
полученные соотношения противоречивы.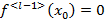
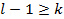
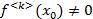
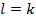 .
.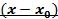
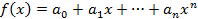
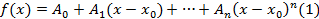 где
где 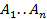 подлежат отысканию. Многочлен в виде (1) продифференцируем n раз:
подлежат отысканию. Многочлен в виде (1) продифференцируем n раз: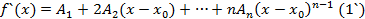
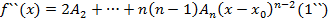
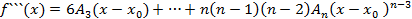

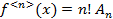
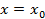 :
: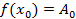
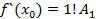
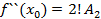
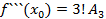
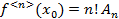
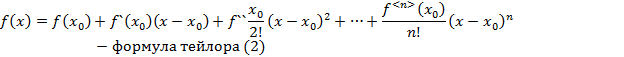
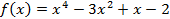 разложить по степеням
разложить по степеням 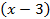 .
.