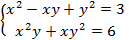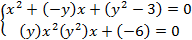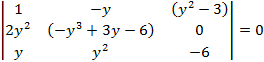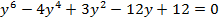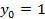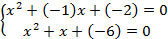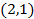Л1 02.09.09 Алгебра многочленов
Лит: Винбег Алгебра многочленов
Задачник практикум
Т1: Многочлены от одной переменной
Многочлены как функции действительной переменной
Рассмотри понятия многочлена или целой рациональной функции от одной переменной.
О1) функция вида:
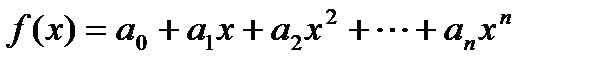 (1) –называется многочленом
(1) –называется многочленом
Где 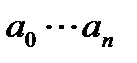 действительные числа, x действительная переменная, n целое число- степень многочлена.
действительные числа, x действительная переменная, n целое число- степень многочлена.
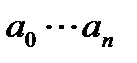 коэффициенты, Число n называют степенью многочлена,
коэффициенты, Число n называют степенью многочлена, 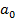 – свободный член.
– свободный член.
С точке зрения мат записи имеем сумму например:
 - 1 степени;
- 1 степени;
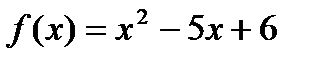 -2 степени;
-2 степени;
Частным случаем является постоянная функция f(x)=a,a-cost.
Многочлен коэффициенты которого равны 0 называется, многочлен нулевой степени.
Заметим что над многочленами можно выполнять: сложение, вычитание, умножения в результате чего получается снова многочлен. Пусть имеется многочлен (1) и многочлен:  ;(2)
;(2)
тогда:
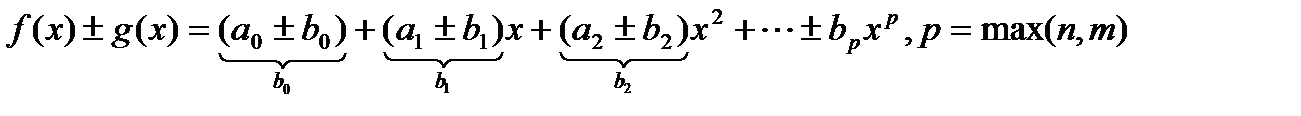 ;
;
Произведением многочленов f и g называется сумме всевозможных произведений U*V где U любой член из f(x), а V из g(x) тогда:
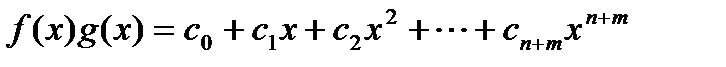 ;
;
где:
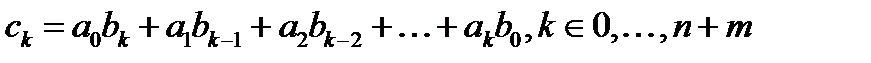
Так как сумма, разность и произведение многочленов также являются многочленом то многочлены образуют под кольцо в кольце всех функций действительного аргумента. Кольцо многочленов от действительной переменной x обозначается R[x]. Поскольку кольцо всех функций коммутативно и ассоциативно кольцо R[x] также обладает этими свойствами а значит в нем существует единичный элемент f(x)=1. Многочлены в алгебре также в связи с решением уравнений f(x)=0 где левая часть многочлен n-ной степени от одной переменной то в этом случае многочлен рассматривается как многочлен комплексной переменно. В алгебре рассматривают многочлены на более общих алгебраических системах, коэффициенты которых принадлежат произвольному кольцу, значительно отличаются от многочленов с числовыми коэффициентами.
Алгебраическое определение кольца многочленов
О1) Пусть R[x] произвольное кольцо многочленов от переменной х с коэффициентами из R назовем формальное выражение:
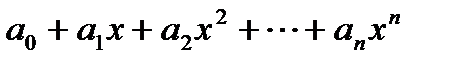 (1)
(1)
где n целое число выражение (1) надо рассматривать как единый символ у которого операции над отдельными частями не подразумевается 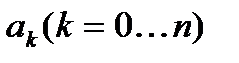 будем называть коэффициентами многочлена (1) при
будем называть коэффициентами многочлена (1) при  , а для всех k>n коэффициент при
, а для всех k>n коэффициент при 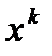 равен 0 для обозначения многочлена используют
равен 0 для обозначения многочлена используют 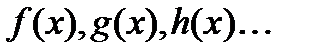 .
.
Два многочлена будем считать равными если каждый коэффициент 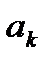 из
из 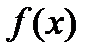 равен соответствующему коэффициенту
равен соответствующему коэффициенту 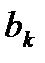 из
из 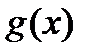 и записывается f(x)=g(x).
и записывается f(x)=g(x).
Для многочленов (1) и(2) определим их сумму f(x)+g(x) и произведение f(x)*g(x) по формулам рассмотренным в §1. Эти определения согласуются с данным выше определением равенства многочленов:
f1(x)=f2(x);
g1(x)=g2(x);
f1(x)+g1(x)=f2(x)+g2(x);
f1(x)*g1(x)=f2(x)*g2(x);
Деление с остатком
Между кольцом многочленов от одной переменной и кольцом целых чисел имеется глубокая аналогия проявляющаяся в свойствах делимости, в разложении на простые множества причина аналоги состоит в том что, в обоих этих кольца выполнимо деление с остатком благодаря чему оба эти кольца являются евклидовыми.
Т(Делении с остатком): Пусть P произвольное поле, P[x] кольцо многочленов с коэффициентами из P возьмем f(x) и g(x)≠0 тогда существует единственная пара многочлена q(x),r(x) ∈P[x] удовлетворяющая условиям:
1)f(x)=g(x)q(x)+z(x)
2)ст z(x)<ст g(x).
Доказательство:
Пусть:
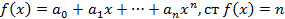
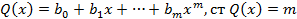
Если n<m то не полное частное равно 0 а, остаток совпадет с самим многочленом f(x).
Рассмотри когда n≥m. Построим многочлен 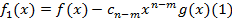 ,
, 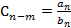
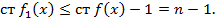 Обозначим
Обозначим 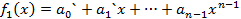 .
.
Аналогично построим 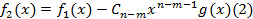 . Где
. Где 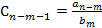 ,
, 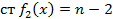 .
.
Продолжая процесс построения многочленов будет получена конечная последовательность многочленов и последний многочлен будет иметь номер n-m+1 и имеет степень 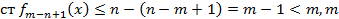 -степень многочлена g(x). Последний многочлен:
-степень многочлена g(x). Последний многочлен: 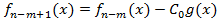 . Почвенное сложение равенств (1) (2) и т.д. дает возможность выразить многочлен f(x) через g(x):
. Почвенное сложение равенств (1) (2) и т.д. дает возможность выразить многочлен f(x) через g(x):
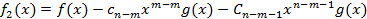
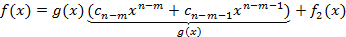
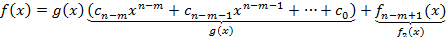
То есть наш многочлен представим в виде:
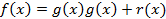
Докажем единственность такова представления методом от противного.
Предположим что, существуют такие многочлены 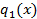 и
и 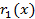 что, выполняется:
что, выполняется: 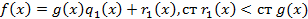 тогда:
тогда:
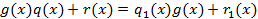
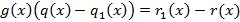
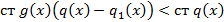
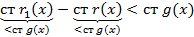
Учитывая что, степень левой части больше или равна а, степень правой ее не превосходит получили противоречие из которого следует: 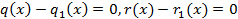
Рассмотренная процедура деления с остатком лежит в основе отыскания наибольшего делителя 2 многочленов.
Кратные корни многочлена
О) Элемент 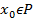 называется корнем k-ой кратности для многочлена
называется корнем k-ой кратности для многочлена 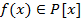 если
если 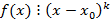 но не делится
но не делится 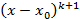 .
.
Пример 1:
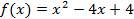
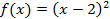
x=2 - корень 2 кратности.
Т1: Чтобы элемент 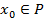 был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие
был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие 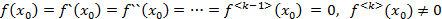 (1)
(1)
Доказательство:
⟹ Пусть 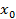 корень k-ой кратности для многочлена
корень k-ой кратности для многочлена 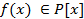 тогда по определению будим иметь
тогда по определению будим иметь 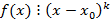 то есть
то есть 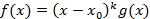 где
где 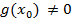 , учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени:
, учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени:
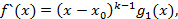 где
где 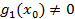 причем
причем 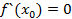 . Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
. Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 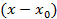 войдет в k-2 степени.
войдет в k-2 степени.
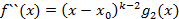 , где
, где 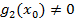 причем
причем 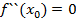 действуя так далее находим
действуя так далее находим 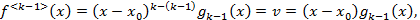 причем
причем
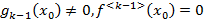
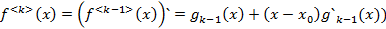 не
не 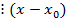 , т.е.
, т.е. 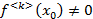 .
.
⟸ Пусть выполнены требования 1 то есть 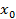 корень многочлена f(x) пусть кратность этого корня равна
корень многочлена f(x) пусть кратность этого корня равна 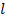 и она отличается от k:
и она отличается от k:
1) 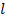 <k è
<k è 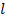 -1<k-1 è
-1<k-1 è 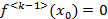
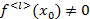 учитывая, что
учитывая, что 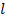 ≤k-1 (по доказанной первой части теоремы
≤k-1 (по доказанной первой части теоремы 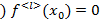 полученные соотношения противоречивы.
полученные соотношения противоречивы.
2) 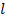 >k по первой части доказанной теоремы получится:
>k по первой части доказанной теоремы получится:
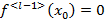
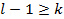
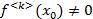
получили противоречивые соотношения таким образом 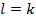 .
.
■
§14 разложение многочлена по степеням двучлена 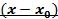
Пусть дан многочлен f(x) ∈P[x] с нулевой характеристикой и степень его равна n.
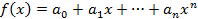
Поставим задачу разложить f (x) по степеням 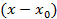 где
где 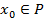 то есть представим многочлен f(x) в виде
то есть представим многочлен f(x) в виде 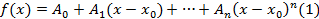 где
где 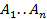 подлежат отысканию. Многочлен в виде (1) продифференцируем n раз:
подлежат отысканию. Многочлен в виде (1) продифференцируем n раз:
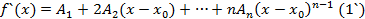
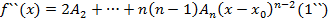
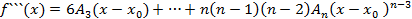

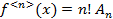
Подставляя в полученные неравенства 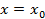 :
:
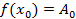
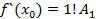
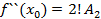
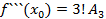

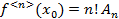
Подставим найденные коэффициенты в (1) получим:
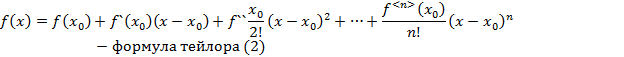
Коэффициенты в (2) определяются однозначно.
Пример 1:
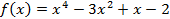 разложить по степеням
разложить по степеням 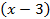 .
.
Пример 2:
Найти интеграл:
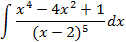
Т2: Многочлены от нескольких переменных.
Cсимметрические многочлены
Будим рассматривать многочлены над произвольной областью целостности.
О1 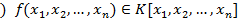 называется симметрическим если он не меняется при любой перестановке входящих в него переменных
называется симметрическим если он не меняется при любой перестановке входящих в него переменных 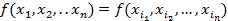 где
где  –перестановка
–перестановка
Пример 1:
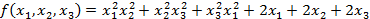 – симметрический
– симметрический
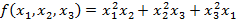 - не симметрический
- не симметрический
Структура симметрических многочленов такова, что если сам симметрический многочлен содержит элемент 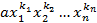 , то он также должен содержать многочлен вида
, то он также должен содержать многочлен вида 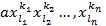 у которых выполнена замена иксов, а индексы образуют перестановку
у которых выполнена замена иксов, а индексы образуют перестановку  из номеров переменных x. Обозначим сумм различных одночленов, которые получаются из одночлена
из номеров переменных x. Обозначим сумм различных одночленов, которые получаются из одночлена 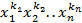 ,
, 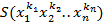 . В частности каждый симметрический многочлен является суммой однородных многочленов
. В частности каждый симметрический многочлен является суммой однородных многочленов

Особую роль среди симметрических многочленов играют элементарные симметрические многочлены.
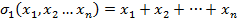
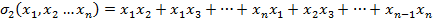
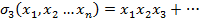
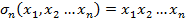
По определению k-ый элементарный симметрический многочлен есть сумм всевозможных произведений по k различных переменных
Другую важную серию симметрических многочленов составляют степенные суммы:
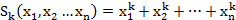
Можно показать что, сумма разность и произведение симметрических многочленов также являются симметрическими
Пример 2:
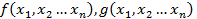 –симметрические
–симметрические 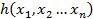 их произведение надо показать что он тоже симметрический
их произведение надо показать что он тоже симметрический
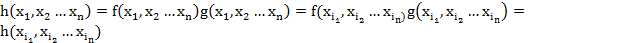 è
è 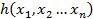 - симметрический.
- симметрический.
K 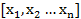 из него можем выделить симметрические. Сами симметрический многочлен тоже образуют кольцо.
из него можем выделить симметрические. Сами симметрический многочлен тоже образуют кольцо.
Рассмотрим ряд утверждений относительно симметрически многочленов.
Л1: Если 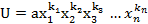 лексико старший член симметрического многочлена
лексико старший член симметрического многочлена  то для последовательности степеней
то для последовательности степеней 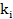 выполняется
выполняется 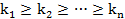 .
.
Доказательство:
Пусть u лексикографически старший член. Предположим  . По условию f симметрический тогда по определению симметрического многочлена он в месте с одночленом U содержит одночлен
. По условию f симметрический тогда по определению симметрического многочлена он в месте с одночленом U содержит одночлен 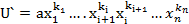 . Исходя из предположения
. Исходя из предположения 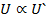 но по условию U старший то есть наше предположение привело к противоречию условию леммы следовательно наше предположение не верно.
но по условию U старший то есть наше предположение привело к противоречию условию леммы следовательно наше предположение не верно.

Л2: Для любого одночлена 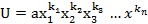 где
где 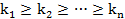 , a≠0 суш шествует многочлен
, a≠0 суш шествует многочлен 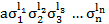 лексикографически старшй член которого совподает c U.
лексикографически старшй член которого совподает c U.
Доказательство:
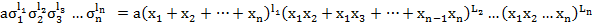
Лексикографически старший член многочлена 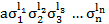 является произведением старших членов элементарных симметричных многочленов с учетом их степеней:
является произведением старших членов элементарных симметричных многочленов с учетом их степеней:
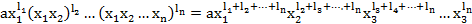
Найденный лексикографически старший член должен быть равен одночлену U если
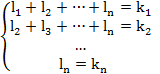 (2)
(2)
Решение системы (2) получаем в результате вычитания из i-го уравнения i+1 уравнение:
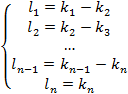 (3)
(3)
Такое решение единственно и учитывая что, 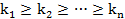 ,
, 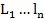 - целые не отрицательные числа а, следовательно могут быть показателями степеней. И так симметрический многочлен:
- целые не отрицательные числа а, следовательно могут быть показателями степеней. И так симметрический многочлен:
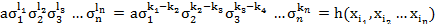
и лексикографически старший член ее совпадает с U(он единственен, что идет из единственности решения системы 2).

Доказанные леммы 1,2 позволяют рассмотреть основную теорему о симметрических многочленов.
Теорема единственности
Л: пусть 
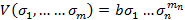
Если старшие члены U и V пропорциональны то соответствующие показатели степеней
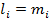 .
.
Доказательство:
Пусть лексикографически старший член U имеет вид 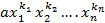 ,тогда по Л2
,тогда по Л2 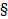 4
4 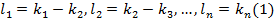 . Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами
. Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами 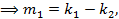 …,
…, 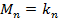 (на основании Т2
(на основании Т2 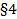 ), из (1),(2) ⟹
), из (1),(2) ⟹ 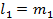 ….
…. 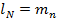 .
.
■
Т(Единственность): Всякий симметрический многочлен 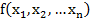 единственным образом представляется в виде многочлена от элементарных симметрических многочленов.
единственным образом представляется в виде многочлена от элементарных симметрических многочленов.
Доказательство:
Пусть для многочлена 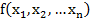 существует 2 различных многочлена
существует 2 различных многочлена 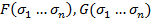
f 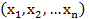 =F
=F 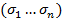
f 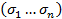 =G
=G 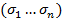
F≠G
Рассмотрим многочлен H 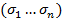 =F
=F 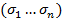 -G
-G 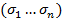 H
H 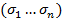 ≠0
≠0
Пусть  все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 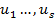 -старшие члены
-старшие члены  соответственно, среди них ассоциированных не будет(на основании Л3). Выберем из t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
соответственно, среди них ассоциированных не будет(на основании Л3). Выберем из t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 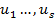 лексикографически старший пусть например им будет
лексикографически старший пусть например им будет  . После приведения подобных членов в сумме
. После приведения подобных членов в сумме  если
если  сохранится то эта сумма равна нулю быть не может, таким образом c одной стороны H равен 0 а, с другой стороны не равен, пришли к противоречию.
сохранится то эта сумма равна нулю быть не может, таким образом c одной стороны H равен 0 а, с другой стороны не равен, пришли к противоречию.
■
Дополнение к теме НОД). Результант 2 многочленов
Алгоритм Евклида позволяет найти НОД и НОК двух многочленов и в частности выяснить являются ли они взаимно простыми. Однако в явном виде алгоритм Евклида не дает условия которому должны удовлетворять коэффициенты 2 многочленов чтобы они были(не были) взаимно простыми. Поставим задачу найти соотношение между коэффициентами 2 многочленов выполнение которого было необходимо и достаточно, что бы многочлены не были взаимно простыми.
Пусть 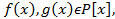
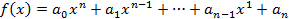
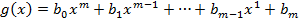
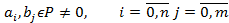
Найдем 
Если они взаимно простыми то их НОД= 1и 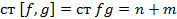 . Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда
. Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда
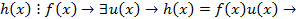

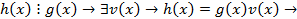
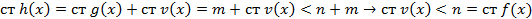
f g не являются взаимно простыми → существуют многочлен 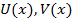 что,
что, 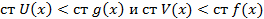 . Выясним когда такие многочлены существуют. Запишем многочлены:
. Выясним когда такие многочлены существуют. Запишем многочлены:
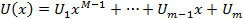
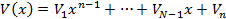
Подставим многочлены в равенство  получим:
получим:
s w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 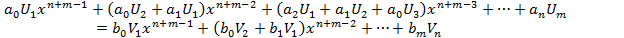
На основании определения равенства многочленов приравниваем их соответствующие коэффициенты(таких равенств будет m+n).
| Эта система имеет не нулевое решение если определитель равен 0. Для удобства умножим на -1 и транспонируем и его. Этот определитель называют результантом 2 многочленов.
| 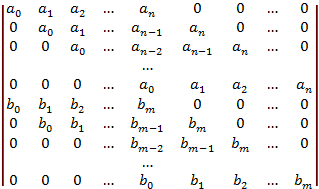
|
Т1: Многочлены f,g 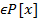 не являются взаимно простыми когда их результант равен 0.
не являются взаимно простыми когда их результант равен 0.
Результант 2 многочленов может быть применен не только для установления взаимной простоты многочленов но и для решения других задач например для исключения переменной из системы 2 алгебраических уравнений с 2 неизвестными.
О) Системой из m алгебраических уровней с n переменными называется система:
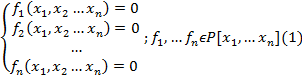
О) Системой 2 алгебраических уравнений с 2 неизвестными называют:
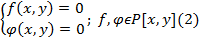
Запишем систему (2) в развернутом виде представив f и 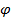 как многочлены от одной переменной x из кольца P[y]
как многочлены от одной переменной x из кольца P[y]
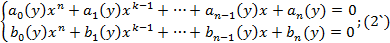
Положив 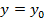 получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0:
получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0: 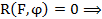
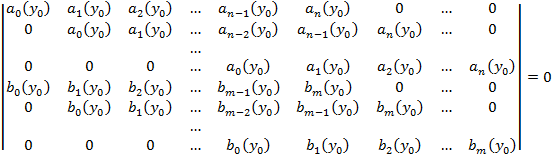
Подставив  в (2’), получаем решение
в (2’), получаем решение 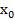 и общее решение
и общее решение 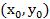 такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.
такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.
Пример 1:
Исключить переменную x и найти решение:
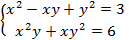
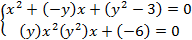


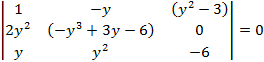
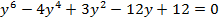
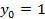
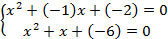

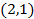
Т3:Многочлены над полем комплексных чисел. Уравнения 3 и 4 степени.
Алгебраические числа.
Л1 02.09.09 Алгебра многочленов
Лит: Винбег Алгебра многочленов
Задачник практикум
Т1: Многочлены от одной переменной



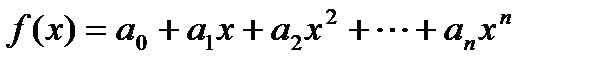 (1) –называется многочленом
(1) –называется многочленом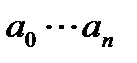 действительные числа, x действительная переменная, n целое число- степень многочлена.
действительные числа, x действительная переменная, n целое число- степень многочлена.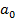 – свободный член.
– свободный член. - 1 степени;
- 1 степени;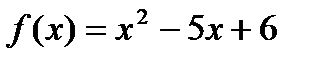 -2 степени;
-2 степени; ;(2)
;(2)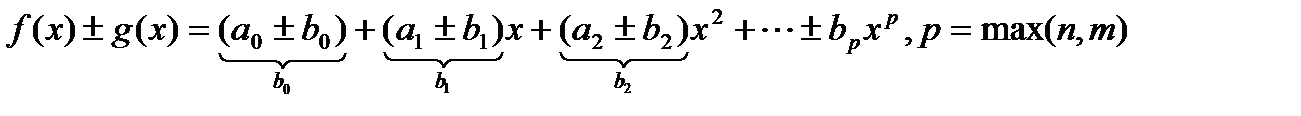 ;
;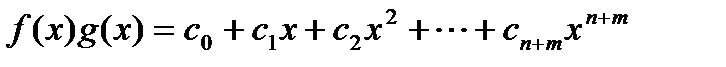 ;
;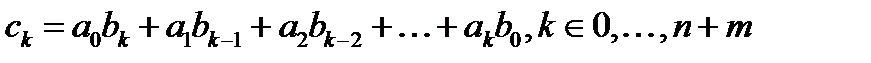
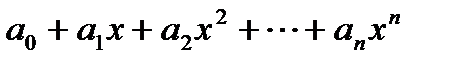 (1)
(1)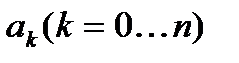 будем называть коэффициентами многочлена (1) при
будем называть коэффициентами многочлена (1) при  , а для всех k>n коэффициент при
, а для всех k>n коэффициент при 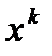 равен 0 для обозначения многочлена используют
равен 0 для обозначения многочлена используют 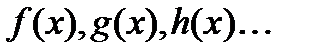 .
.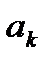 из
из 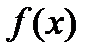 равен соответствующему коэффициенту
равен соответствующему коэффициенту 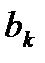 из
из 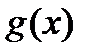 и записывается f(x)=g(x).
и записывается f(x)=g(x).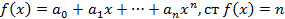
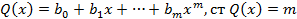
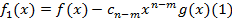 ,
, 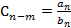
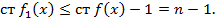 Обозначим
Обозначим 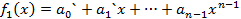 .
.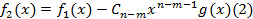 . Где
. Где 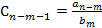 ,
, 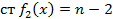 .
.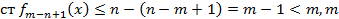 -степень многочлена g(x). Последний многочлен:
-степень многочлена g(x). Последний многочлен: 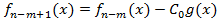 . Почвенное сложение равенств (1) (2) и т.д. дает возможность выразить многочлен f(x) через g(x):
. Почвенное сложение равенств (1) (2) и т.д. дает возможность выразить многочлен f(x) через g(x):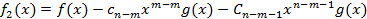
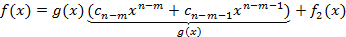
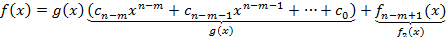
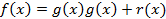
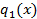 и
и 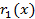 что, выполняется:
что, выполняется: 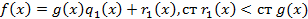 тогда:
тогда: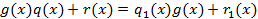
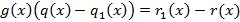
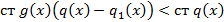
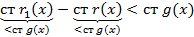
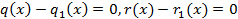
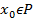 называется корнем k-ой кратности для многочлена
называется корнем k-ой кратности для многочлена 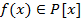 если
если 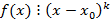 но не делится
но не делится 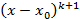 .
.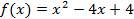
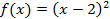
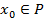 был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие
был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие 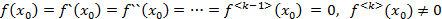 (1)
(1)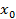 корень k-ой кратности для многочлена
корень k-ой кратности для многочлена 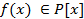 тогда по определению будим иметь
тогда по определению будим иметь 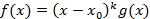 где
где 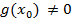 , учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени:
, учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени: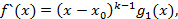 где
где 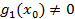 причем
причем 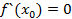 . Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
. Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 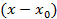 войдет в k-2 степени.
войдет в k-2 степени.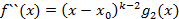 , где
, где 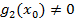 причем
причем 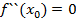 действуя так далее находим
действуя так далее находим 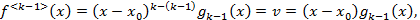 причем
причем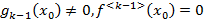
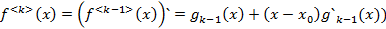 не
не 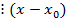 , т.е.
, т.е. 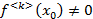 .
.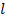 и она отличается от k:
и она отличается от k: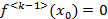
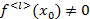 учитывая, что
учитывая, что 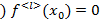 полученные соотношения противоречивы.
полученные соотношения противоречивы.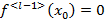
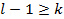
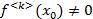
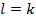 .
.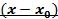
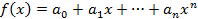
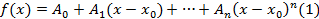 где
где 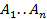 подлежат отысканию. Многочлен в виде (1) продифференцируем n раз:
подлежат отысканию. Многочлен в виде (1) продифференцируем n раз: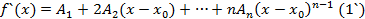
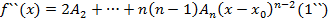
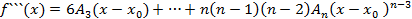

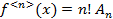
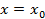 :
: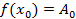
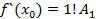
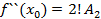
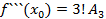
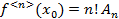
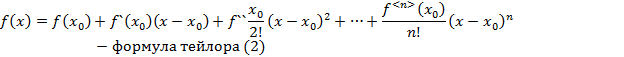
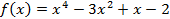 разложить по степеням
разложить по степеням 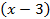 .
.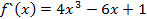
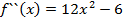
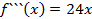
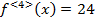
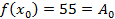
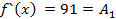
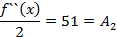
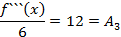
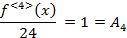
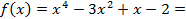
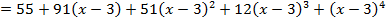
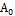
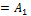
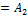
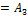
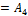
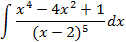
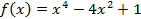
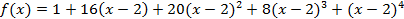
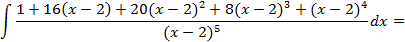
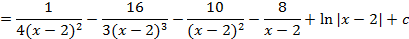
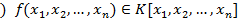 называется симметрическим если он не меняется при любой перестановке входящих в него переменных
называется симметрическим если он не меняется при любой перестановке входящих в него переменных 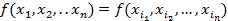 где
где  –перестановка
–перестановка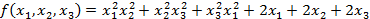 – симметрический
– симметрический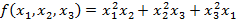 - не симметрический
- не симметрический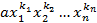 , то он также должен содержать многочлен вида
, то он также должен содержать многочлен вида 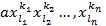 у которых выполнена замена иксов, а индексы образуют перестановку
у которых выполнена замена иксов, а индексы образуют перестановку 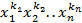 ,
, 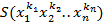 . В частности каждый симметрический многочлен является суммой однородных многочленов
. В частности каждый симметрический многочлен является суммой однородных многочленов
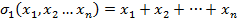
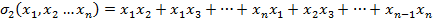
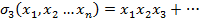
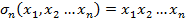
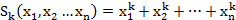
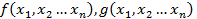 –симметрические
–симметрические 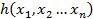 их произведение надо показать что он тоже симметрический
их произведение надо показать что он тоже симметрический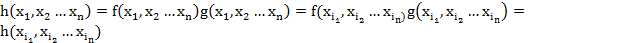 è
è 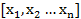 из него можем выделить симметрические. Сами симметрический многочлен тоже образуют кольцо.
из него можем выделить симметрические. Сами симметрический многочлен тоже образуют кольцо.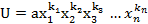 лексико старший член симметрического многочлена
лексико старший член симметрического многочлена  то для последовательности степеней
то для последовательности степеней 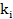 выполняется
выполняется 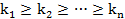 .
. . По условию f симметрический тогда по определению симметрического многочлена он в месте с одночленом U содержит одночлен
. По условию f симметрический тогда по определению симметрического многочлена он в месте с одночленом U содержит одночлен 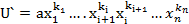 . Исходя из предположения
. Исходя из предположения 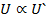 но по условию U старший то есть наше предположение привело к противоречию условию леммы следовательно наше предположение не верно.
но по условию U старший то есть наше предположение привело к противоречию условию леммы следовательно наше предположение не верно.
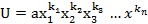 где
где 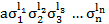 лексикографически старшй член которого совподает c U.
лексикографически старшй член которого совподает c U.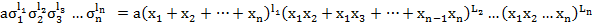
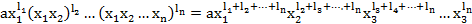
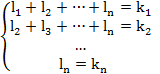 (2)
(2)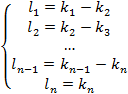 (3)
(3)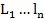 - целые не отрицательные числа а, следовательно могут быть показателями степеней. И так симметрический многочлен:
- целые не отрицательные числа а, следовательно могут быть показателями степеней. И так симметрический многочлен: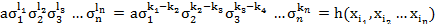

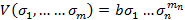
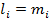 .
.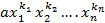 ,тогда по Л2
,тогда по Л2 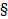 4
4 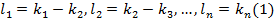 . Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами
. Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами 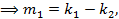 …,
…, 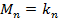 (на основании Т2
(на основании Т2 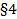 ), из (1),(2) ⟹
), из (1),(2) ⟹ 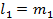 ….
…. 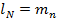 .
.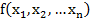 единственным образом представляется в виде многочлена от элементарных симметрических многочленов.
единственным образом представляется в виде многочлена от элементарных симметрических многочленов.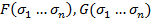
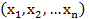 =F
=F 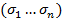
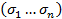 =G
=G  все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 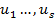 -старшие члены
-старшие члены  . После приведения подобных членов в сумме
. После приведения подобных членов в сумме  если
если 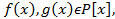
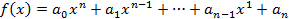
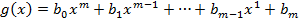
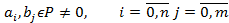

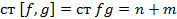 . Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда
. Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда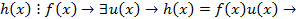

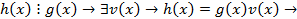
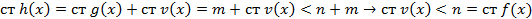
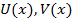 что,
что, 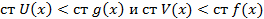 . Выясним когда такие многочлены существуют. Запишем многочлены:
. Выясним когда такие многочлены существуют. Запишем многочлены: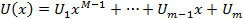
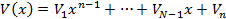
 получим:
получим: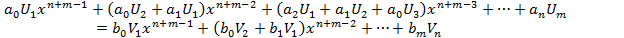
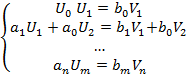
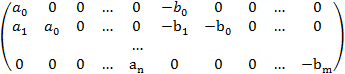
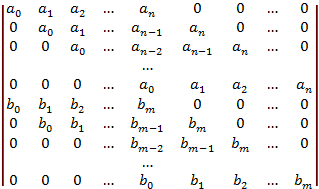
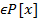 не являются взаимно простыми когда их результант равен 0.
не являются взаимно простыми когда их результант равен 0.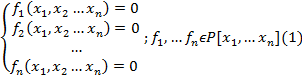
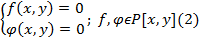
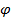 как многочлены от одной переменной x из кольца P[y]
как многочлены от одной переменной x из кольца P[y]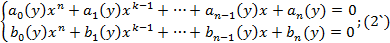
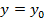 получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0:
получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0: 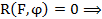
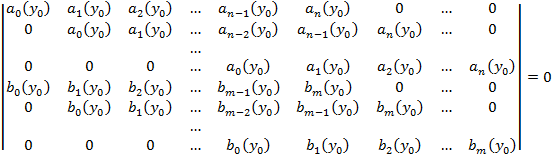
 в (2’), получаем решение
в (2’), получаем решение 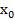 и общее решение
и общее решение 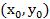 такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.
такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.