http://studopedia.org/1-11225.html
Различают аддитивную и мультипликативную тренд-сезонные модели. Выбор между ними происходит в зависимости от поведения колебания.
Этапы построения аддитивной модели (y=T+S+E):
- выравнивание исходного ВР методом скользящей средней и получение оценок сезонной составляющей путем вычитания из уровней исходного ряда оценок тренда
- расчет сезонных коэф-в усреднением оценок сезонной составляющей по соотв-м сезонам. Проверка условий взаимопогашаемости сезонных колебаний и корректировка сезонных коэф-в в случае необходимости. Формирование сезонной составляющей с использованием сезон коэф-в.
- устранение сезонной компоненты из уровней ВР и получение выровненных данных (T+E). Построение модели тренда по выравненным данным и расчет его значений.
- расчет уровней детерминированной части ВР
- расчет качественных показателей модели и и принятие решений по ней.
При сглаживании уровень относят к середине интервала усреднения, поэтому если длина интервала усреднения четное число, то метки времени исходного и сглаженного рядов будут смещены еще на полпериода. Для устранения этого пары соседних скользящих средних усредняют еще раз и получают центрированные скользящие средние. Условием погашаемости сезонов коэффициентов в случае аддитивной модели гласит, что их сумма должна быть равна нулю. Если это условие не выполняется, то находится коррелирующий коэффициент, т.е. полученную сумму делят на количество сезонов.
Этапы построения мультипликативной модели (y=TSE):
- выравнивание исходного ВР методом скользящей средней с дальнейшим их делением на уровни исходного ряда. В итоге оценка сезонной составляющей
- расчет сезонных коэффициентов по остаткам сезонной составляющей. Проверка условия взаимопогашаемости сезонных коэффициентов. В случае необходимости их корректировка
- формирование сезонной компоненты и ее устранение из уровней исходного ряда (Y/S) и получение выровненных данных
- аналит. уравнение выравнивания полученного ряда и расчет значений тренда по его моделям
- расчет детерминированной части ряда, перемножаем уровни
- расчет качественных показателей и принятие решения по модели
Отличия.
Если временной ряд представляется в виде суммы соответствующих компонент, то полученная модель носит название аддитивной. В общем виде она имеет вид: Y = T+S+E.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Выбор модели осуществляется на основе анализа структурных сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, выбирают аддитивную модель, в которой значения сезонной компоненты предполагаются постоянными для различных циклов.
Если компоненты временного ряда умножаются, то получим мультипликативную модель. Общий вид данной модели следующий: Y = T*S*E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.
Выбор модели осуществляется на основе анализа структурных сезонных колебаний. Если амплитуда сезонных колебаний возрастает иди уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимости от значений сезонной компоненты.
Также аддитивные модели, в отличие от моделей в мультипликативной форме, значительно проще построить, а их параметры оказывается легче рассчитать.
в) рассчитаем отклонения фактических значений от уровней сглаженного ряда:
 ;
;
13. Схема определения интервальных оценок коэффициентов регрессии.
Прогнозирование по уравнению регрессии - подстановка в уравнение регрессии соответственного значения х. Такой прогноз  называется точечным. Он не является точным, поэтому дополняется расчетом стандартной ошибки
называется точечным. Он не является точным, поэтому дополняется расчетом стандартной ошибки  ; получается интервальная оценка прогнозного значения
; получается интервальная оценка прогнозного значения  :
:
Преобразуем уравнение регрессии:

ошибка  зависит от ошибки
зависит от ошибки 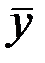 и ошибки коэффициента регрессии
и ошибки коэффициента регрессии  т.е.
т.е. 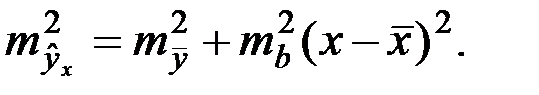





 ;
; называется точечным. Он не является точным, поэтому дополняется расчетом стандартной ошибки
называется точечным. Он не является точным, поэтому дополняется расчетом стандартной ошибки  :
:

 зависит от ошибки
зависит от ошибки 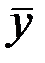 и ошибки коэффициента регрессии
и ошибки коэффициента регрессии  т.е.
т.е.