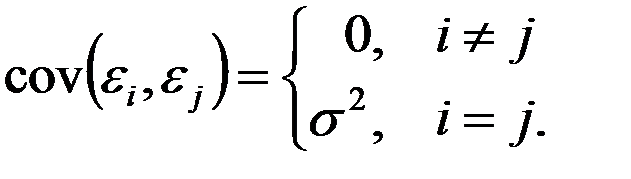Простейшая структурная форма модели имеет вид:
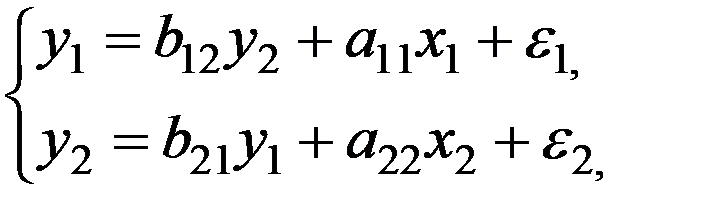
где y1, y2 – эндогенные переменные, x1, x2 – экзогенные.
Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной.
Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма преобразуется в приведенную.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
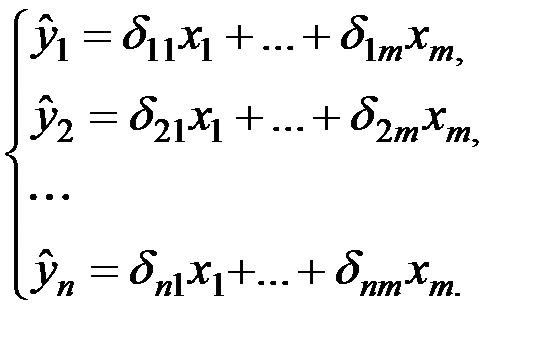
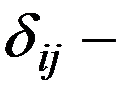 коэффициенты приведенной формы модели.
коэффициенты приведенной формы модели.
Применяя МНК, можно оценить 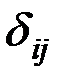 , а затем оценить значения эндогенных переменных через экзогенные.
, а затем оценить значения эндогенных переменных через экзогенные.
Приведенная форма позволяет выразить значения эндогенных переменных через экзогенные, однако аналитически уступает структурной форме модели, т.к. в ней отсутствуют оценки взаимосвязи между эндогенными переменными.
5. Суть метода наименьших квадратов. Предпосылки МНК. Каковы последствия их выполнимости или невыполнимости?
МНК - метод оценивания неизвестных параметров уравнения регрессии.
Суть МНК заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 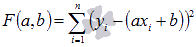 принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
Для получения по МНК наилучших результатов необходимо выполнение следующих предпосылок:
10. Математическое ожидание случайного отклонения равно нулю для всех наблюдений: 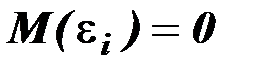 .
.
20.Дисперсия случайных отклонений постоянна:. 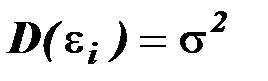
Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсии отклонений)
30. Случайные отклонения εi и εj являются независимыми друг от друга для 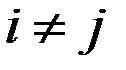 :
:
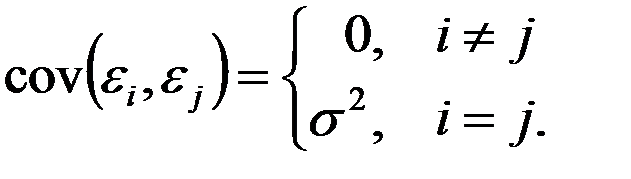
Выполнимость этого условия называется отсутствиемавтокорреляции.
40. Случайное отклонение должно быть независимо от объясняющих переменных.Обычно это условие выполняется автоматически, если объясняющие переменные в данной модели не являются случайными. Кроме того, выполнимость данной предпосылки для эконометрических моделей не столь критична по сравнению с первыми тремя.
Если перечисленные четыре условия выполняются, то оценки, сделанные с помощью МНК, являются наилучшими оценками, так как они обладают свойствами:
1) несмещенности, что означает отсутствие систематической ошибки в положении линии регрессии;
2) эффективности – имеют наименьшую дисперсию в классе всех линейных несмещенных оценок;
3) состоятельности – при достаточно большом объеме данных оценки приближаются к истинным значениям.





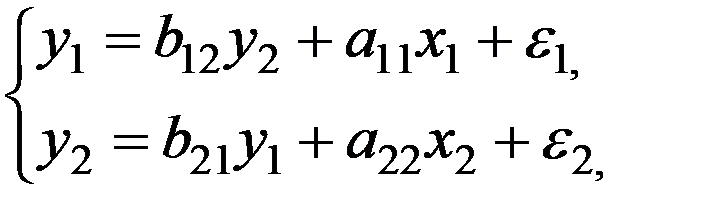
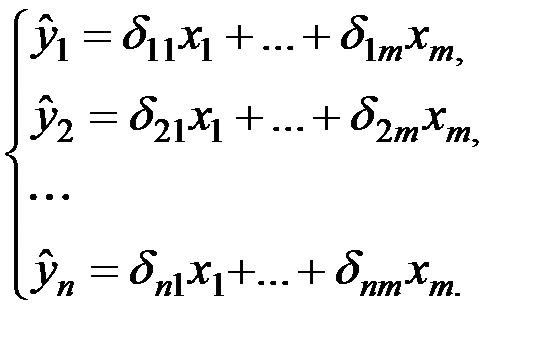
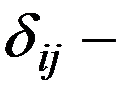 коэффициенты приведенной формы модели.
коэффициенты приведенной формы модели.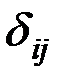 , а затем оценить значения эндогенных переменных через экзогенные.
, а затем оценить значения эндогенных переменных через экзогенные.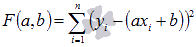 принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.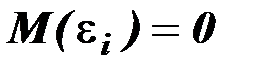 .
.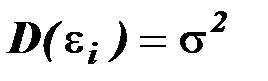
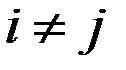 :
: