Виды задач линейного программирования (ЗПЛ)

Геометрическая интерпретация и графический метод решения ЗЛП.

Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения.

 

Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать ЗЛП.

2. Построить на плоскости {х1, х2} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c₁x₁ + c₂x₂ = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

Z= 2x1 + 4x2 → max;

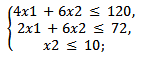
x1 ≥ 0, x2 ≥ 0.

2. Теперь построим прямые, соответствующие каждому из функциональных ограничений задачи. Эти прямые обозначены на рисунке (1), (2) и (3).

 

3. Штрихи на прямых указывают полуплоскости, определяемые ограничениями задачи.

4. Область допустимых решений включает в себя точки, для которых выполняются все ограничения задачи. В данном случае область представляет собой пятиугольник ABCDO.

5. Прямая, соответствующая целевой функции, на рисунке представлена пунктирной линией.

6. Прямую передвигаем параллельно самой себе вверх (направление указано стрелкой), поскольку именно при движении в этом направлении значение целевой функции увеличивается. Последней точкой многоугольника решений, с которой соприкоснется передвигаемая прямая, прежде чем покинет его, является точка C. Это и есть точка, соответствующая оптимальному решению задачи.

7. Осталось вычислить координаты точки С. Она является точкой пересечения прямых (1) и (2). Решив совместно уравнения этих прямых, найдем:x₁ = 24, x₂=4..Подставляя найденные величины в целевую функцию, найдем ее значение в оптимальной точке Z=64.

Постановка и экономико-математическая модель задачи о назначениях

9. Задача производственного планирования как задача об оптимальных назначениях

Базовая модель задачи планирования производства.

Математические модели дискретного программирования

 

Градиентный метод

Градиентом непрерывной однозначной функции j (обозначается gradj или Ñj) называется вектор

,

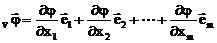где 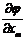– частная производная функции по m-му параметру xm, 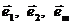– единичные векторы в направлении координатных осей.

Градиент функции Ñjпредставляет собой вектор перпендикулярный к

контуру поверхности j в пространстве параметров, который указывает направление наибольшего возрастания j в данной точке. Противоположный вектор задает направление наискорейшего спуска (рис. 2.3.1). Изменяя в функции отклика независимые переменные пропорционально величинам коэффициента регрессии, будем двигаться в направлении градиента функции отклика по самому крутому пути. Поэтому процедура движения называется "крутым восхождением". Величины составляющих градиента определяются формой поверхности отклика, начальной (нулевой) точкой 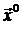и интервалами варьирования.

Длина вектора Ñj определяется по формуле:

(2.3.1)

Движение по градиенту осуществляется в следующем порядке:

1. Вычисляются составляющие вектора 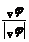в точке 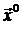(основной уровень): .

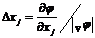2. Последовательно прибавляют составляющие к основному уровню факторов: 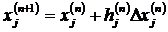, где h_j– шаг движения.

3. Итерационный процесс заканчивается, когда выполняется неравенство: 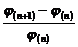<e

Шаг движения по градиенту выбирается из следующих соображений. Небольшой шаг потребует значительного числа опытов при движении к оптимуму. Большой шаг увеличивает вероятность проскакивания области оптимума. Нижняя граница шага ограничена возможностью фиксирования двух соседних опытов, а верхняя – областью определения фактора.

Функция, величины коэффициентов которой различаются несущественно, называется симметричной относительно коэффициентов. Движение по градиенту наиболее эффективно для симметричной функции. Движение по градиенту считается эффективным, если реализация опытов приводит к улучшению значения целевой функции.

Градиентный метод оптимизации не решает вопроса о самой лучшей точке поверхности отклика при наличии нескольких экстремальных точек.

 

Рис. 2.3.1. Градиент функции Ñj в точке А.

Первая теорема подобия

План полного факторного эксперимента

Планирование эксперимента – процедура выбора количества экспериментов и условий их проведения, необходимых для решения поставленной задачи с требуемой точностью.

Факторами называются величины, которые экспериментатор изменяет по своему усмотрению. Факторы – вектора.

Полным факторным экспериментом называется эксперимент, при котором реализуются все возможные сочетания уровней варьирования.

Свойства полного факторного плана эксперимента.

1. Симметричность относительно центра эксперимента: Алгебраическая сумма элементов вектора столбца каждого фактора равна нулю.

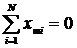
2. Ортогональность матрицы планирования: Сумма произведений элементов любых двух векторных столбцов равна нулю.

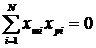
3. Условие нормировки: Сумма квадратов элементов столбца каждого фактора равна количеству опытов.

4. Точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления

9. Классификация планов эксперимента

Планирование эксперимента – процедура выбора количества экспериментов и условий их проведения, необходимых для решения поставленной задачи с требуемой точностью.

Факторами называются величины, которые экспериментатор изменяет по своему усмотрению. Факторы – вектора.

I=F^T∙F – информационная матрица плана [x]. C=I^-1 – ковариационная матрица плана [x]/

План эксперимента называется ортогональным, если информационная матрица диагональная

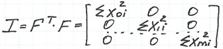
Ортогональные планы используются, когда точный вид модели неизвестен и исследователь использует данные для отбора переменных, которые существенно влияют на выходную величину.

План называется центральным, если его центр расположен в начале координат.

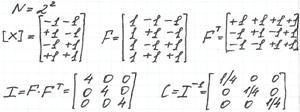
Матрица I – диагональная => план ортогональный.

Композитностью плана называется свойство плана, позволяющее разделить эксперимент на несколько этапов и постепенно переходить от простых моделей к более сложным, используя предыдущие наблюдения.

Насыщенность плана – связь между количеством факторов М и опытов N, если N<M, то нельзя найти ед. значения коэффициентов модели [a_e].

Критерий оптимальности плана.

1-я группа – следит за точностью экспериментов модели. [a_e] – оценивает точность коэффициентов модели. D, A, E – оптимальность.

2-я группа – оценивает точность предсказания по модели η. G, Q – оптимальность.

3-я группа – связана со стратегией эксперимента

Коэффициенты модели случайной величины имеют доверительный интервал.

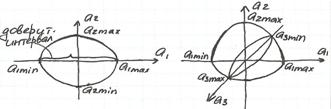
D – оптимальные планы – называются планы, которые соответствуют min определителю по ковариационной матрице.

С=I^-1=(F^T∙F)^-1

min|c|

Определитель ковариационной матрицы пропорционален объему эллипсоида рассеивания коэф. модели.

А – оптимальные планы – это планы, которым соответствует минимальный след ковариационной матрицы.

(след): SpurC=С₁₁+С₂₂+С₃₃+С_LL

А – оптимальные планы обеспечивают минимум средней дисперсии коэффициентов модели.

Е – оптимальный план – соответствует собственному значению ковариационной матрицы.

λ – собственное значение матрицы С. Система уравнений С∙x, в этой системе матрицу можно заменить числом, расположенным по диагонали – это собственное значение матрицы.

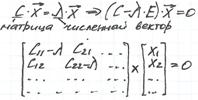
Е – оптимальные планы не позволяют дисперсиям отдельных коэффициентов моделей иметь недопустимо большие размеры.

G – оптимальные планы – минимизируют максимально возможную дисперсию предсказания от модели: min (maxD(η)). Эти планы гарантируют, что в области эксперимента нет точек, которые имеют низкую точность вычисления по модели.

Q – оптимальные планы – минимизируют среднюю дисперсию предсказания. minD_cp(η), D_cp – средняя дисперсия.

Построить планы, удовлетворяющие одновременно нескольким критериям оптимальности можно только для простых моделей, поэтому используют планы, построенные на компромиссном решении, близкие к оптимальным планам по разным критериям. Такие планы называются робастные планы.

е^(D), е^(A), е^(E), е^(Q) и т.д. – коэффициенты. Чем ближе произв. план к оптимальному оценивают коэффициенты е.

10. Критерии оптимальности планов эксперимента.

11. Построение линейных и квазилинейных уравнений регрессии на базе планирования эксперимента

Требования к технологическому процессу, к технологичности заготовок, к конструкции штампов и оборудованию при создании автоматизированных производств.

3.1 Автоматизировать надо не всякую технологию, а ту, которая отвечает следующим требованиям:

1. Устойчивость. Устойчивый тех. процесс – такой процесс, при котором гарантируется получение качественных деталей по чертежу (без брака) при условии, что допускаемые отклонения свойств материала (σ_Т, σ_В, пластичность), формы и размеры заготовки (D±ΔD, t±Δt), режимы работы технологического агрегата и т.п. находятся в пределах допусков, оговоренных в ГОСТ, РТМ или ТУ. (РТМ – рекомендованные технические материалы)

2. Интенсивность. Интенсивный тех. процесс – процесс, при котором максимально используются возможности обрабатываемого материла (пластичность), возможности оборудования, инструмента и др. С целью обеспечения минимального количества переходов и операций для получения детали. Достигается с помощью: увеличения возможной степени деформации, объединение некоторых операций в одном агрегате (нагрев и деформацию).

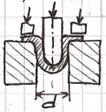Пример: обычная вытяжка. k_в=1,4-1,7; k_в=D/d

Интенсивная вытяжка (с нагревом фланца, с подпором фланца). k_в=1,6-2,2

3. Поточность производства – т.е. расположение тех. операций в одном направлении, исключающем обратное движение заготовки.

Пример: ГОШ (1-осадка, 2-предварительная штамповка, 3-окончательная).

4. Концентрация операций в одном технологическом агрегате

Пример: многопозиционные штампы, прессы для изготовления колец подшипников

5. Групповая технология – это группировка

деталей по общим технологическим признакам (температура, форма, размеры и т.д.).

3.2) заготовки должны отвечать требованию технологичности по загрузке

А) бункеруемые (не повреждающиеся при механическом или другом воздействии, не сцепляющиеся друг с другом, имеющие геометрические параметры для легкой ориентации)

Б) небункеруемые (нежесткие, крупногабаритные, недостаточно прочные, взаимосопрягающиеся, …)

2) технологичность по типизации и унификации

Применение групповых тех. Процессов позволяет использовать быстропереналаживающие загрузочные устройства.

3) технологичность по стабильности и уровню продукции

- ужесточение технологических допусков на отклонения размеров и форы

- требования к качеству поверхности

4) при проектировании автоматизированных процессов заготовки, полуфабрикаты должны иметь для лучшего ориентирования:

- max плоскостей и осей симметрии

- ярко выраженные «ключи ориентирования» (канавки, выступы, фаски и т.д.)

Рис. 11. Направление перемещения изделия в штампе, по­казанном на рис. 10

3.3 Требования, предъявляемые автоматизацией к технологическому процессу, обусловливают конструкцию инструмента для автоматизированных технологических процессов, которая должна быть увязана с механизирующими устройствами и не должна затруднять их применение. Устойчивость процесса, концентрация операций, технологичность изделий — все это также неразрывно связано с конструированием штамповой оснастки. Следует помнить, что простота и надежность средств автоматизации в первую очередь зависит от соответствия штампов условиям работы со средствами автоматизации.

На рис. 10 был показан закрытый штамп с противодавлением, установленный в кузнечном цехе МЗМА, для штамповки шестерни. Выше отмечалось, что данный процесс значительно облегчает проблему автоматизации, так как удовлетворяет основным требованиям, предъявляемым автоматизацией к технологическим про­цессам. Однако автоматизировать штамп, показанный на рис. 10, практически невозможно. В штампе три перехода: фигурная осадка, штамповка и просечка дна. Расположение ручьев и их уровень выбраны произвольно. Более того, для закладки изделия в последний ручей необходимо проделать сложный маневр по обходу стоек прижима, т. е. для автоматизации указанного штампа (см. рис. 10) необходимо создать устройство, которое бы осуществляло сложные манипуляции с заготовкой (рис. 11). Даже если оно и будет создано, то из-за различных уровней расположения ручьев (плоскости А_г, Л₂, А₃, Л₄) и шага подачи (а_г ф а_г ф а₃) оно получится настолько сложным, что трудно будет добиться надежной его работы. Этот пример показывает, что конструкция инструмента может затруднить проблему автоматизации процесса.

При автоматизации технологических процессов ковки и штамповки работа средств автоматизации и пресса частично совмещается. Чтобы избежать попадания частей средств автоматизации под штамп, в них должны быть предусмотрены специальные блокировочные устройства, обеспечивающие аварийный принуди­тельный отвод захватного органа из опасной зоны. В последнее время начали применяться специальные устройства, встраиваемые в штамп и контролирующие наличие и положение изделия в нем. Эти устройства будут рассмотрены ниже.

Классификация захватных устройств. Принципы выбора и расчета захватных устройств. Пример метода расчета.

Проектирование САМ начинается с выбора захватного органа, в функции которого входит: захват, удержание и освобождение детали.

Классификация:

А) С регулируемым усилием захвата: 1) Фрикционный; 2) Клещевой (НМ, Ш); 3) Пневматический (Ш, Пл); 4) Электромагнитный (Ш).

Б) С нерегулируемым усилием захвата: 1) Фрикционный (НМ); 2) Клиновой (НМ): роликовый, шариковый, эксцентриковый, цанговый; 3) Ножевой (НМ); 4) Крючковый (НМ, Ш); 5) Толкающий (Ш): шиберный, планочный, дисковый; 6) Пневматический (Ш); 7) Карманчиковый (Ш, О); 8) «Гравитационный» (Ш).

(НМ – непрерывный материал, Ш – штучная заготовка, О – объемная заготовка (стакан), Пл – плоская заготовка).

Выбор ЗУ. Захватное устройство реализует захват объекта, используя информацию о его положении и размерах. Конструкция захватного устройства должна выбираться, исходя из обеспечения наиболее широкого диапазона возможности захвата предметов различных форм и размеров. Выбор захватного устройства начинают после выбора объекта роботизации: 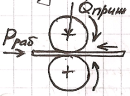Фрикционный захват (пример: валковая подача). Захват осуществляется за счет сил трения и, как правило, применяется для непрерывных заготовок (лента, лист).

Необходим прижим Q.

Q=P/μ – для 1-го приводного валка. Q=P/2μ – для 2-х приводных валков.

Общий случай: Q=β∙(P/zμ), где z – количество приводных валков; β=1,5-2 – коэффициент надежности; μ=0,08-0,12

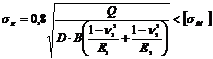Усилие Q прижима проверяется по условию смятия (по формуле Герце-Беллева): (σ_k)

ν, E – коэффициенты Пуассона и модули упругости заготовки и валка. [σ_см]≈2σ_S. Приσ_К>[σ_см] устанавливается несколько приводных валков.

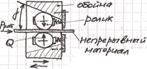←Клиновой захват. Является тоже фрикционным, но нерегулируемый. Наиболее распространенный –роликовый. Условие заклинивания ленты и перемещения: tgα<tgγ=μ=0,1; γ≤12º; Q=P/tgγ

 

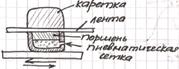Клещевой захват. Пример: для непрерывного материала.

при подаче давления из пневмосети поршень зажимает ленту и каретка перемещает ее на заданное расстояние.

Q=β∙(P/2μ), где Р – рабочее усилие, Q – усилие зажима ленты, β=1,3-1,6; μ=0,1-0,12

Пневматический захват. Осуществляется за счет перепада давления в атмосфере и полости захвата. Различают 1) пассивные (неуправляемые) захваты – применяются редко т.к. ненадежны, можно в комбинации с другими, например: с э/м захватом; 2) управляемые.

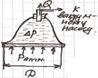←а) Q – усилие подъема

Q=1/β∙Δp∙F,

где F=πD²/4; β=1,2-1,3; D – расчетный диаметр захвата

 

 

б) l≠0; G – вес заготовки;n≥G/Q – число захватов. Q=1/βk∙ Δp∙F; k=1+4l/D

 

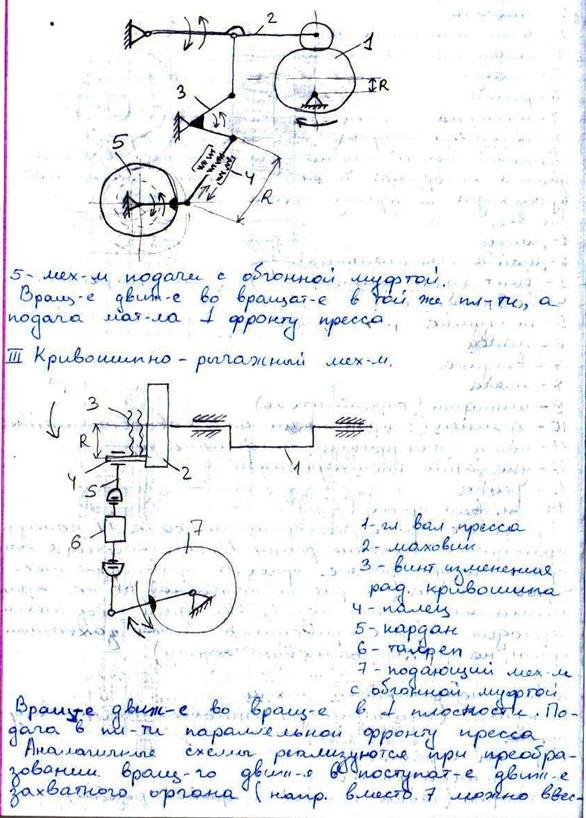
Составные преобразующие механизмы. Принципы выбора и расчета. Примеры.

 

Виды задач линейного программирования (ЗПЛ)

Методы линейного программирования используют в прогнозных расчетах, при планировании и организации производственных процессов. Линейное программирование – это область математики, в которой изучаются методы исследования и отыскания экстремальных значений некоторой линейной функции, на аргументы которой наложены линейные ограничения.

Такая линейная функция называется целевой, а набор количественных соотношений между переменными, выражающих определенные требования экономической задачи в виде уравнений или неравенств, называется системой ограничений. Слово программирование введено в связи с тем, что неизвестные переменные обычно определяют программу или план работы некоторого субъекта.

Совокупность соотношений, содержащих целевую функцию и ограничения на ее аргументы, называют математической моделью задачи оптимизации.

ЗЛП записывается в общем виде так:

Здесьмx_j-неизвестные, a_ij, b_i, c_j-заданные постоянные величины.Ограничения могут быть заданы уравнениями.Наиболее часто встречаются задачи в виде: имеетсяn ресурсов приmограничениях. Нужно определить объемы этих ресурсов, при которых целевая функция будет достигать максимума (минимума), т. е. найти оптимальное распределение ограниченных ресурсов. При этом имеются естественные ограничения x_j>0.

При этом экстремум целевой функции ищется на допустимом множестве решений, определяемом системой ограничений, причем все или некоторые неравенства в системе ограничений могут быть записаны в виде уравнений.

Для составления математической модели ЗЛП необходимо:

1)обозначить переменные;

2)составить целевую функцию;

3)записать систему ограничений в соответствии с целью задачи;

4)записать систему ограничений с учетом имеющихся в условии задачи показателей.

Если все ограничения задачи заданы уравнениями, то модель такого вида называется канонической. Если хоть одно из ограничений дано неравенством, то модель неканоническая.

Примеры задач, которые сводятся к ЗПЛ.

1. задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии (задача об ассортименте);

2. задача на максимум выпуска продукции при заданном ассортименте;

3. задача о смесях (рационе, диете и т.д.);

4. транспортная задача;

5. задача о рациональном использовании имеющихся мощностей;

6. задача о назначениях.

1.Задача оптимального распределения ресурсов.

Предположим, что предприятие выпускает различных nизделий. Для их производства требуется m различных видов ресурсов (сырья, рабочего и машинного времени, вспомогательных материалов). Эти ресурсы ограничены и составляют в планируемый период b_i, b₂,..., b_mусловных

единиц. Известны также технологические коэффициенты a_ij,, которые указывают, сколько единиц i-го ресурса требуется для производства изделия j-го вида. Пусть прибыль, получаемая предприятием при реализации единицы изделия j-го вида, равна c_j. В планируемый период все показателиa_ij, b_i, c_j предполагаются постоянными.

Требуется составить такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей.

Экономико-математическая модель задачи:

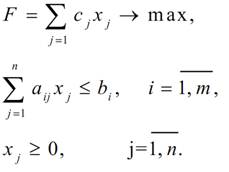
Целевая функция представляет собой суммарную прибыль от реализации выпускаемой продукции всех видов. В данной модели задачи оптимизация возможна за счет выбора наиболее выгодных видов продукции. Ограничения означают, что для любого из ресурсов его суммарный расход напроизводство всех видов продукции не превосходит его запасы.

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

2. Основные определения ЗЛП

Опр.1. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

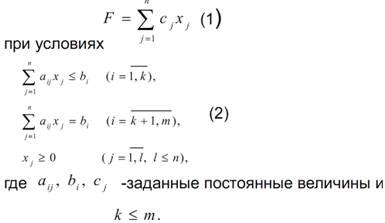
Опр.2. Функция (1) называется целевой, а условия (2)-ограничениями задачи.

Опр.3. Совокупность чисел ,удовлетворяющих ограничениям задачи (1)-(2), называются допустимым решением (или планом).

Опр.4. Основной, или канонической ЗЛП называется задача, состоящая в определении значения целевой функции

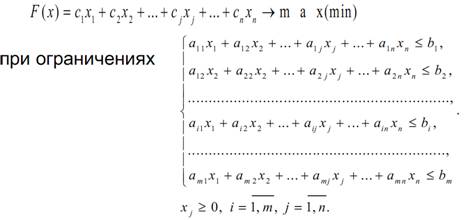
Если требуется для удобства или по смыслу задачи перейти от одной формы записи к другой, то поступают следующим образом. Если требуется найти минимум функции, то можно перейти к нахождению максимума, умножив целевую функции на (-1).Ограничение –неравенство вида ≤ можно преобразовать в равенство добавлением к его левой части неотрицательной дополнительной переменной, а ограничение неравенство вида ≥- в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной.

План называется опорным, если все компоненты базисного решения системы ограничений канонической задачи линейного программирования неотрицательны. Число положительных компонент опорного плана не может быть больше m, т.е.числа уравнений в ограничениях.

Опорный план называется невырожденным, если он содержит m положительных компонент. В противном случае он называется вырожденным.План, при котором целевая функция ЗЛП принимает свое максимальное (минимальное) значение, называется оптимальным.